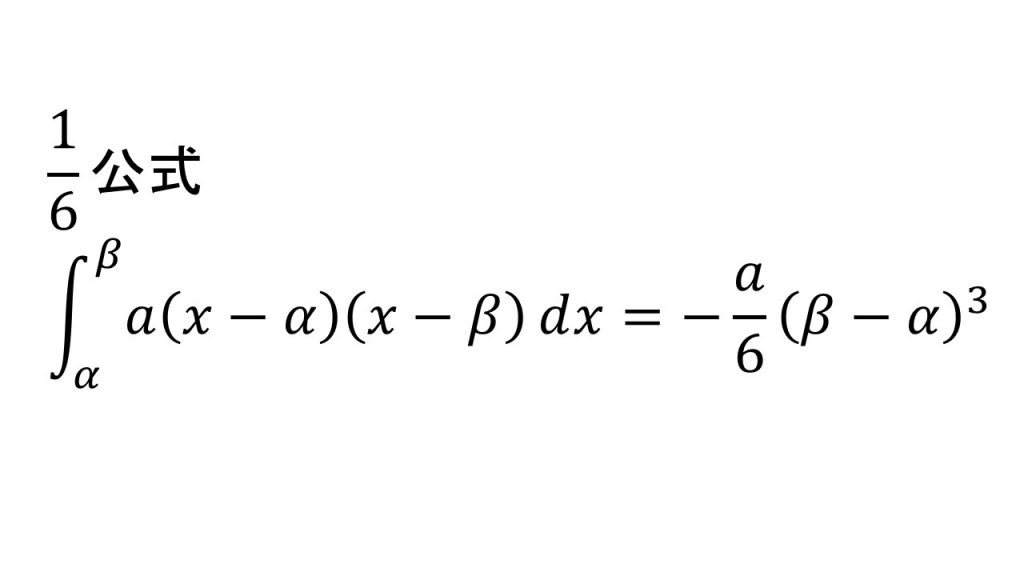(1)式と証明
①二項定理


②相加平均・相乗平均の大小関係

※(a+b)/2のことを相加平均、√abのことを相乗平均という。
(2)複素数と方程式
①解と係数の関係

②剰余の定理:整式P(x)を1次式x-aで割ったときの余りはP(a)
③因数定理:1次式x-aが整式P(x)の因数である⇔P(a)=0

④知っておきたい式変形
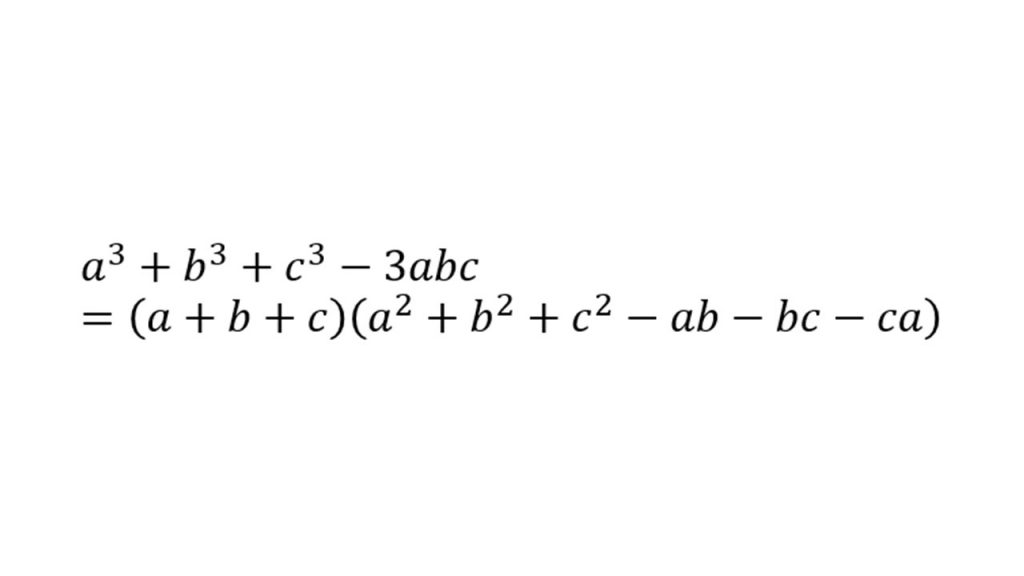
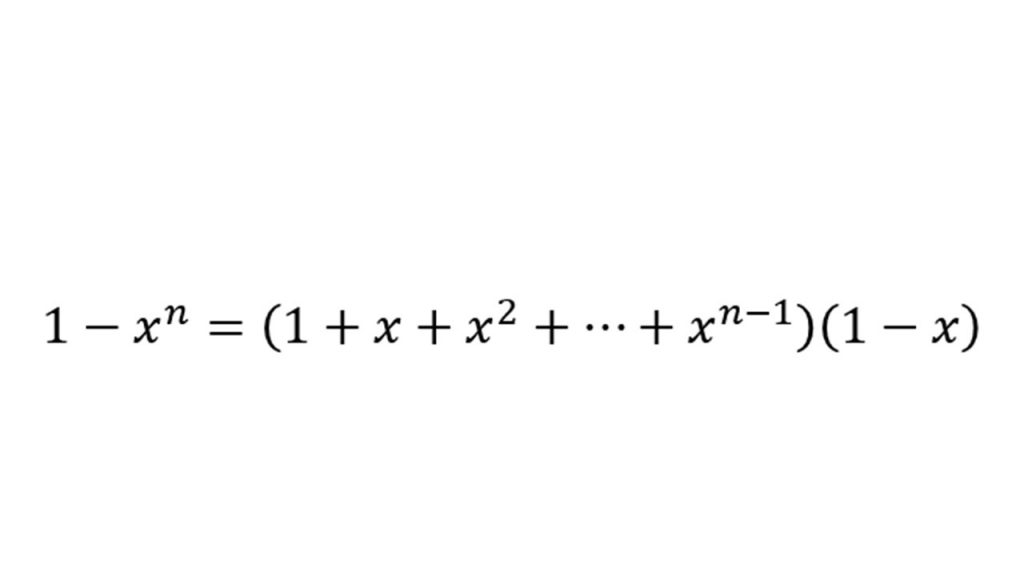
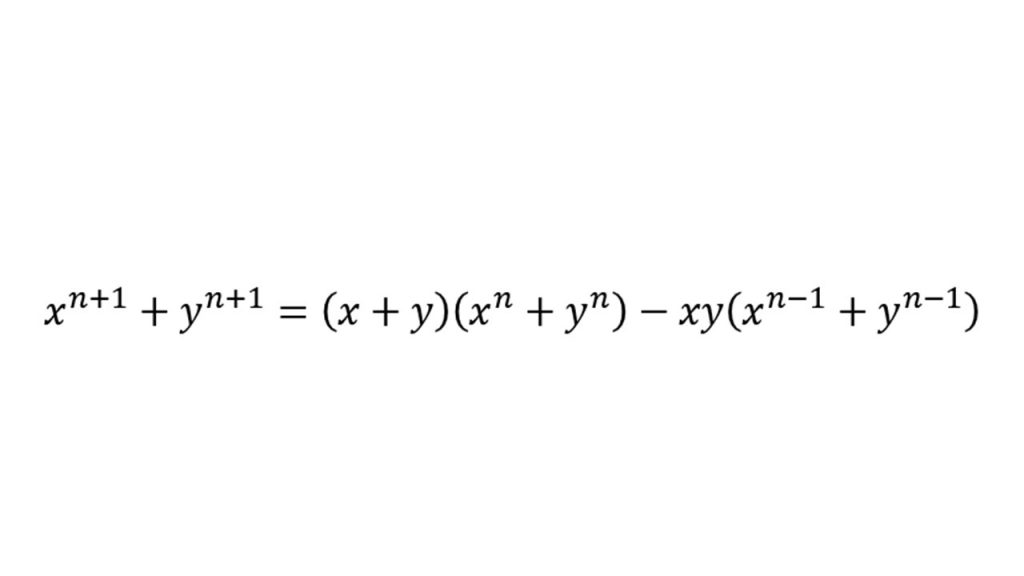
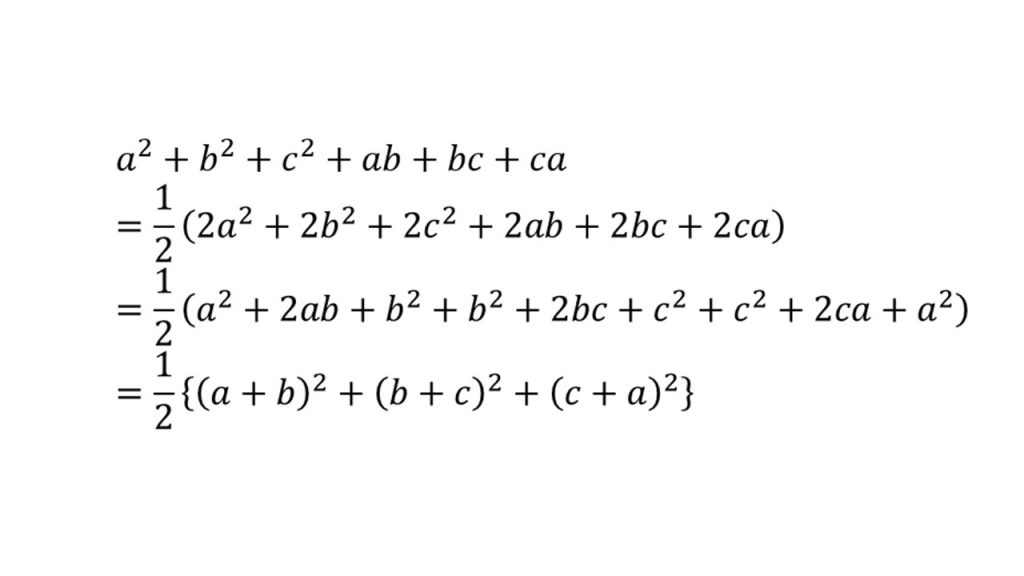
(3)図形と方程式(点と直線)
①2点間の距離
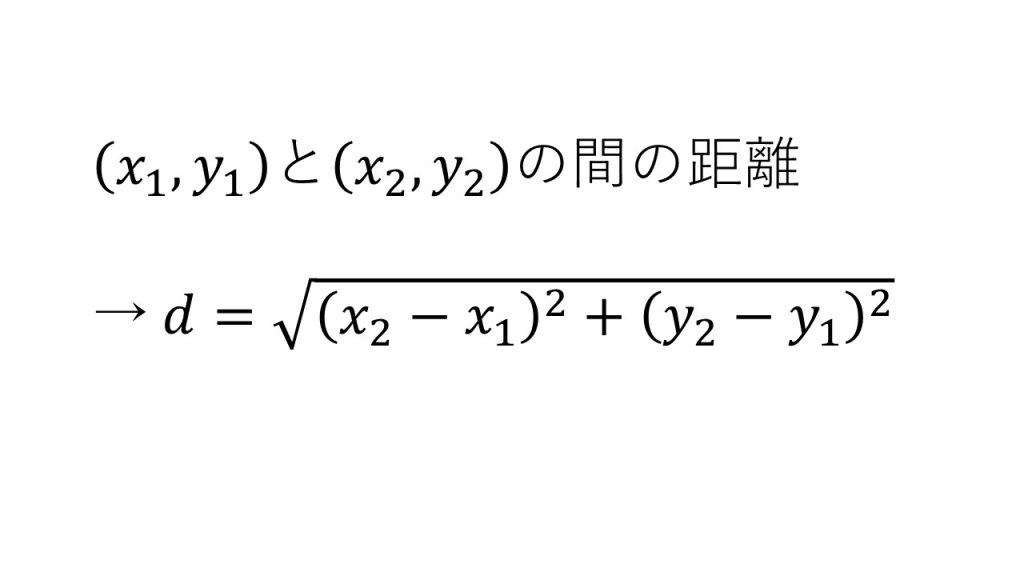
②中点

③内分点
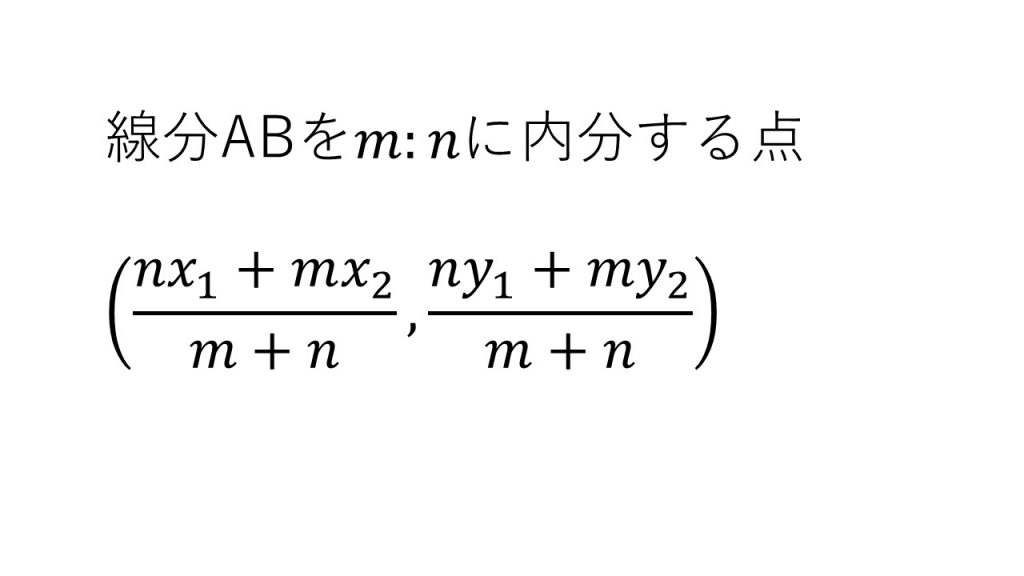
④外分点

⑤重心

⑥直線の方程式

※直線の方程式は、ⅰ)傾きとⅱ)通る点の2つが分かれば求められる。
⑦2直線が平行
傾きが一致する ⇔ m=m’
⑧2直線が垂直
傾きの積が-1 ⇔ m・m’=-1
⑨点と直線の距離
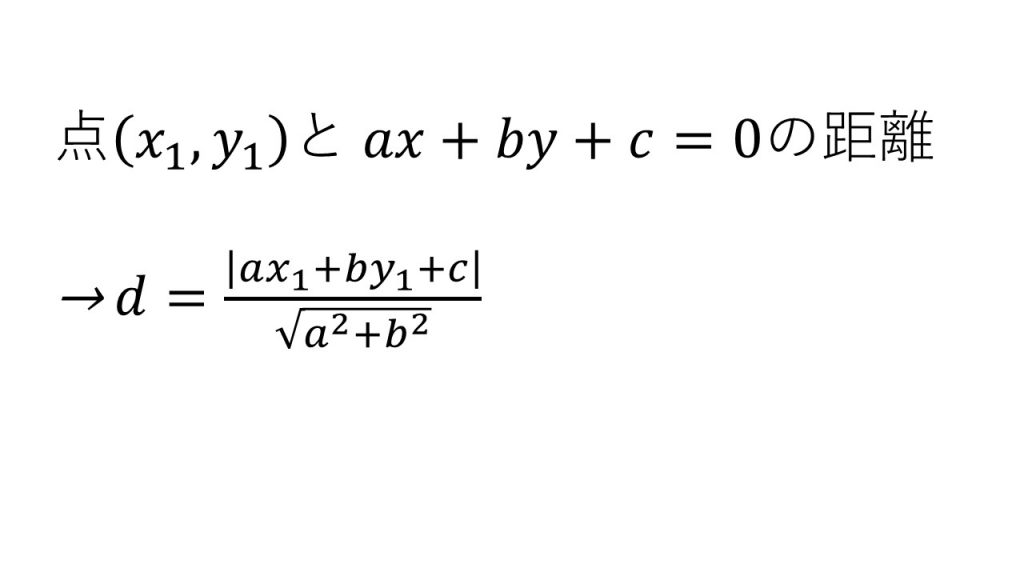
※点と直線の距離を求めるときは、直線の方程式をax+by+c=0の形に変形しよう。
⑩直線に対称な点
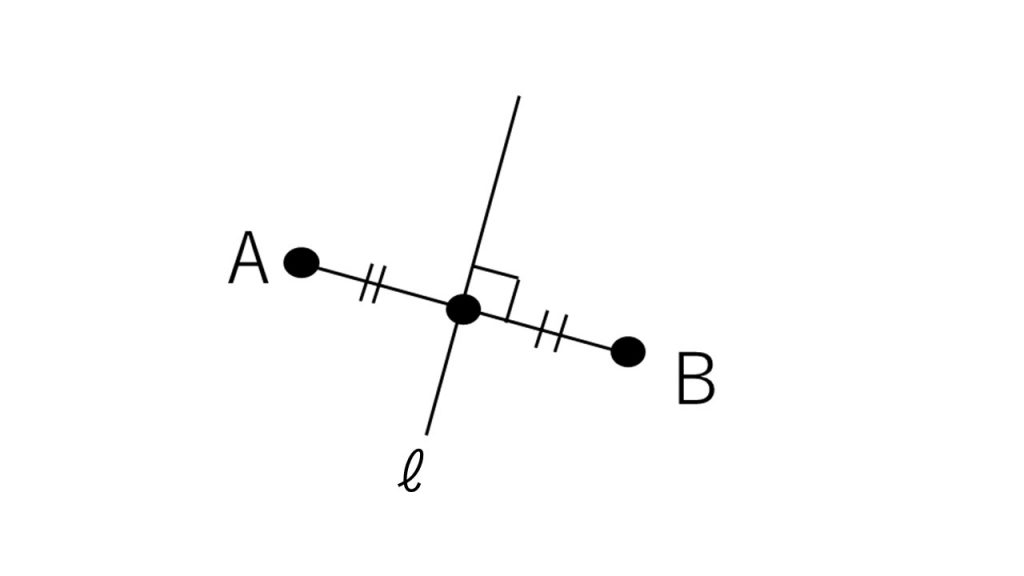
☆点Aと点Bが直線ℓに関して対称なとき
ⅰ)ABの中点がℓ上にある
ⅱ)ABとℓが垂直 ⇔ (ABの傾き)・(ℓの傾き)=-1
(4)図形と方程式(円)
①円の方程式


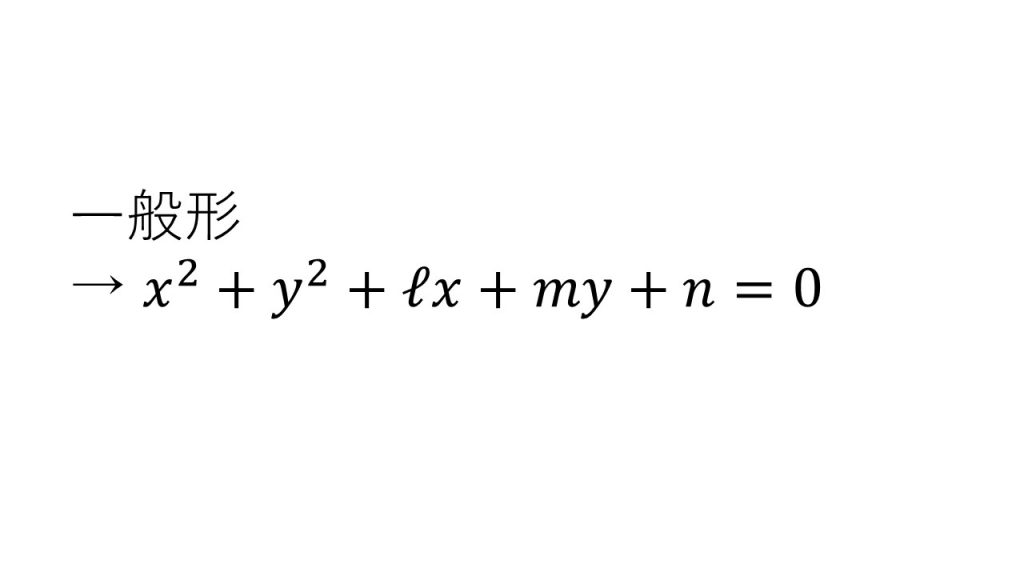
②円と直線の共有点の個数
☆求める手順1
ⅰ)円の方程式と直線の方程式を連立させる。
ⅱ)ⅰ)でyを消去すればxの二次方程式となるので、その二次方程式の判別式Dを利用する。
ⅲ)D>0 ⇔ 共有点2個
D=0 ⇔ 共有点1個(接する)
D<0 ⇔ 共有点0個
☆求める手順2
ⅰ)円の中心と直線の距離dを求める。
ⅱ)dと半径rの関係を調べる。
ⅲ)d<r ⇔ 共有点2個
d=r ⇔ 共有点1個(接する)
d>r ⇔ 共有点0個
③円の接線の公式


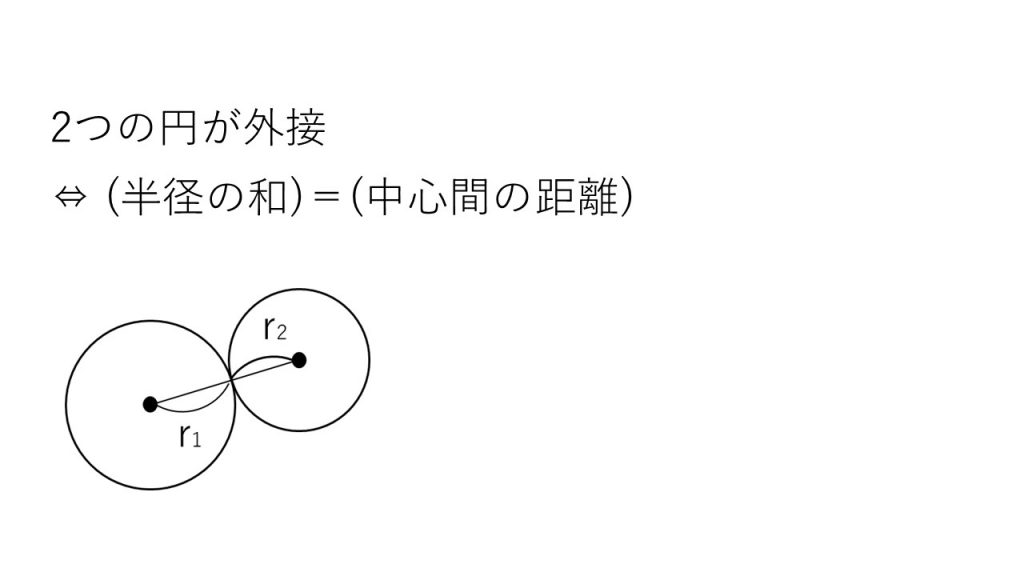
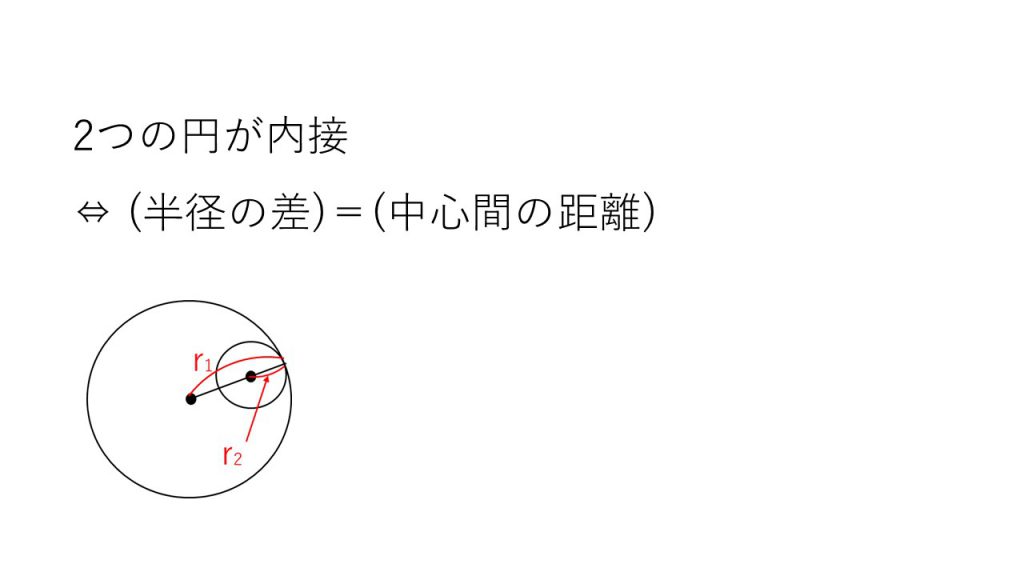
④2つの円の位置関係
⑤2曲線の交点を通る曲線の方程式:kf(x, y)+g(x, y)=0
→2曲線の交点を通る曲線の方程式kf(x, y)+g(x, y)=0の使い方と原理解説授業
(5)三角関数
①弧度法

※θの単位はrad(ラジアン)
②おうぎ形の面積

※θの単位はrad(ラジアン)
③三角関数の性質(θ+2π、-θ、π+θ、π-θ、π/2+θ、π/2-θ)
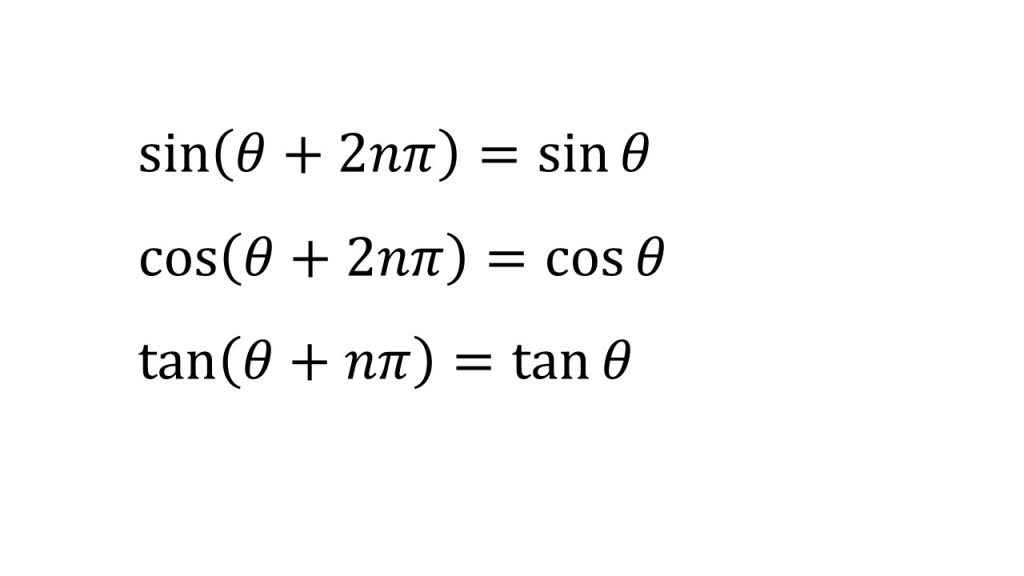
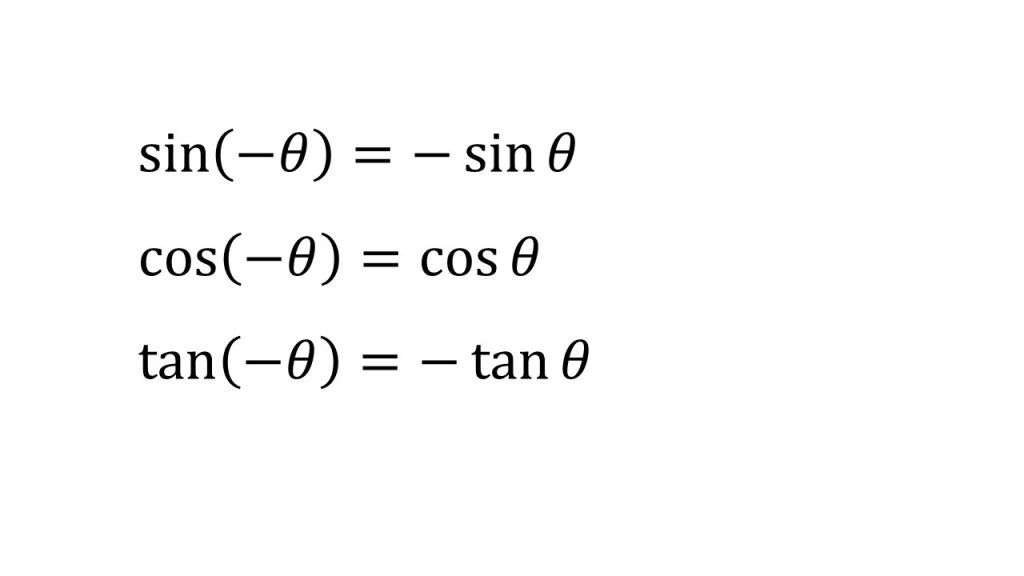
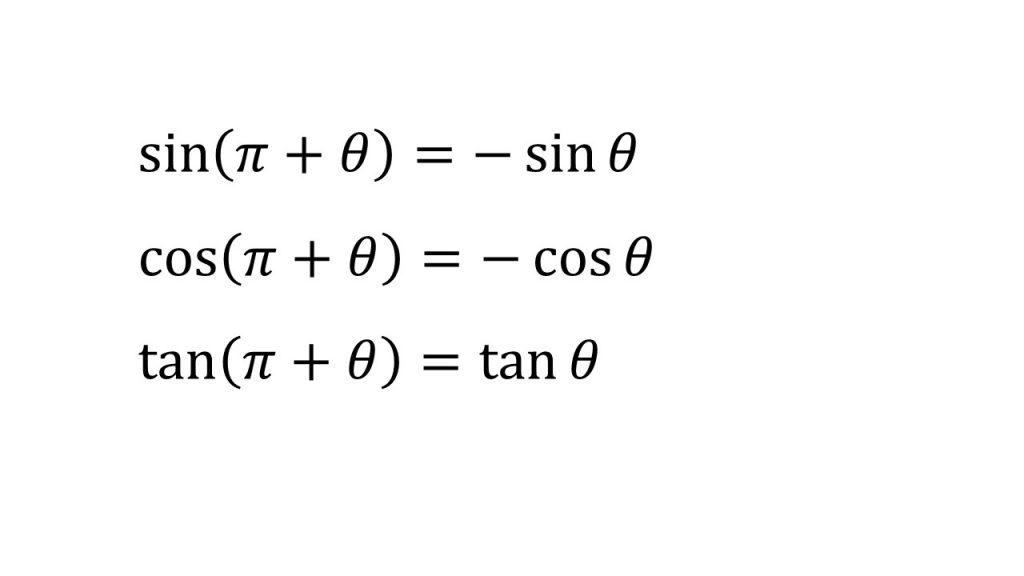
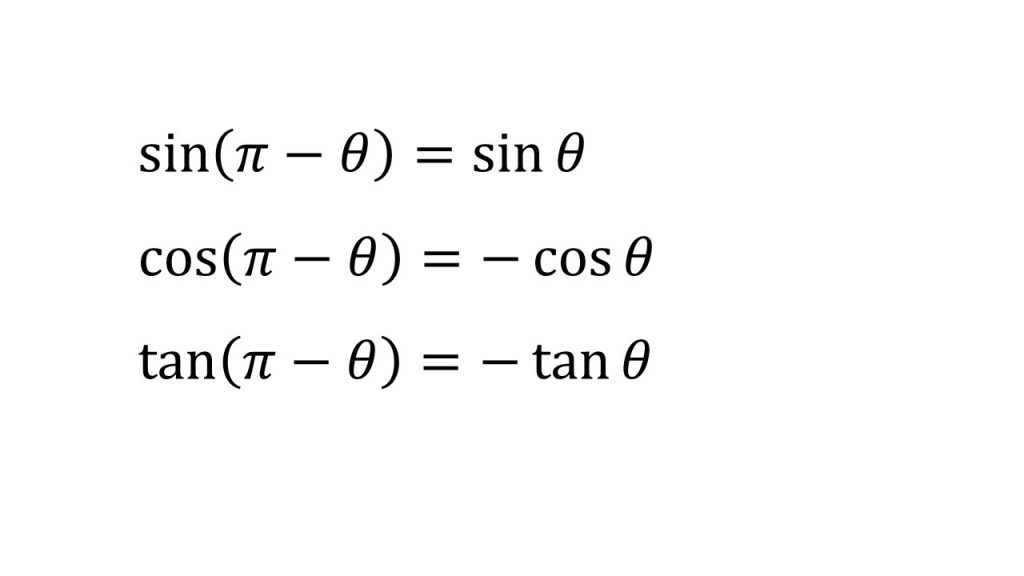
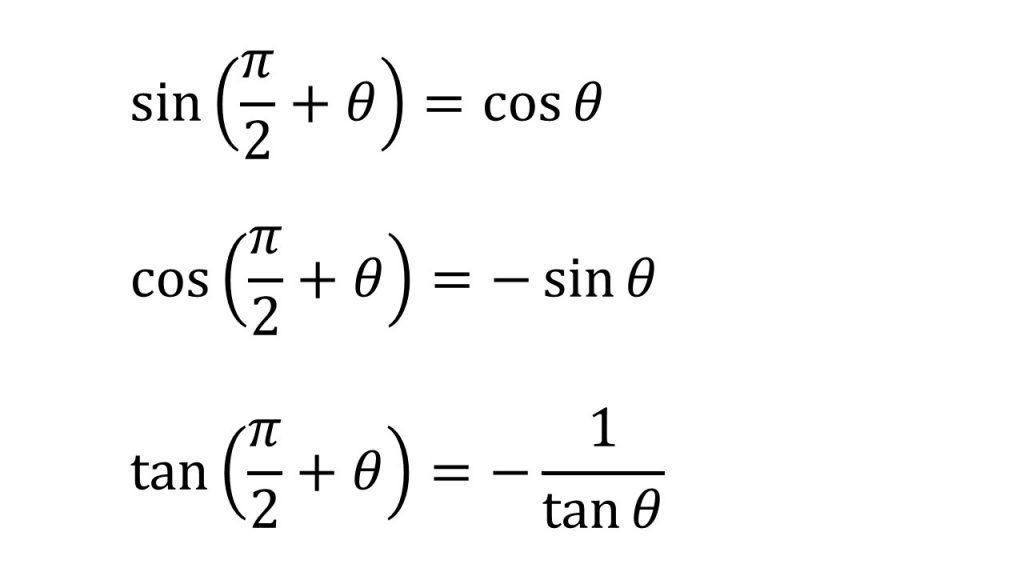
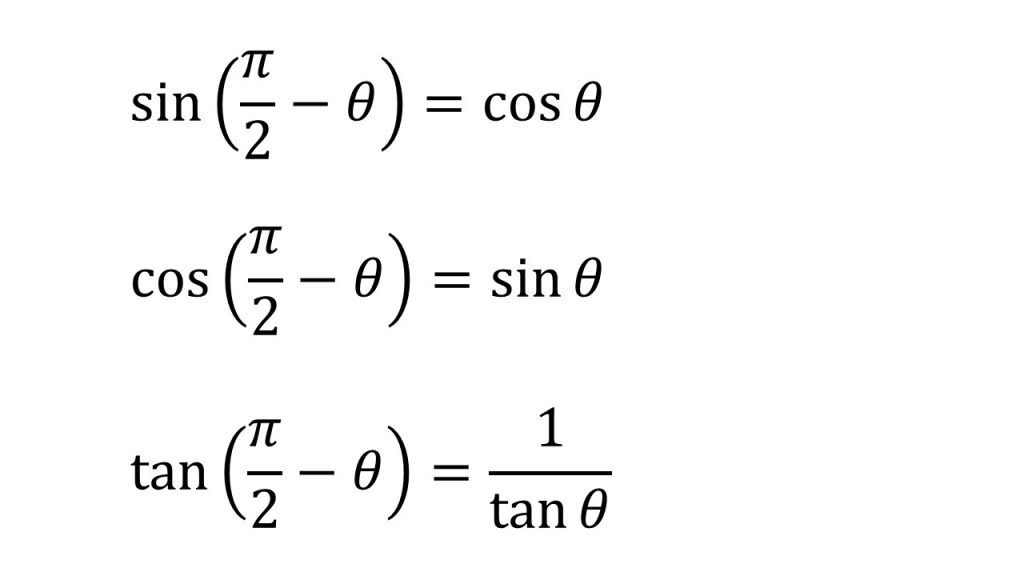
④加法定理
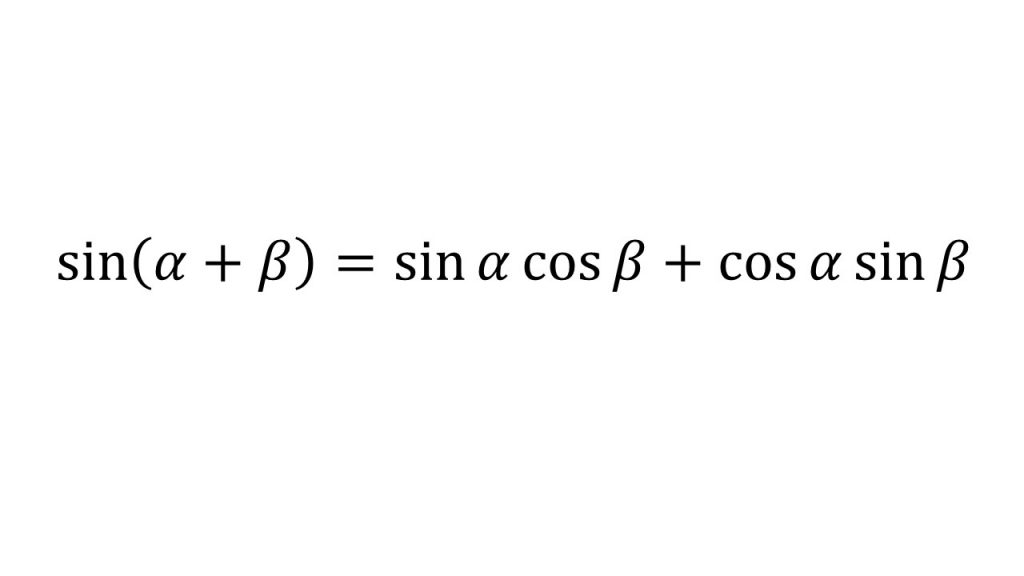
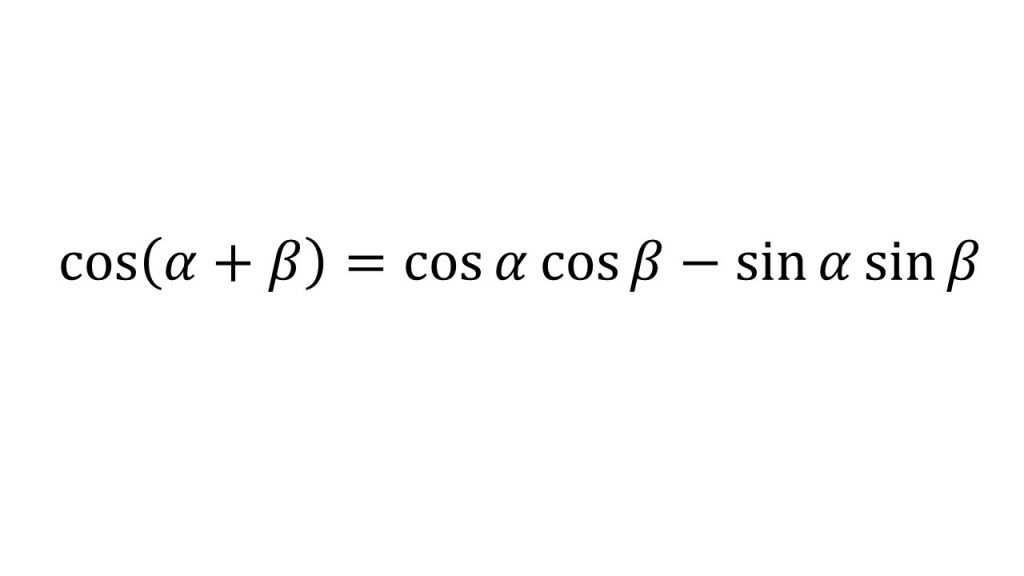
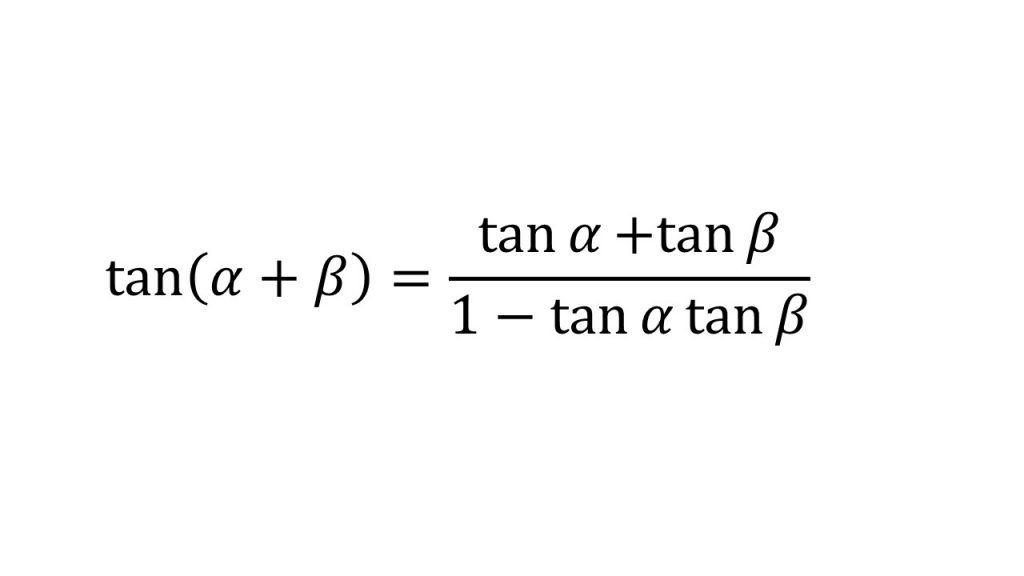
⑤2倍角の公式
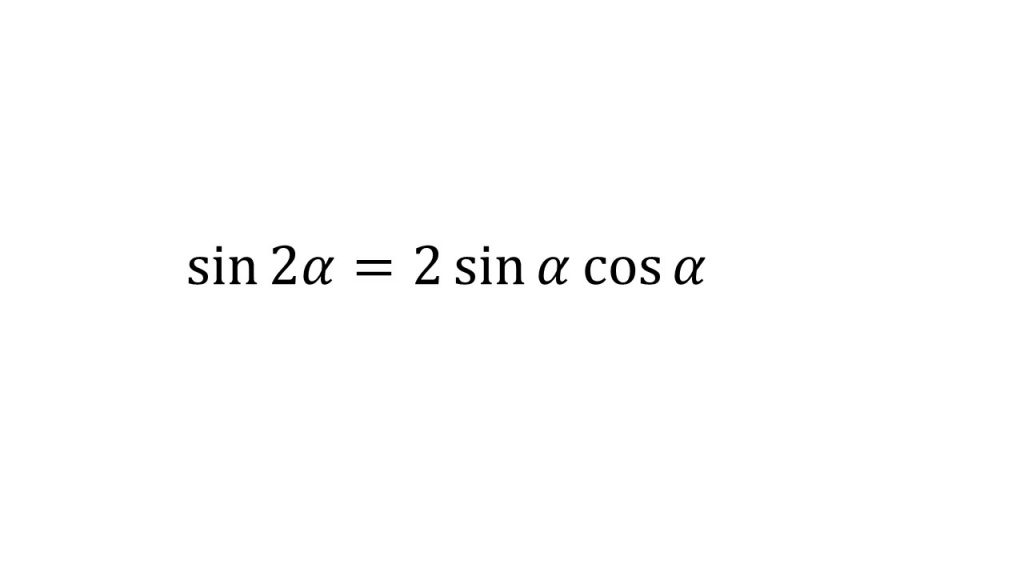
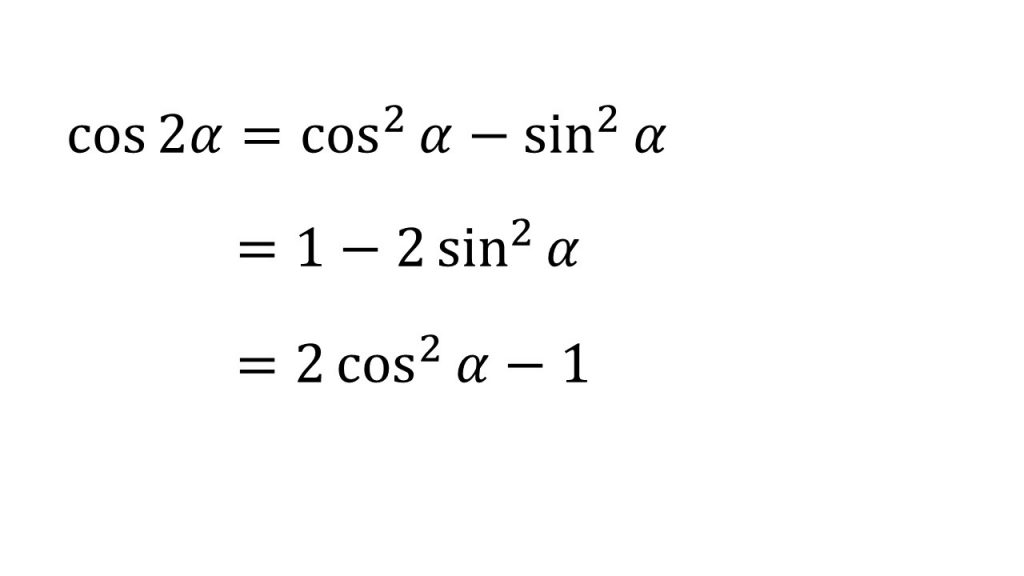
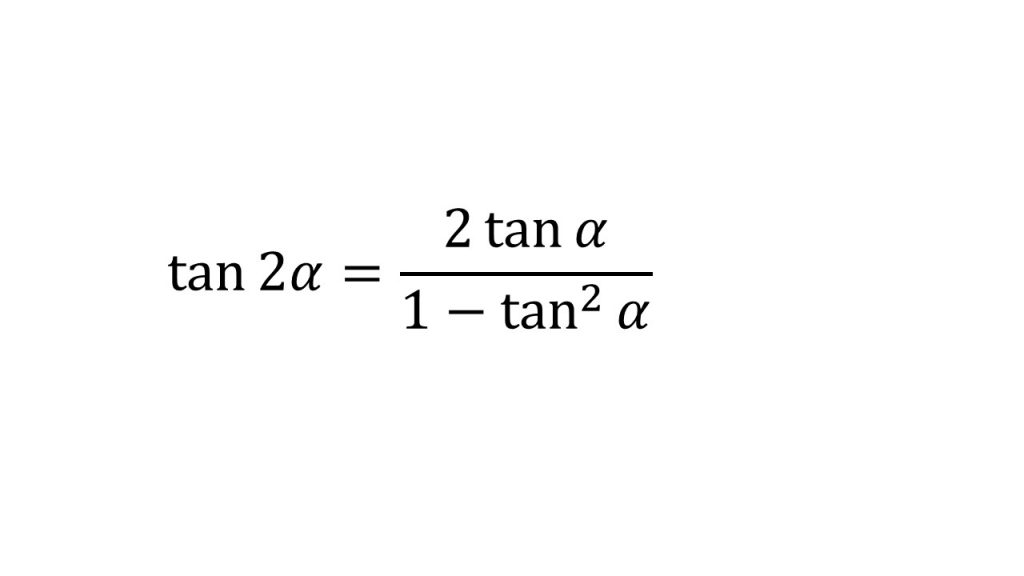
⑥半角の公式
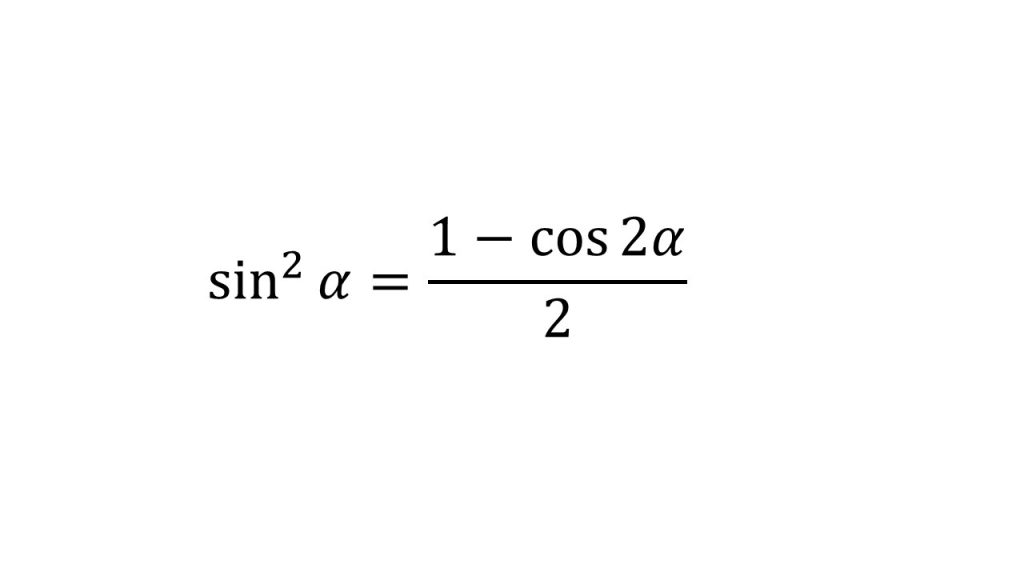
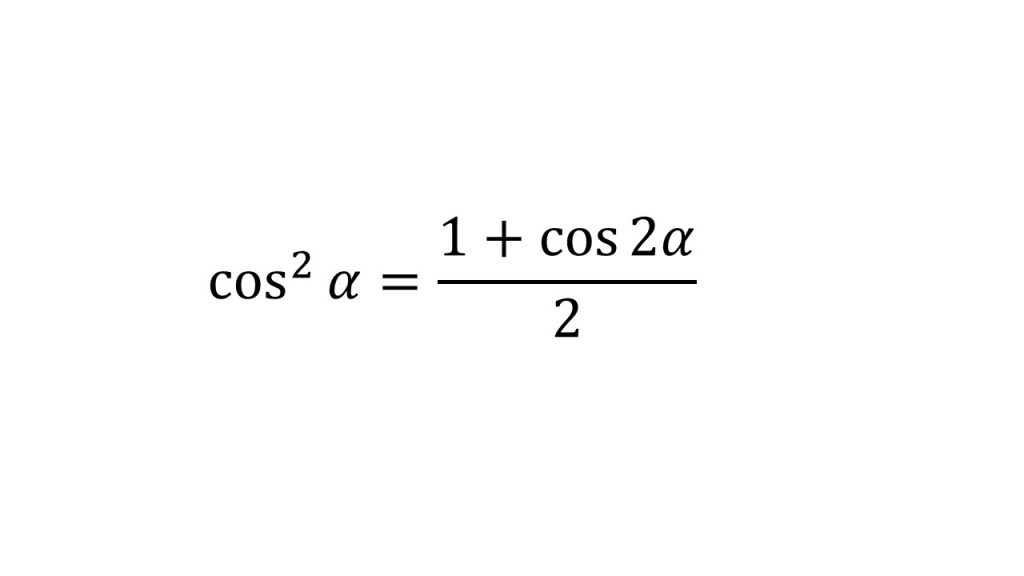
⑦積和の公式
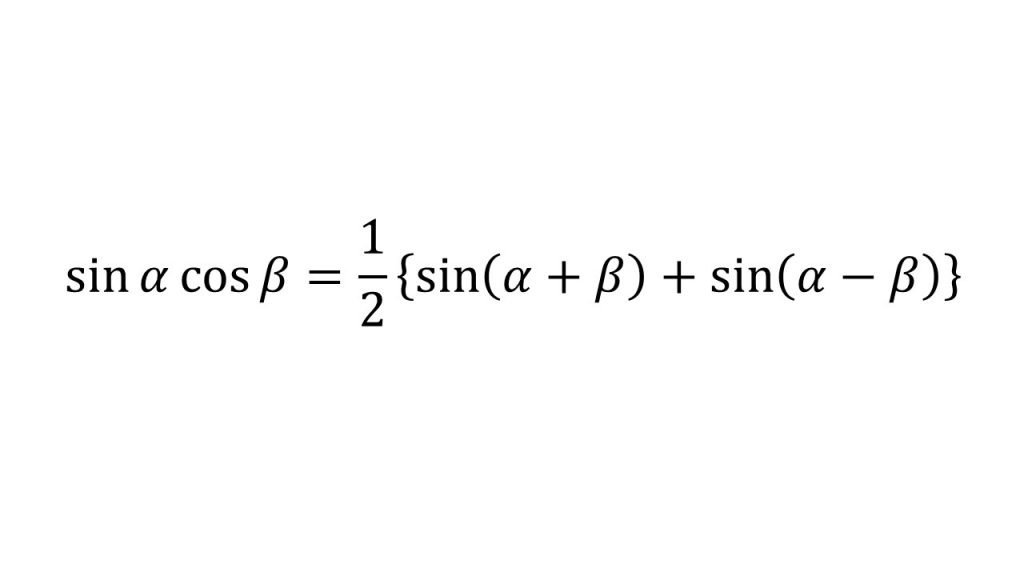
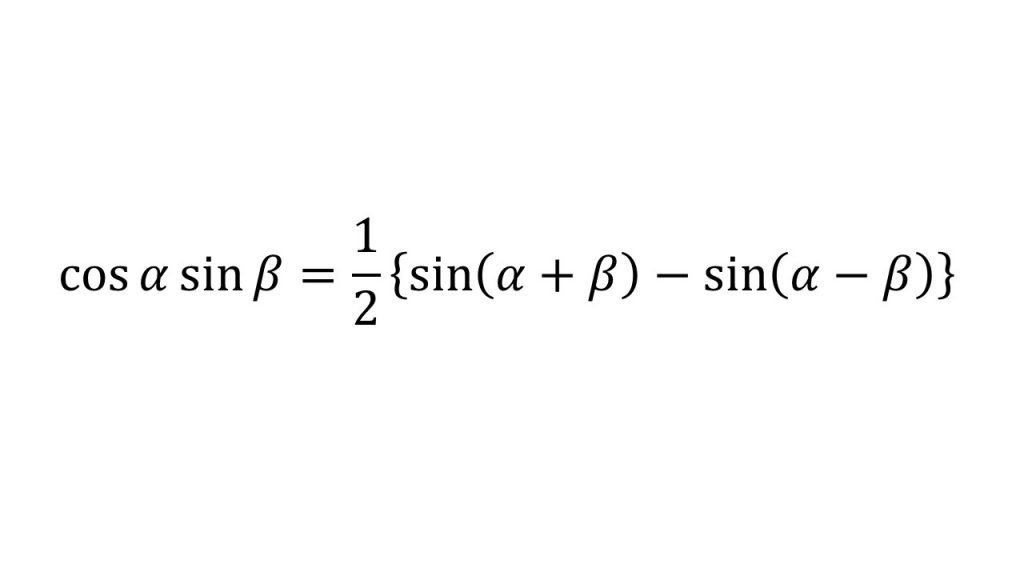
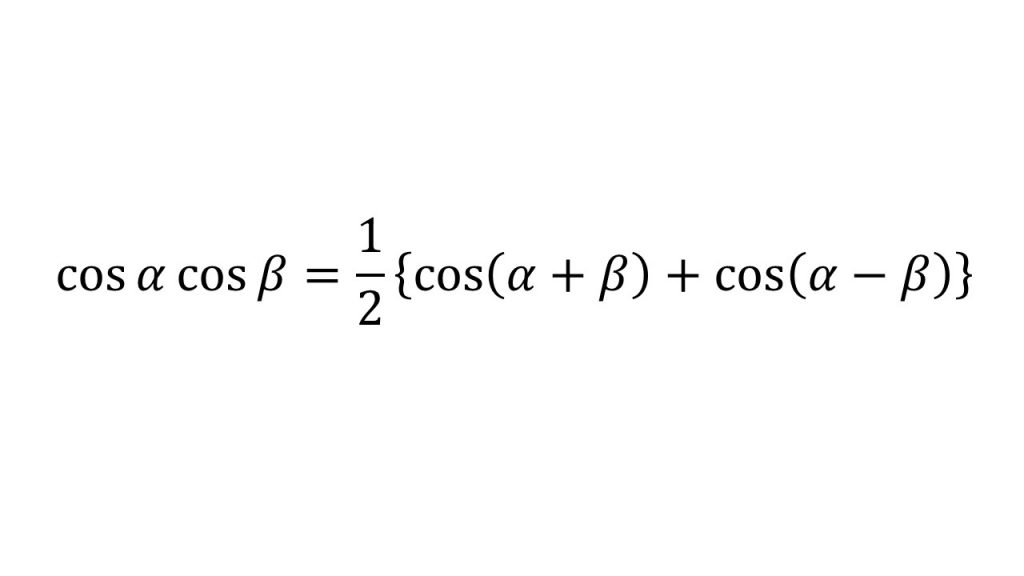
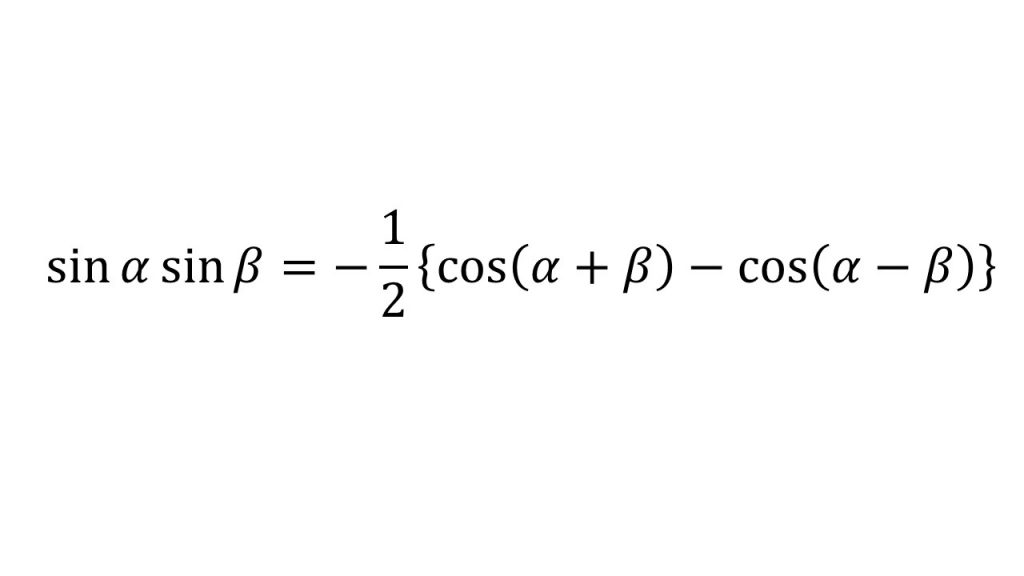
⑧和積の公式
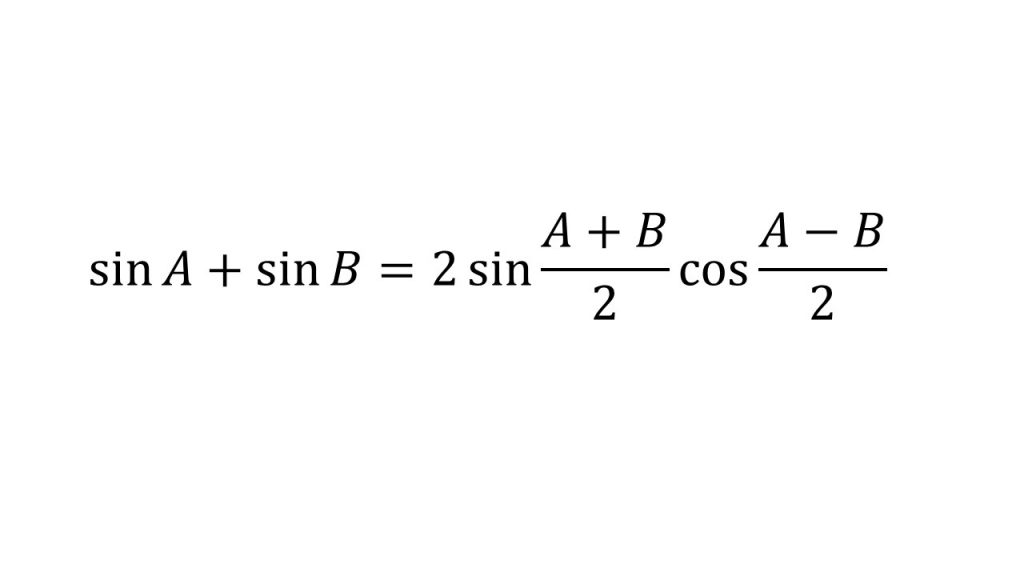
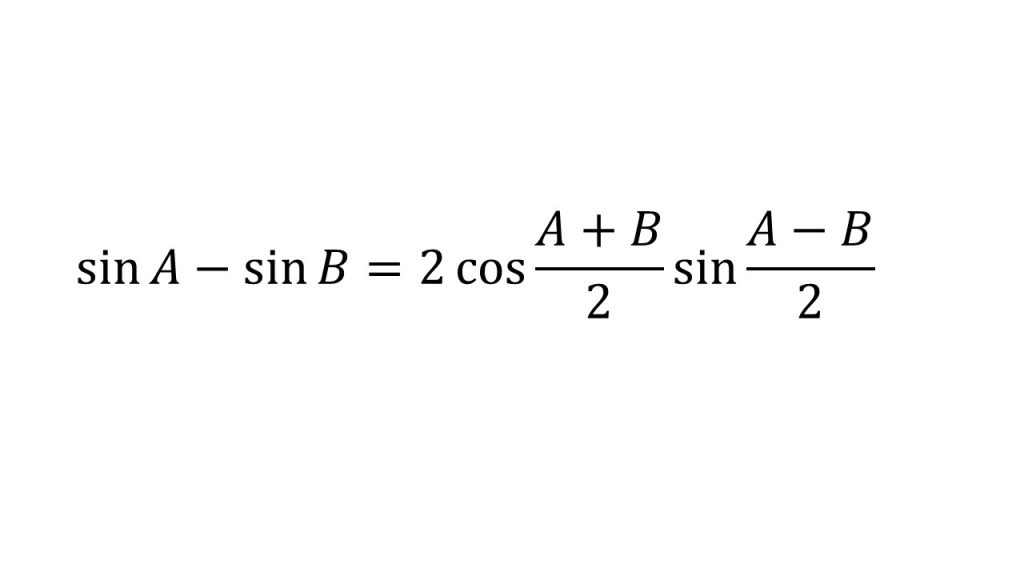
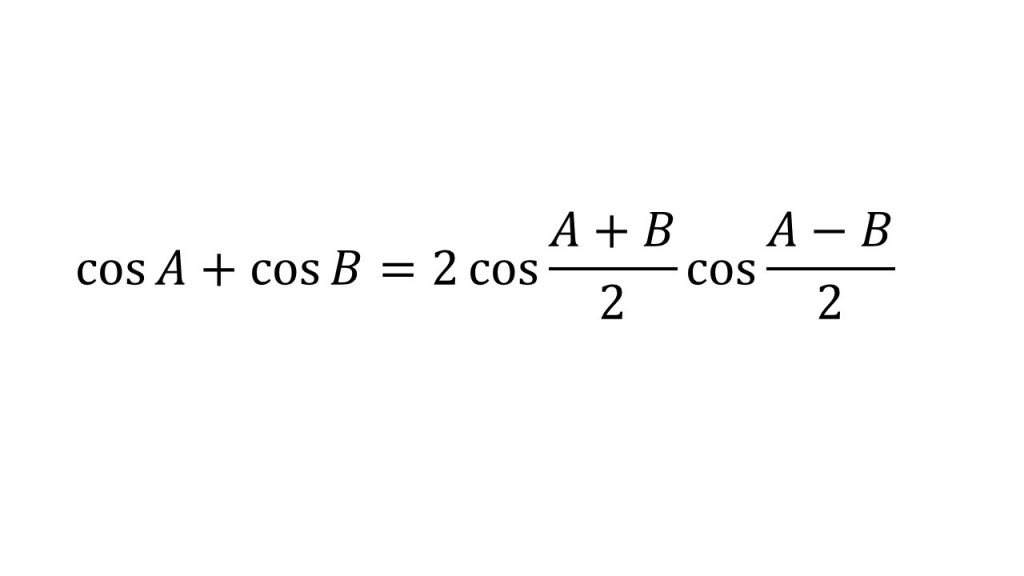
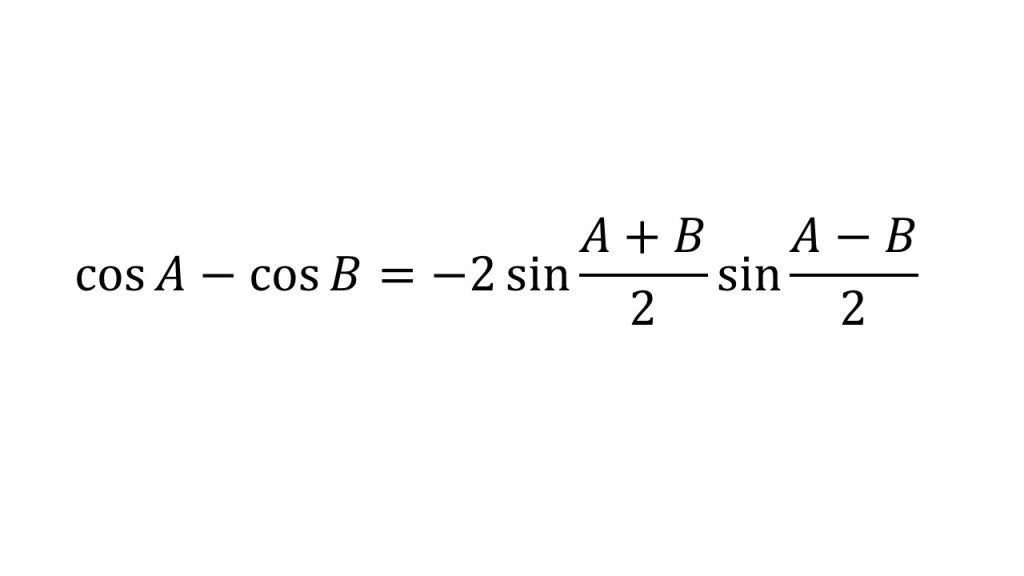
⑨三角関数の合成
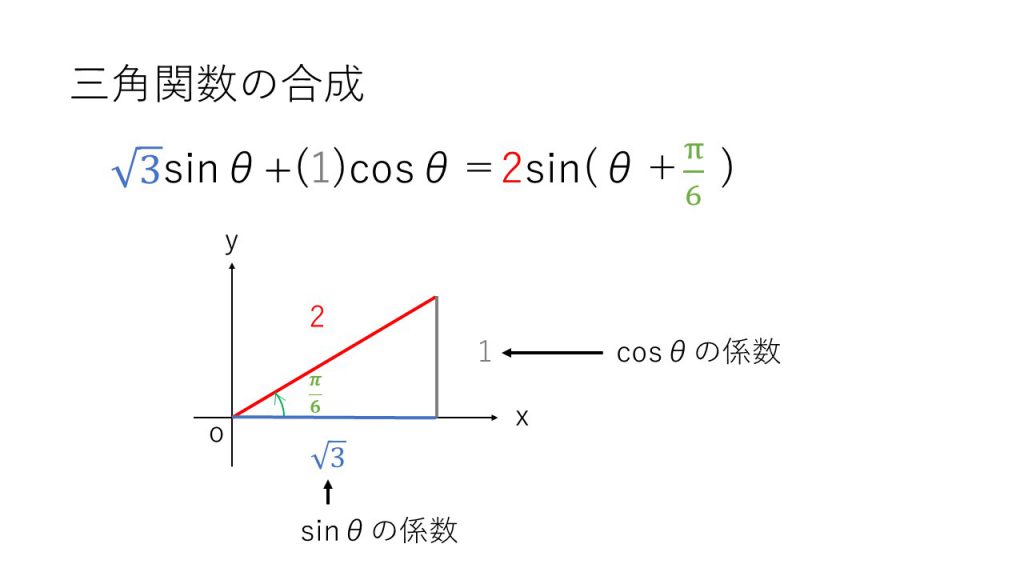
(6)指数
①指数法則
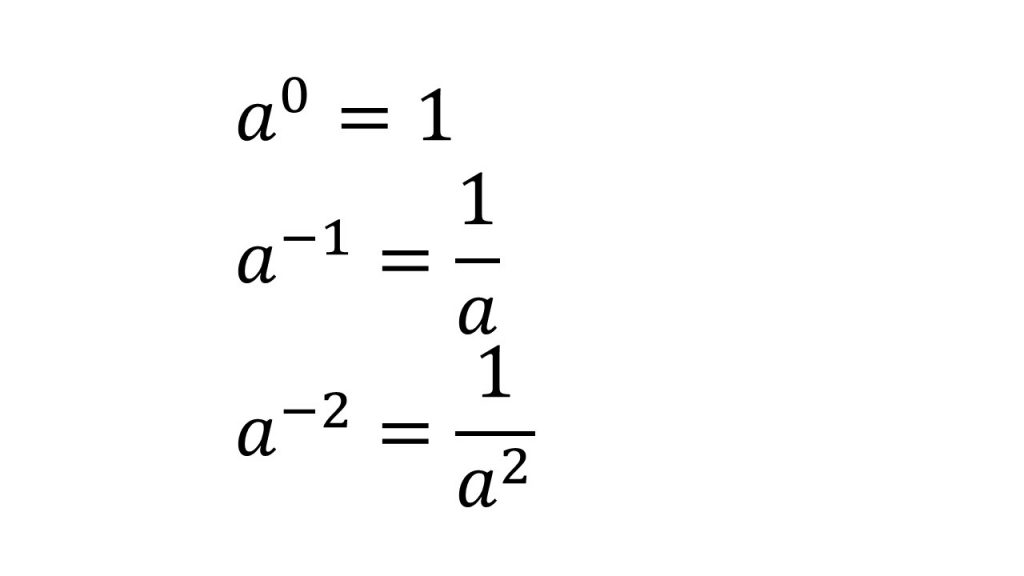
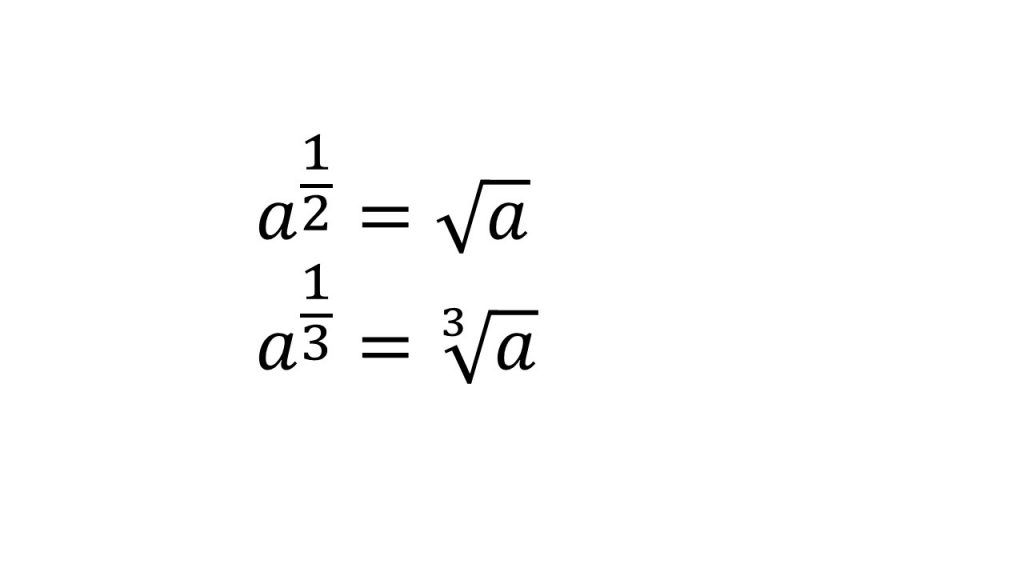
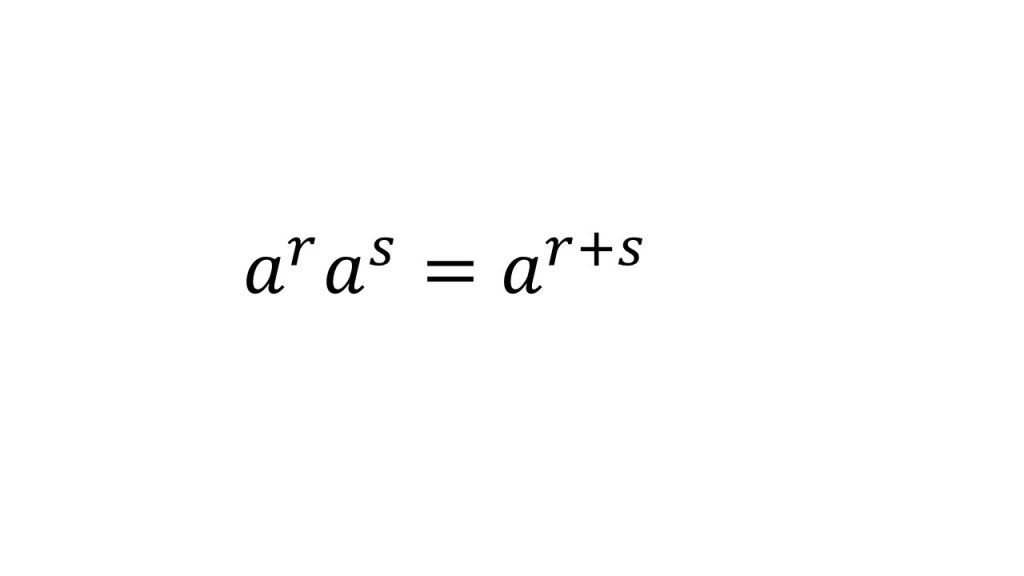
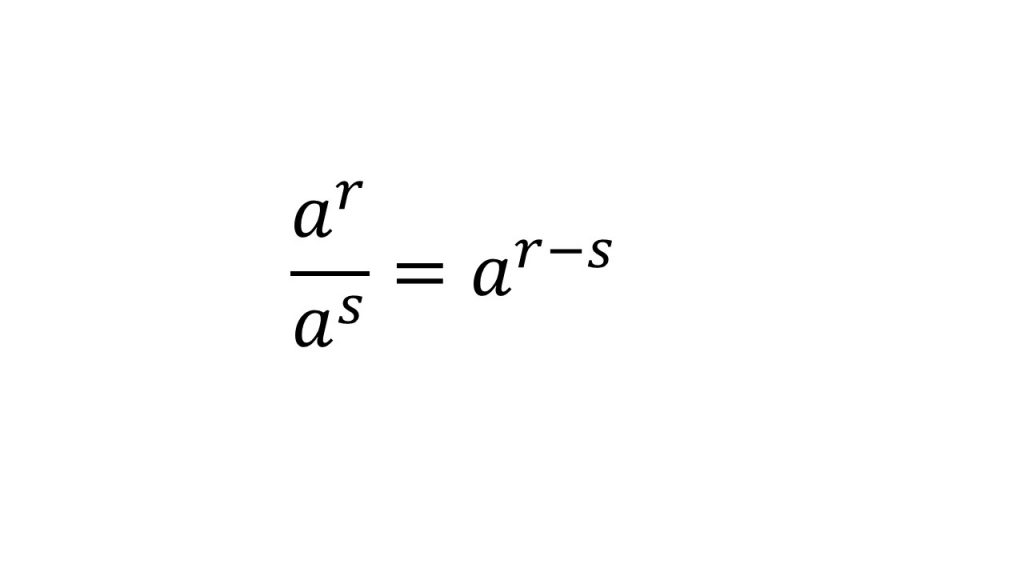
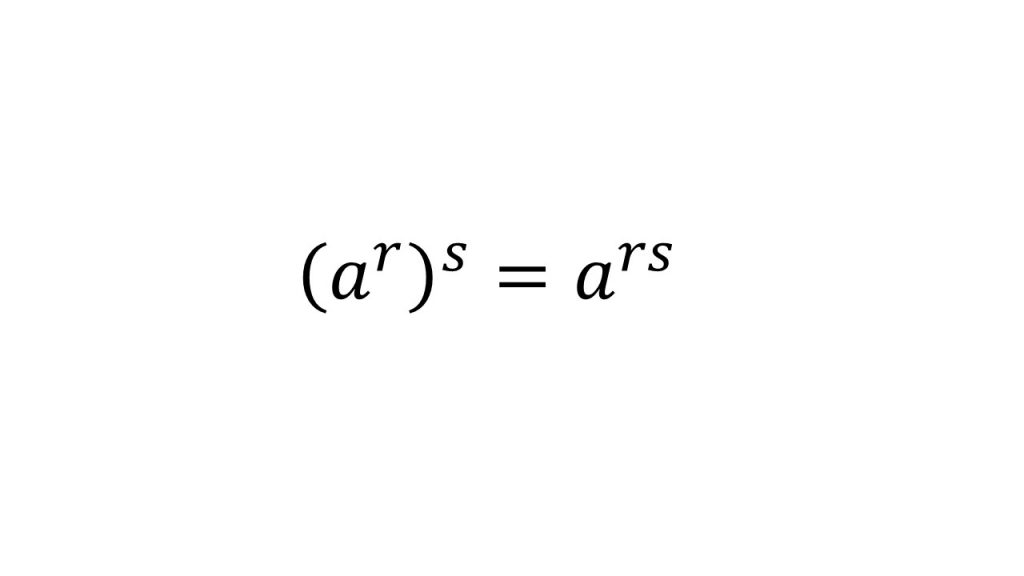
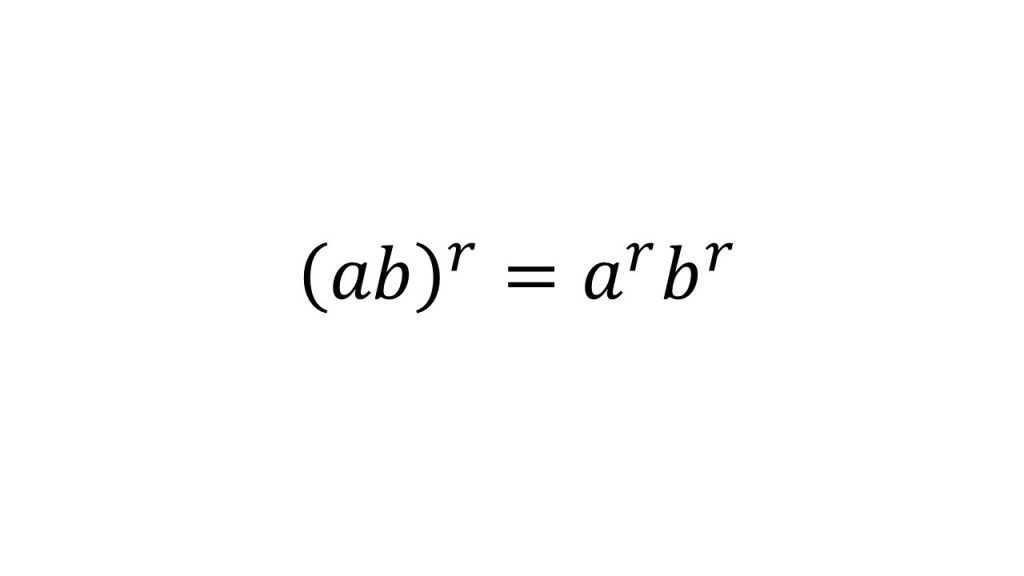
(7)対数
①対数の定義
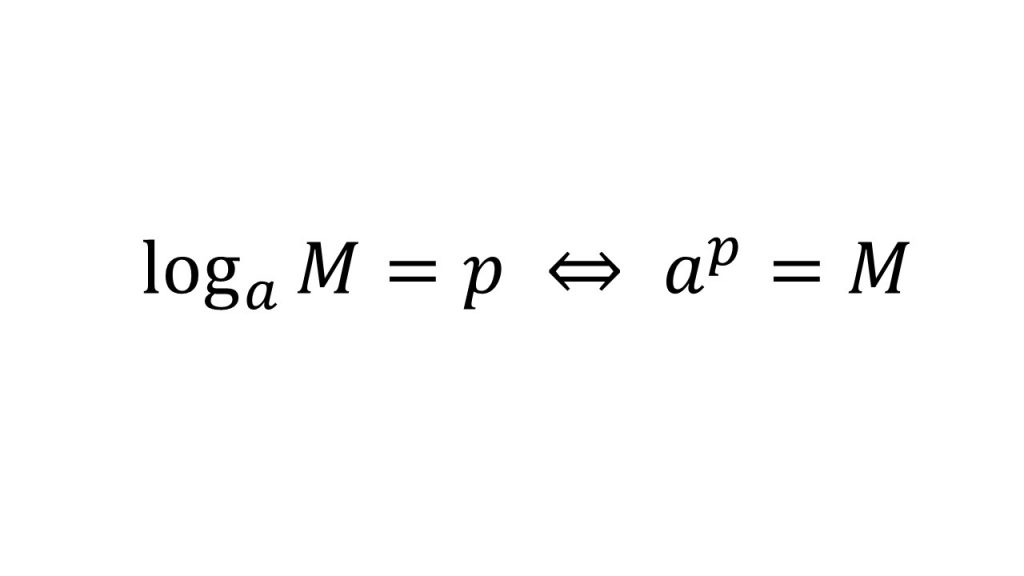
②対数の計算公式4つ
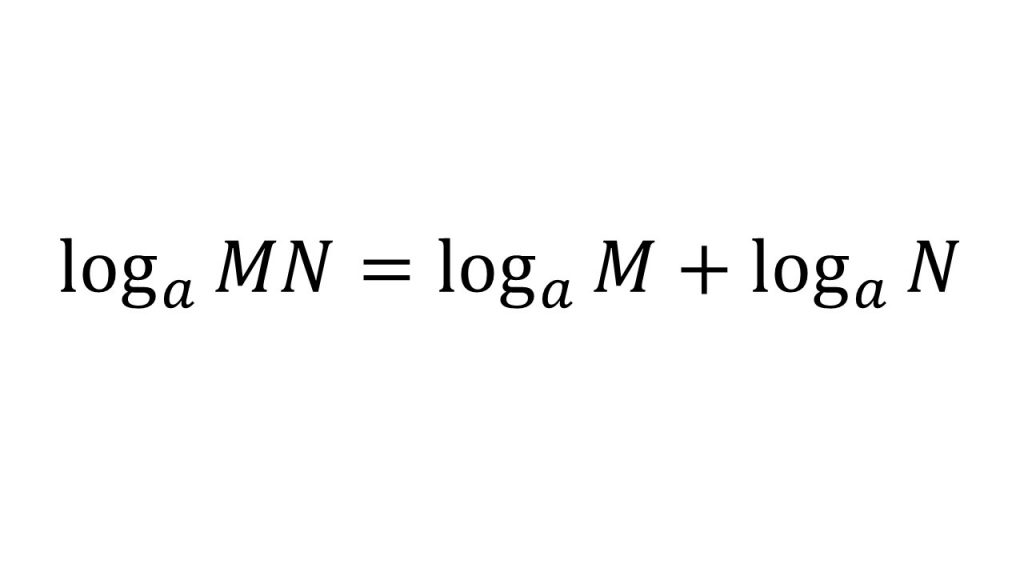
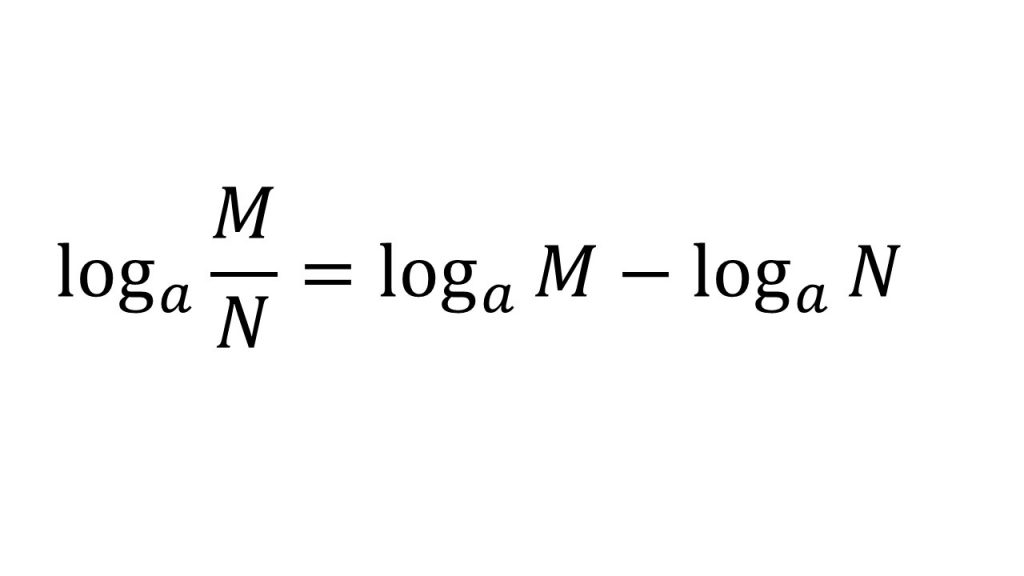
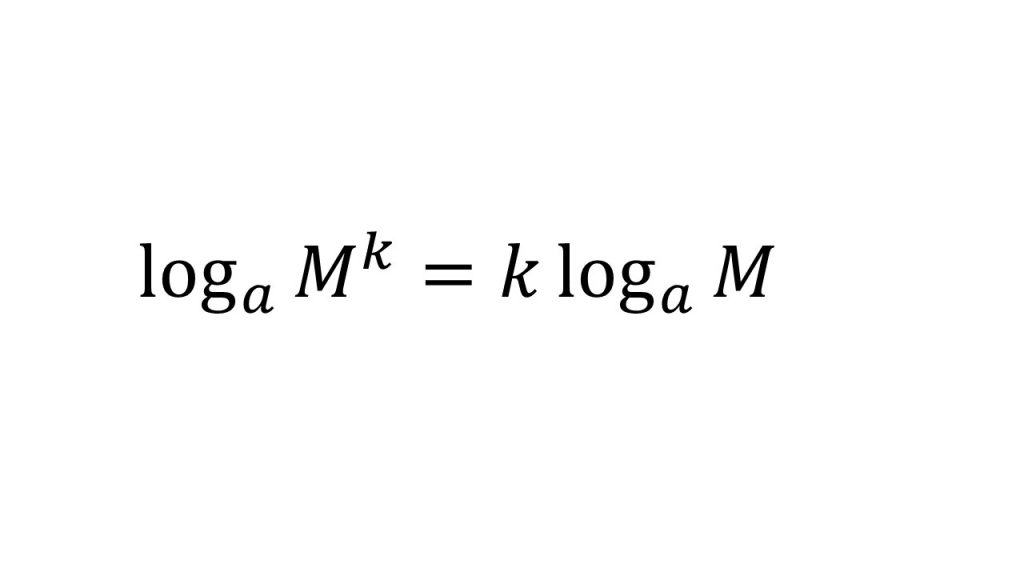
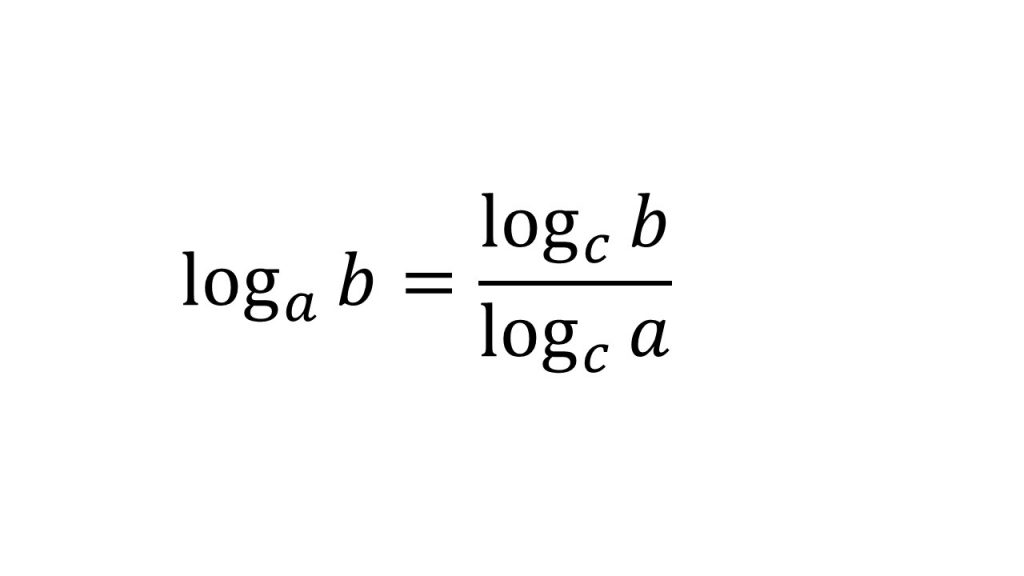
(8)微分
①微分係数の定義

②導関数の定義
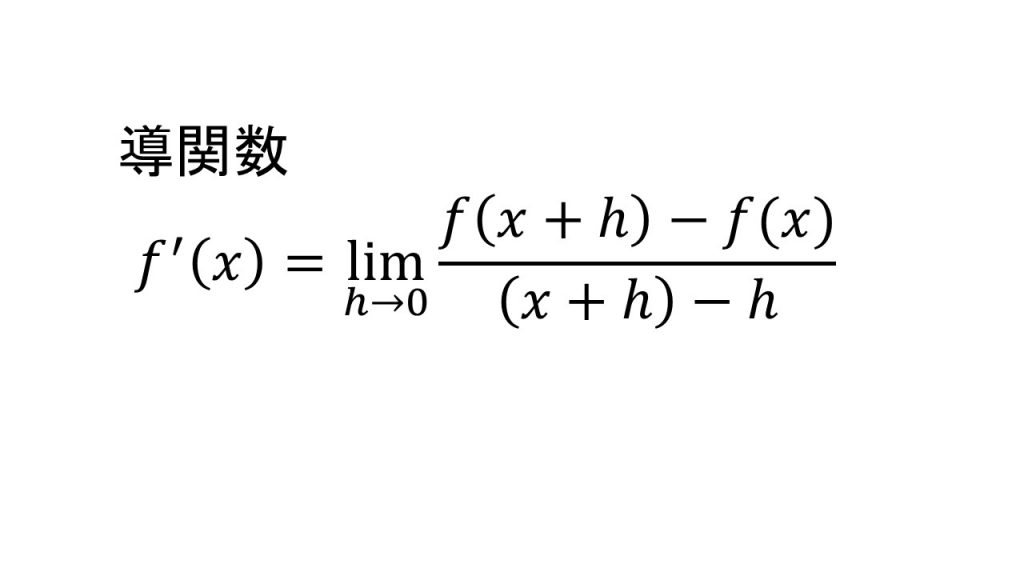
③接線の方程式

④法線の方程式

(9)積分
①積分による面積

②⅙公式