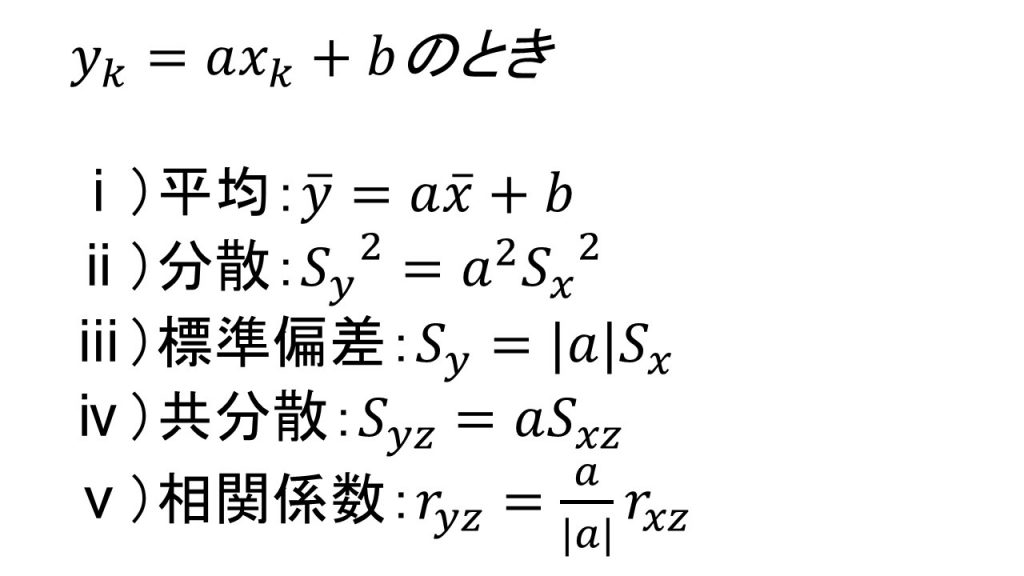(1)展開と因数分解
①知っておきたい展開
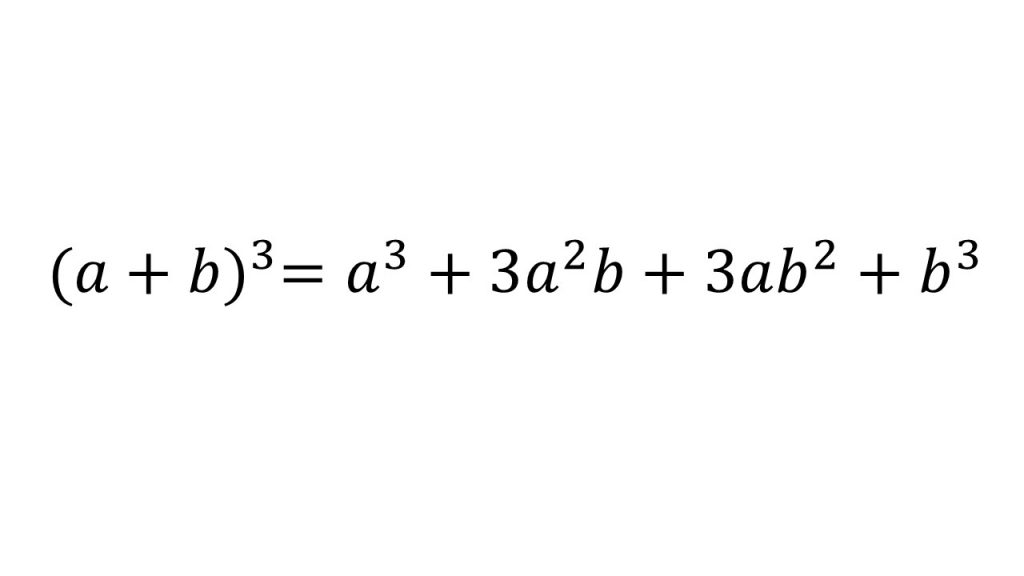
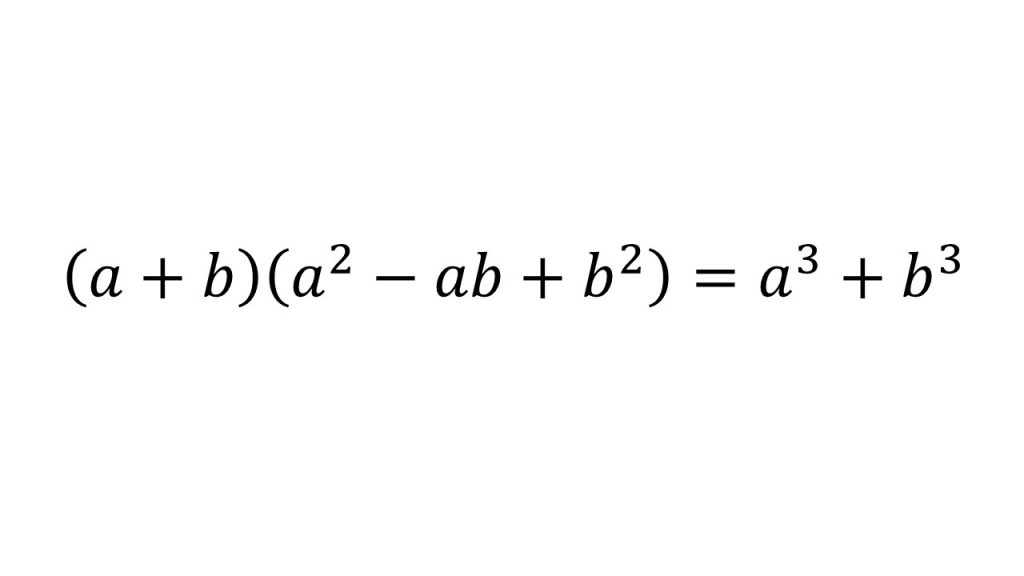
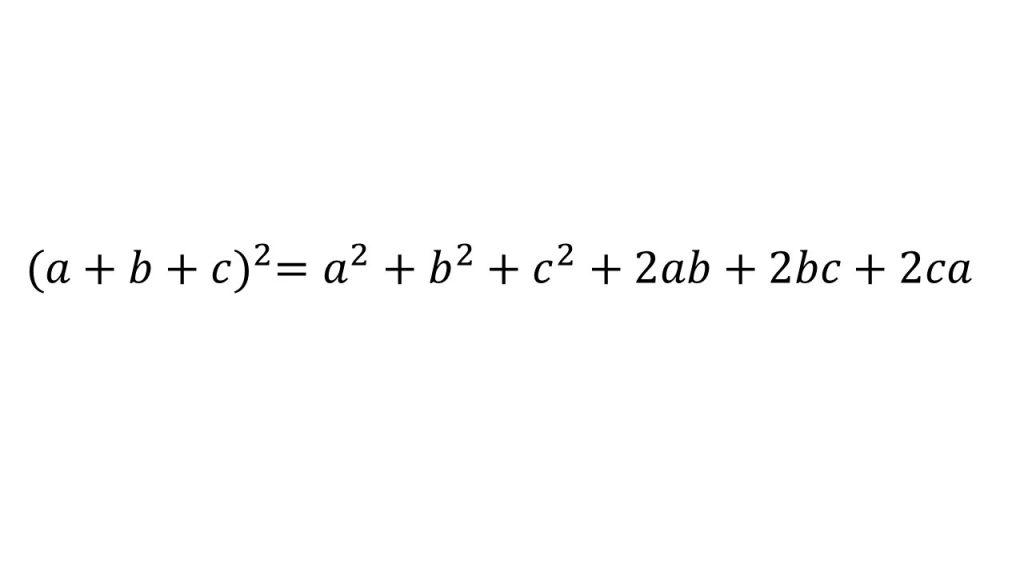
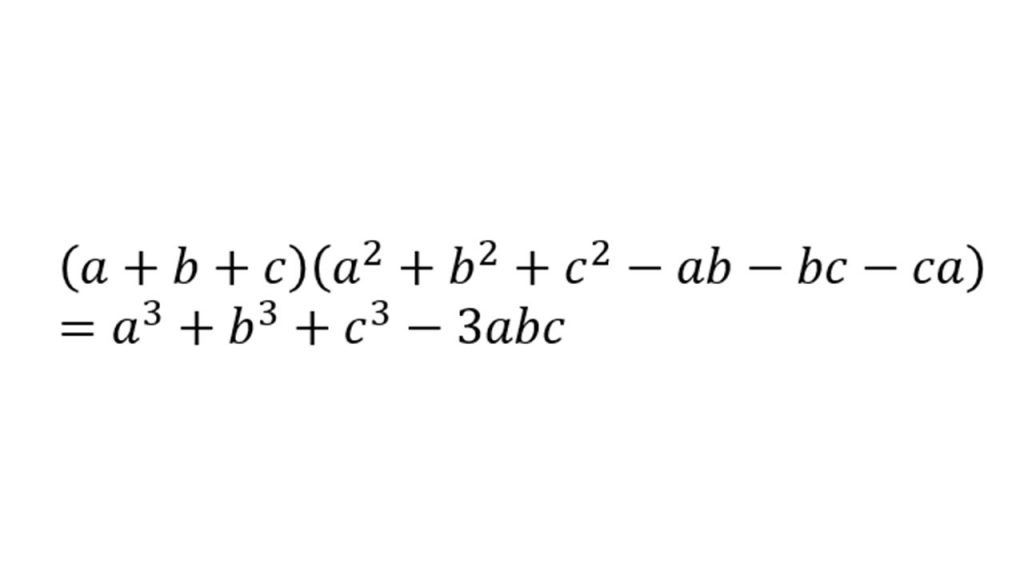
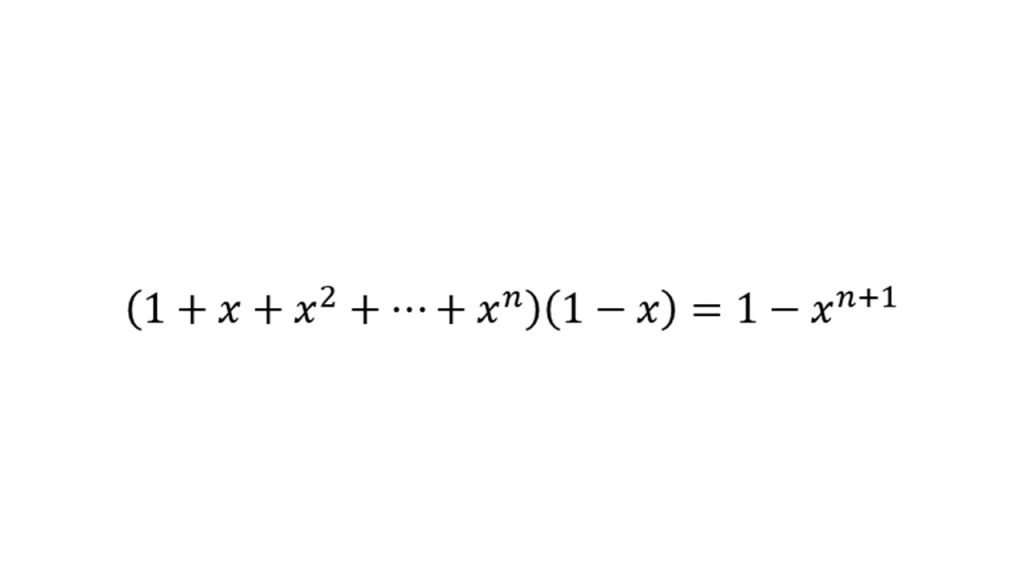
②三次の因数分解
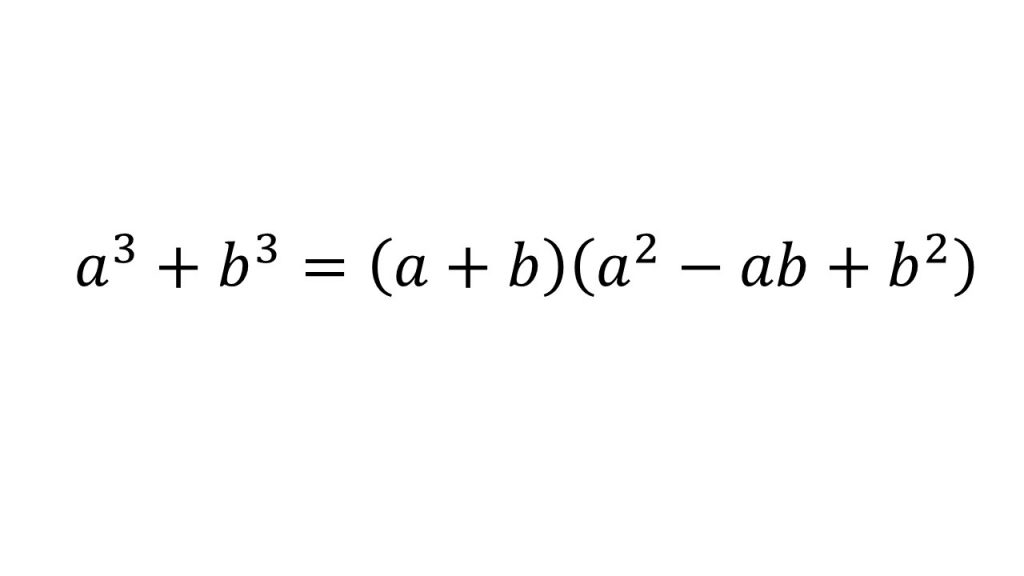
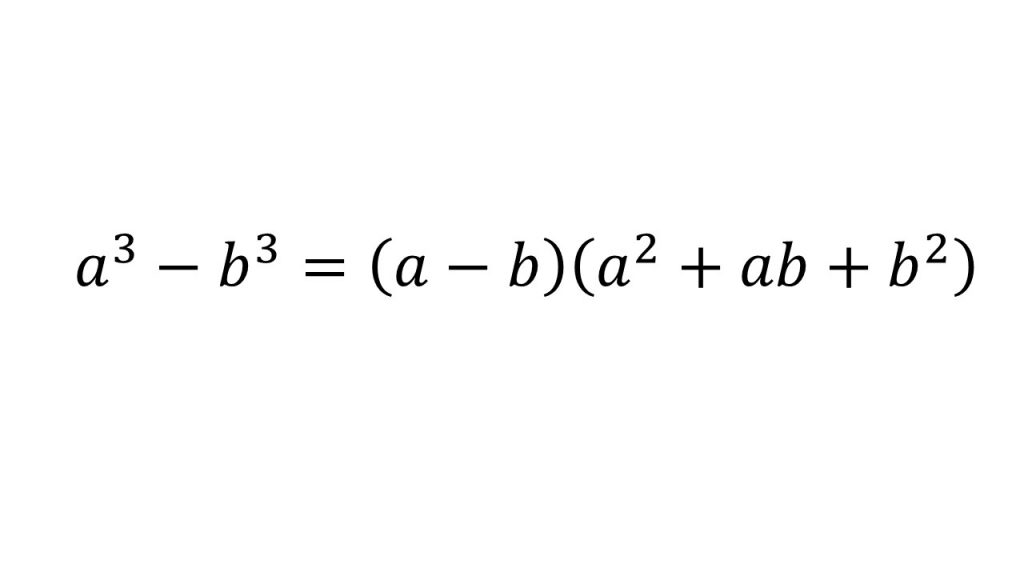
③複二次式の因数分解
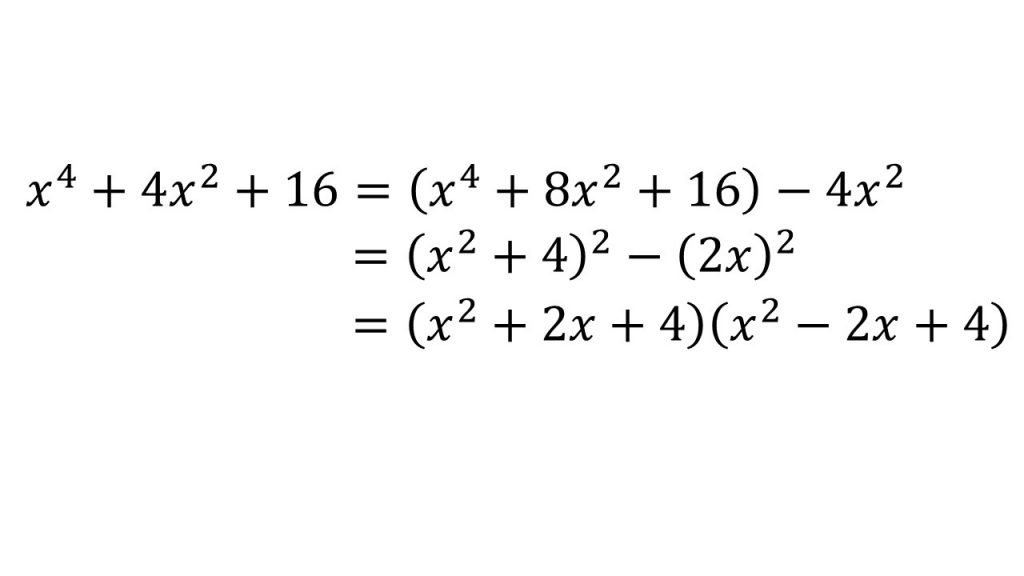
④少し高度な因数分解
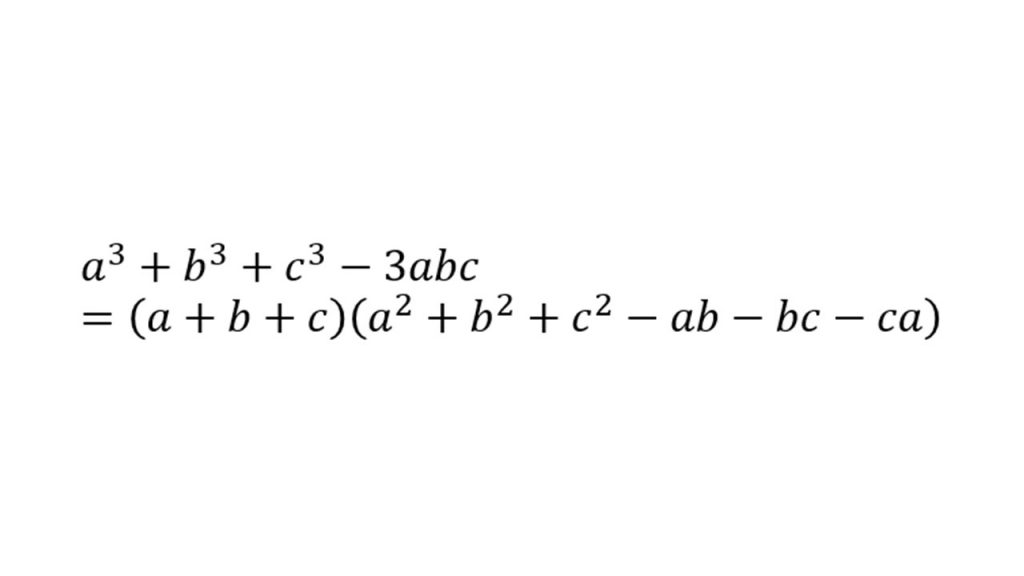
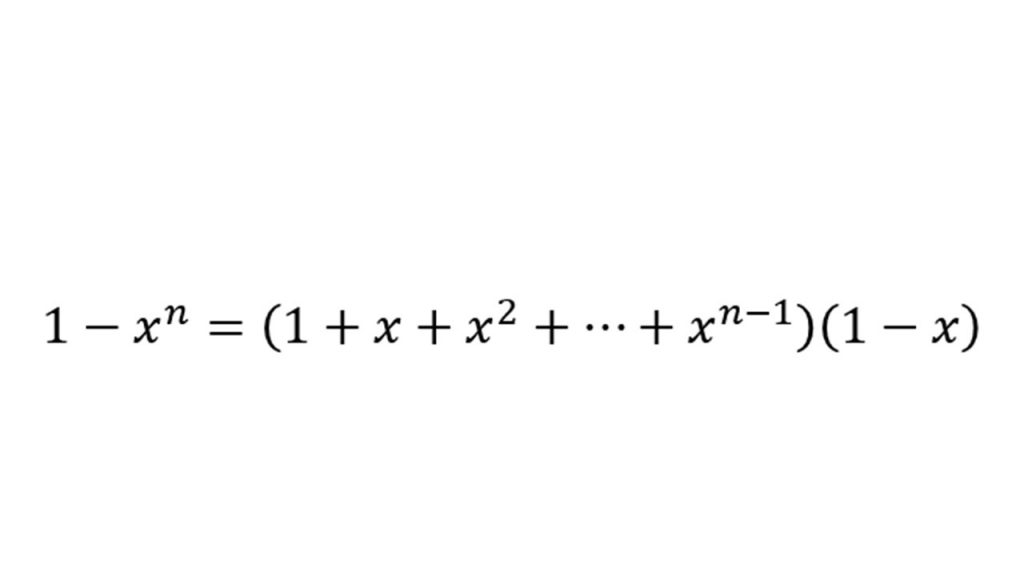
⑤対称式
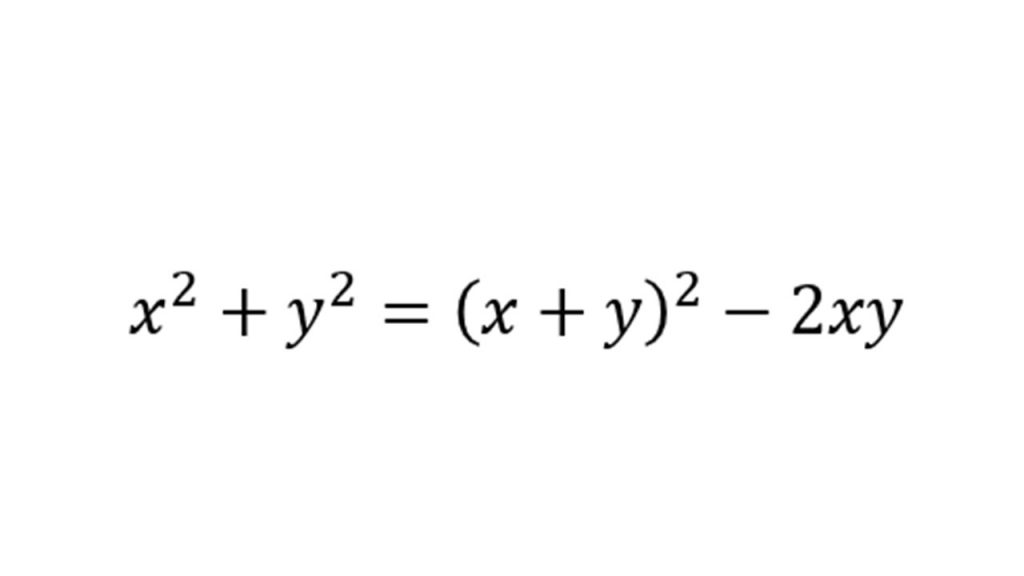
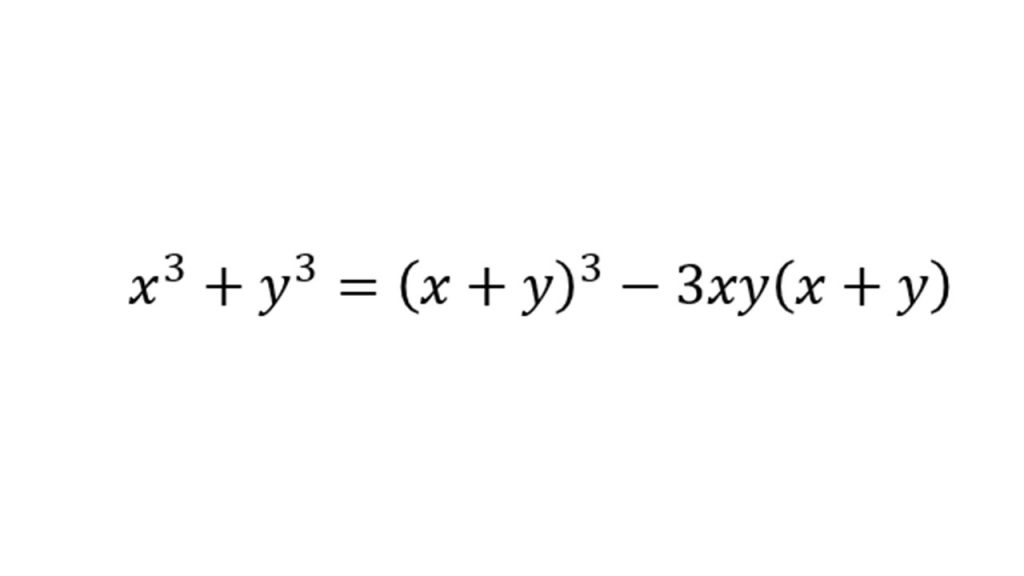
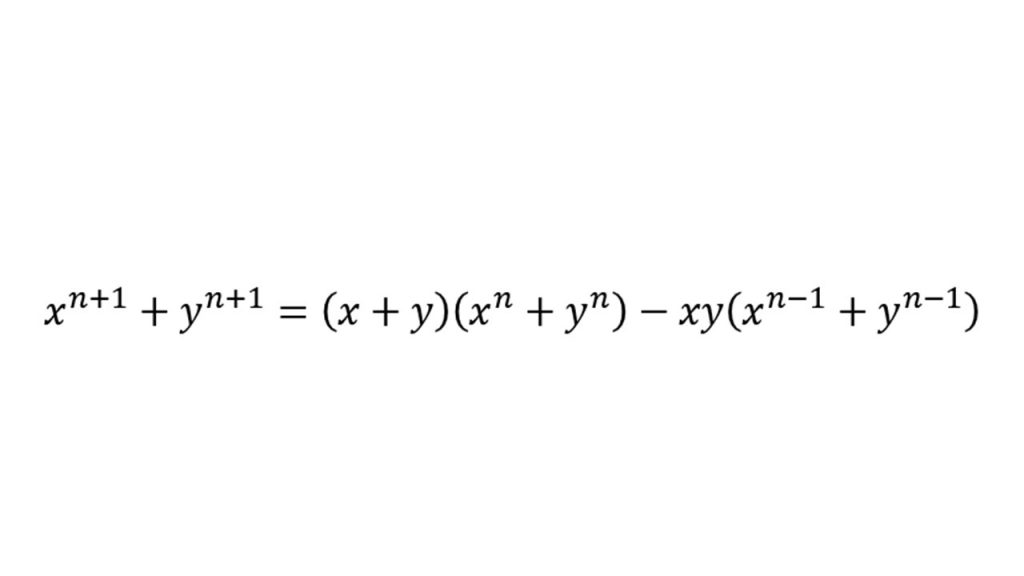
⑥知っておきたい式変形
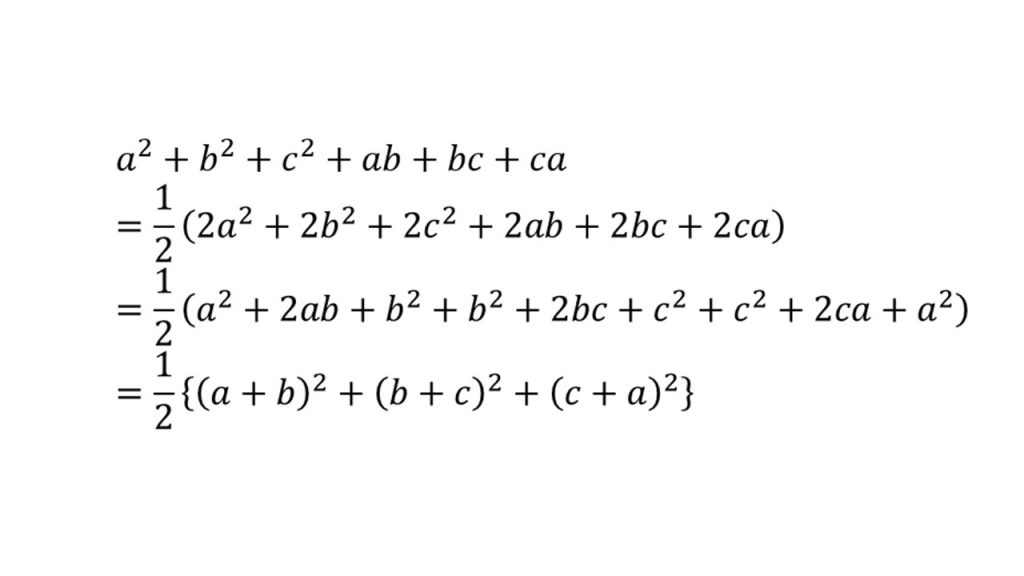
(2)実数
☆数の分類
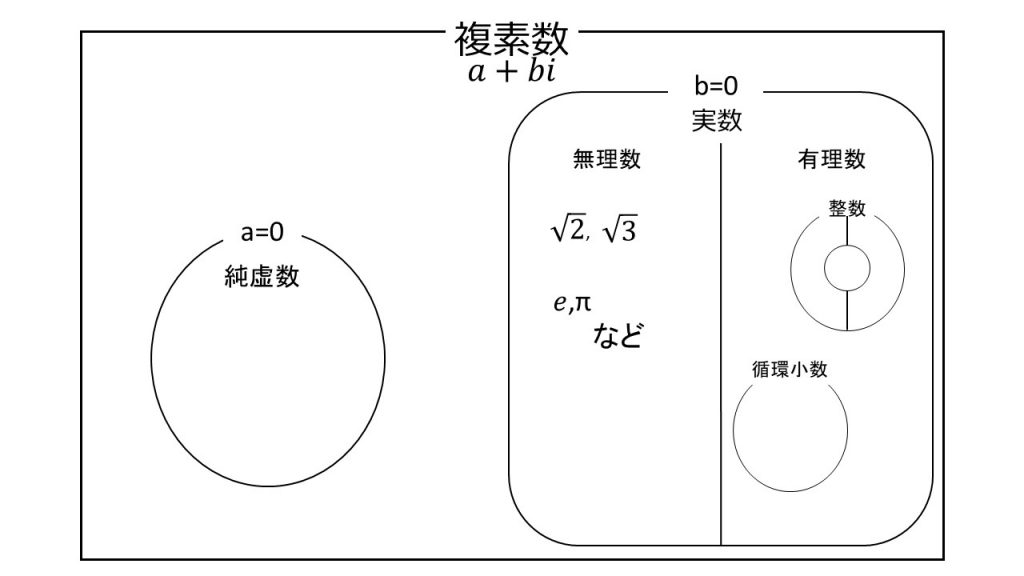
①複素数:a+biと表される数
②純虚数:複素数の実部(a)が0の数
③実数:複素数の中で虚部(b))が0の数
④有理数:整数p, qを使ってq/pと表すことができる数
※循環小数は有理数
※有理数どうしで四則演算(+、-、×、÷)をしても有理数である。
⑤無理数:有理数ではない実数
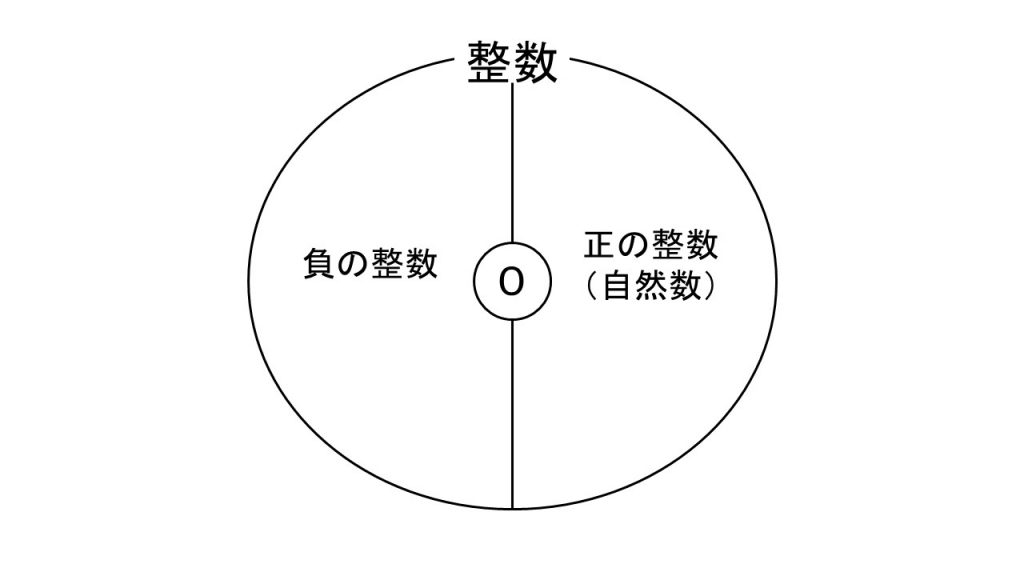
⑥整数は、負の整数・0・正の整数(自然数)に分けられる。
※0は自然数ではない。
⑦自然数は、1・素数・合成数に分けられる。
※1は素数ではない。
⑧素数:約数が2つの自然数
※2は唯一の偶数の素数(2以外の素数は全て奇数)
⑨合成数:素数の積でできている自然数
(3)1次不等式
①絶対値の等式

※xが絶対値の中にあるときのみ使える。絶対値の外にxが含まれているときは場合分けをする。
②絶対値の不等式

※xが絶対値の中にあるときのみ使える。絶対値の外にxが含まれているときは場合分けをする。
(4)集合
①a∊A:aは集合Aの要素

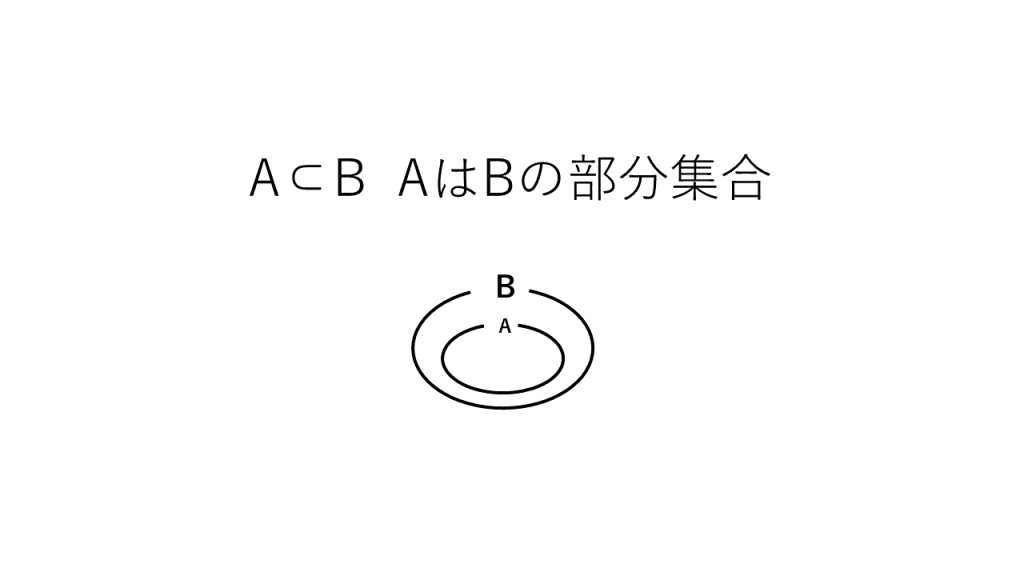
②A⊂B:AはBの部分集合
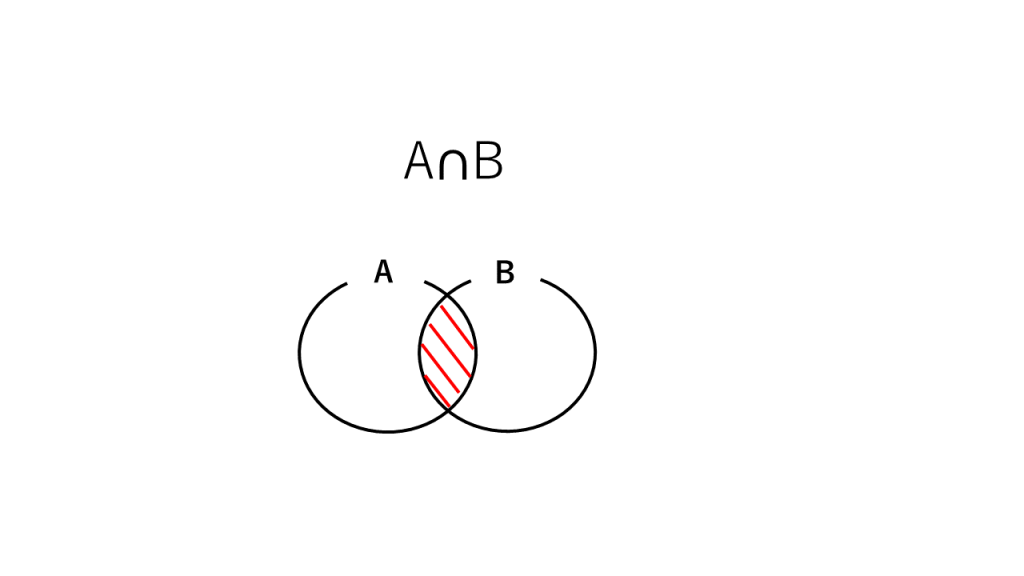
③A∩B:AかつB、AとBの共通部分
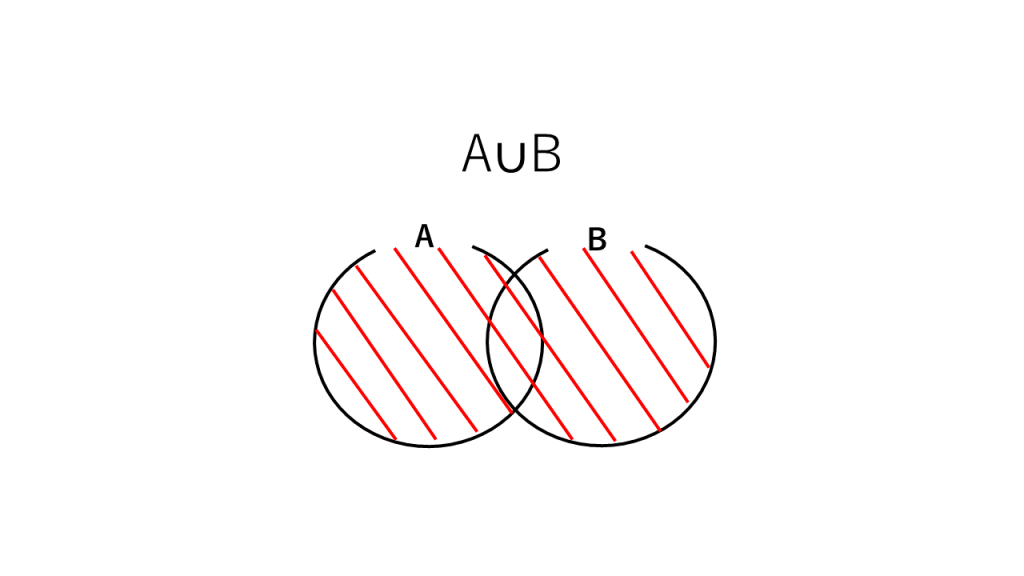
④A∪B:AまたはB、AとBの和集合
⑤Aの否定、Aではない
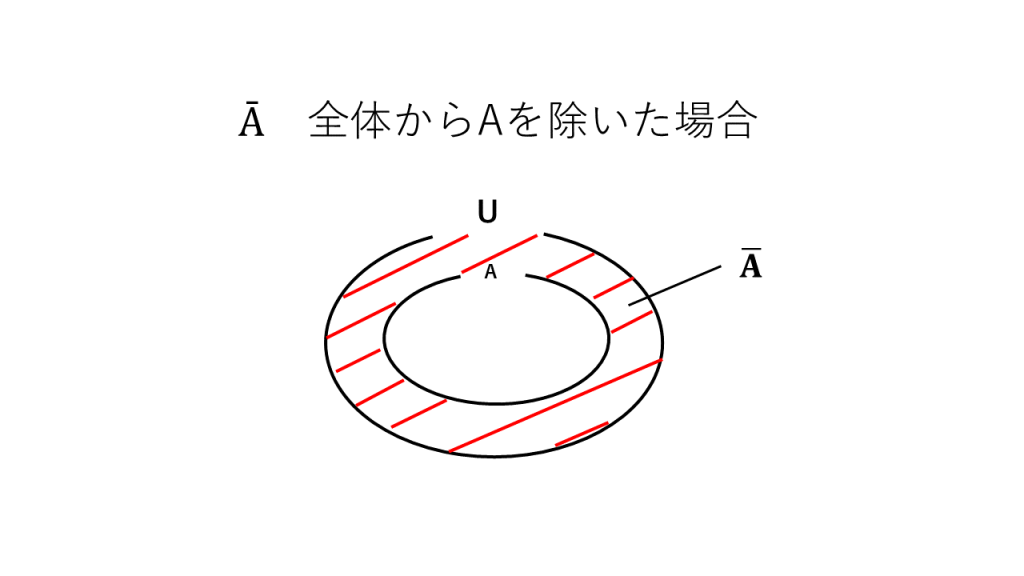
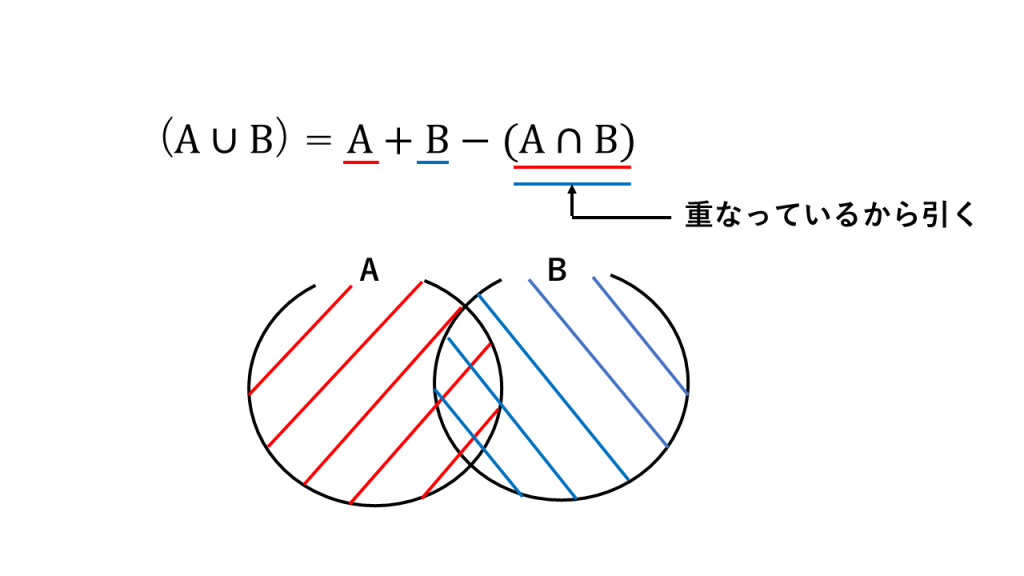
⑥和集合の求め方
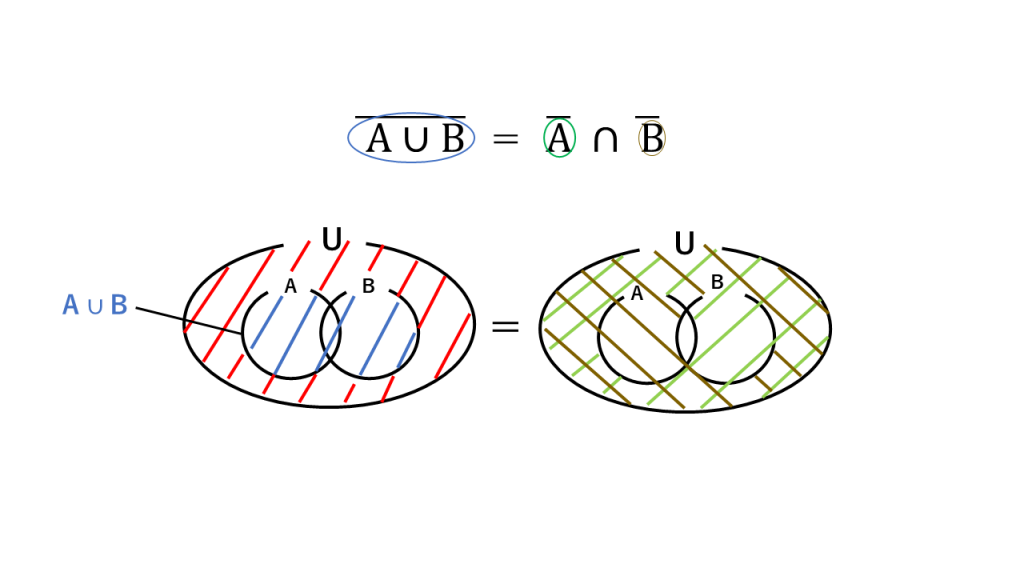
⑦ド・モルガンの法則
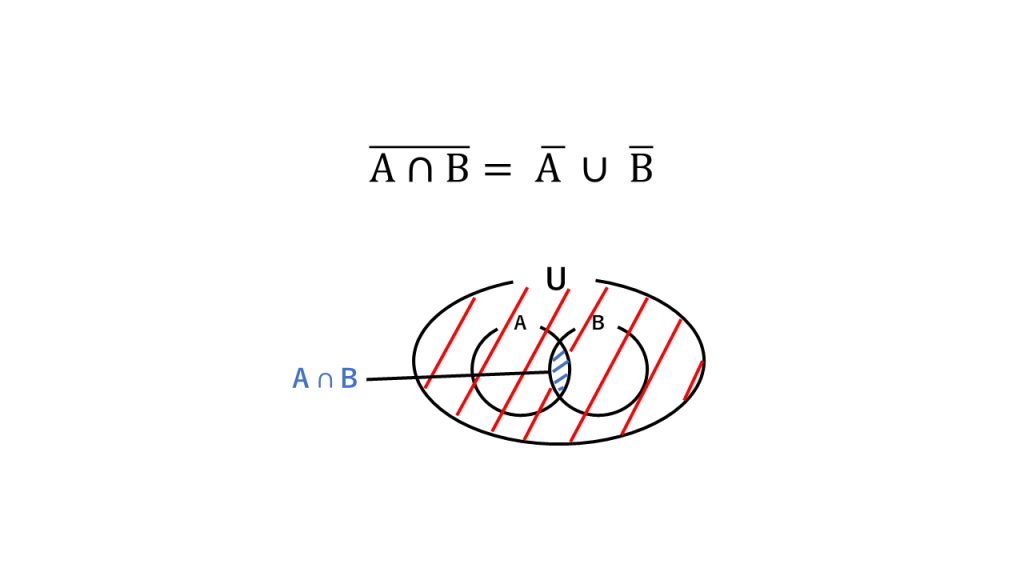
⑧3つの和集合
(A∪B∪C)=A+B+C−(A∩B)−(B∩C)−(C∩A)+(A∩B∩C)
(5)命題
①「p⇒qが真」⇔ P⊂Q
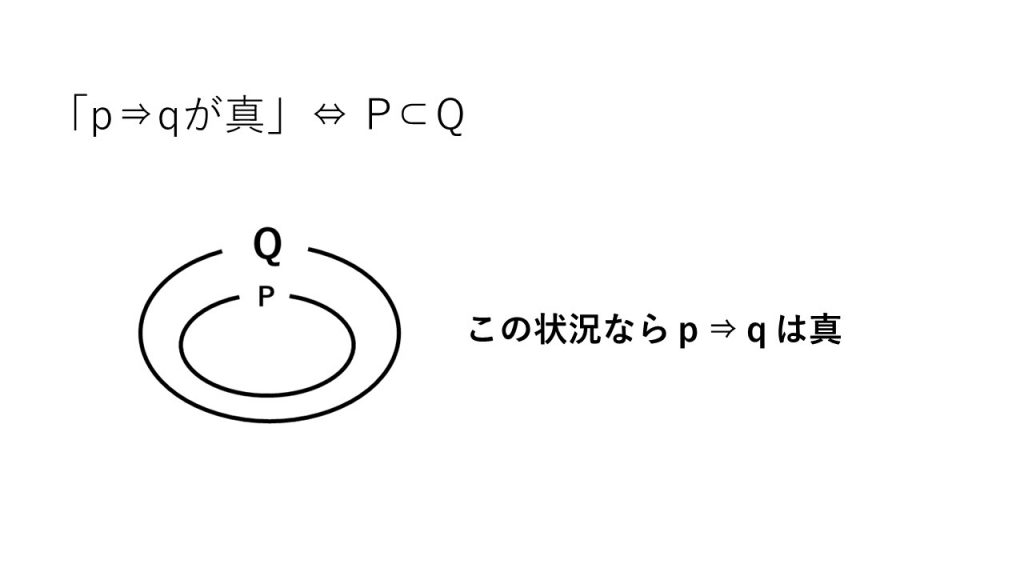
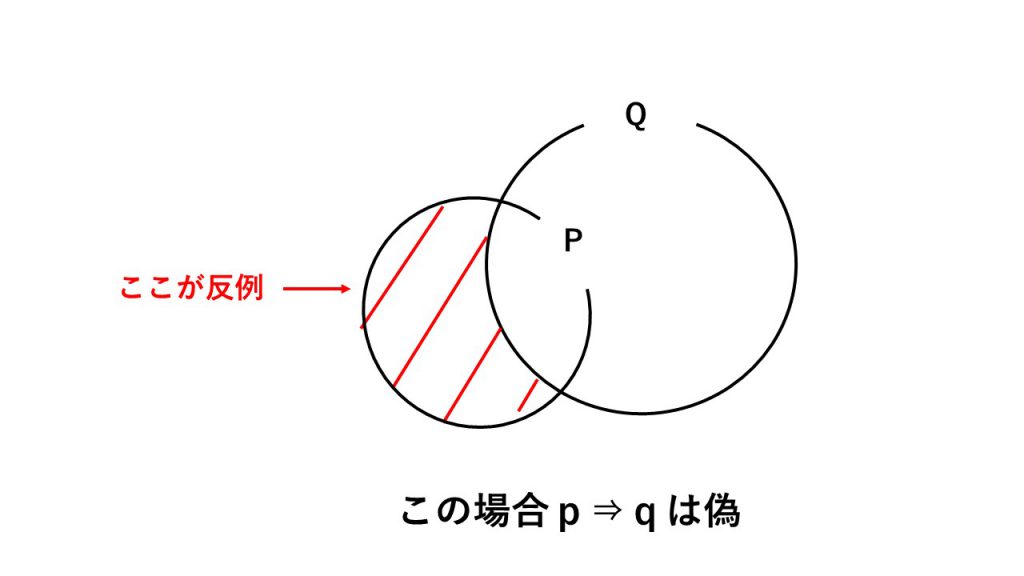
②反例の見つけ方
pならばqの反例:pを満たし、かつ、qを満たさないもの
③pはqであるための○○条件
・p⇒qが真:十分条件
・q⇒pが真:必要条件
・p⇒qが真、かつ、q⇒pが真:必要十分条件(同値)
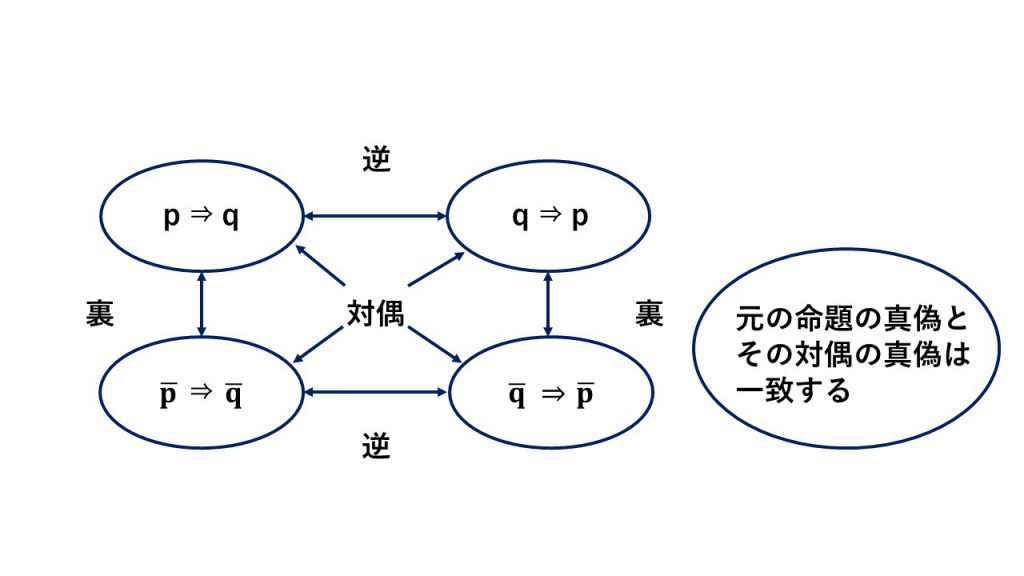
④対偶
(6)二次関数
→二次関数(二次方程式・二次不等式含む)の解説・授業・公式・演習問題一覧
①最大・最小を考えるときに縦に引く3つの線
→二次関数の最大と最小を考えるときに引くべき3つの線解説授業
ⅰ)定義域
ⅱ)定義域の中央
ⅲ)軸
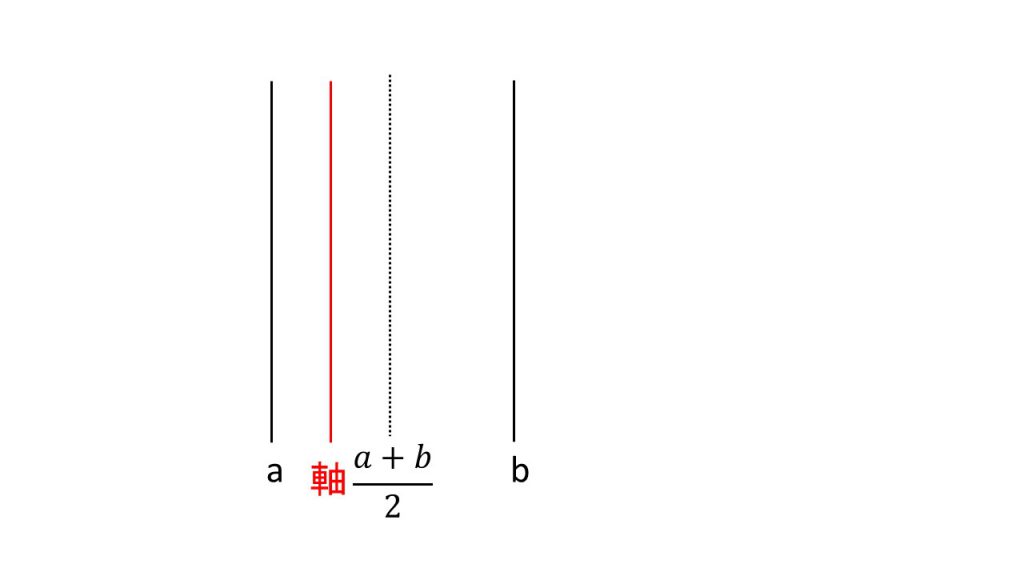
→ⅰ)~ⅲ)を引いた後、放物線をかけば、どこが最大・最小か分かるようになる。
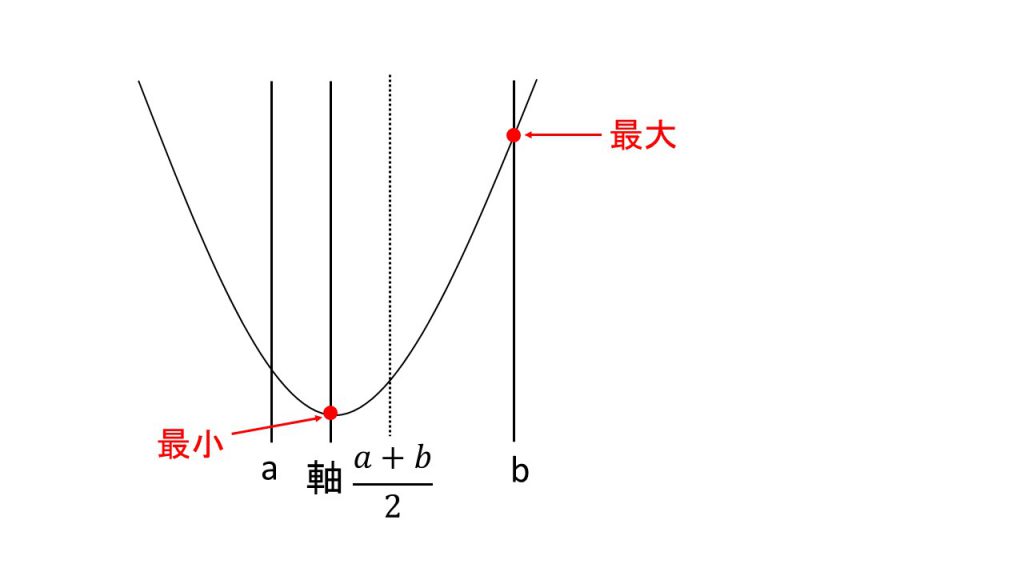
→二次関数の最大と最小を考えるときに引くべき3つの線解説授業
②場合分け
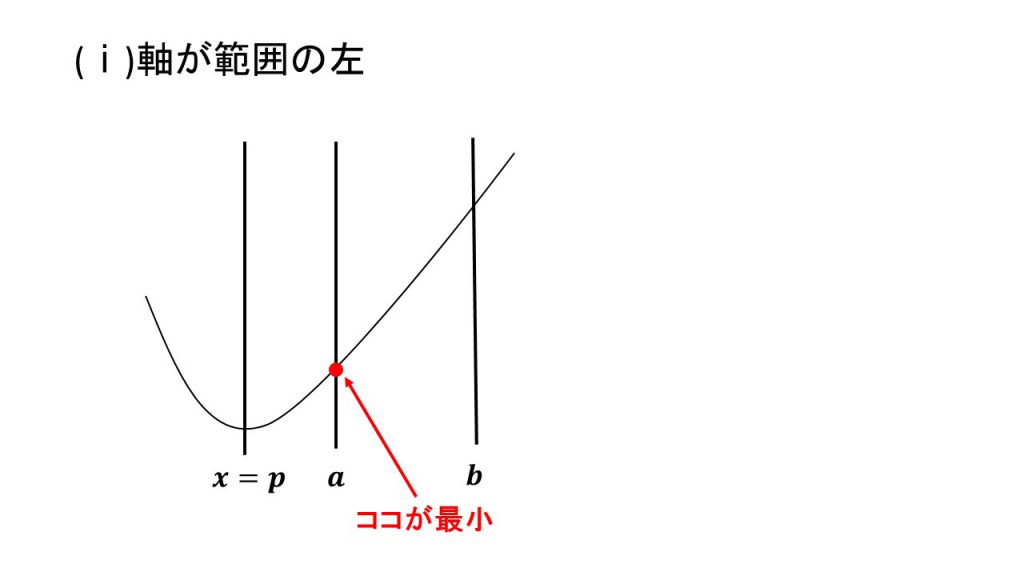
1.下に凸で最小値
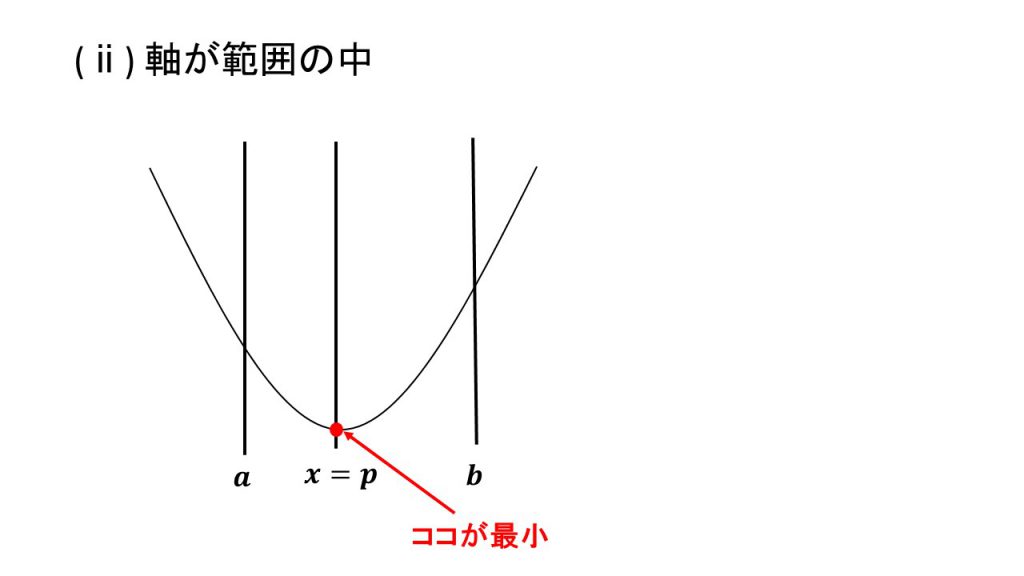
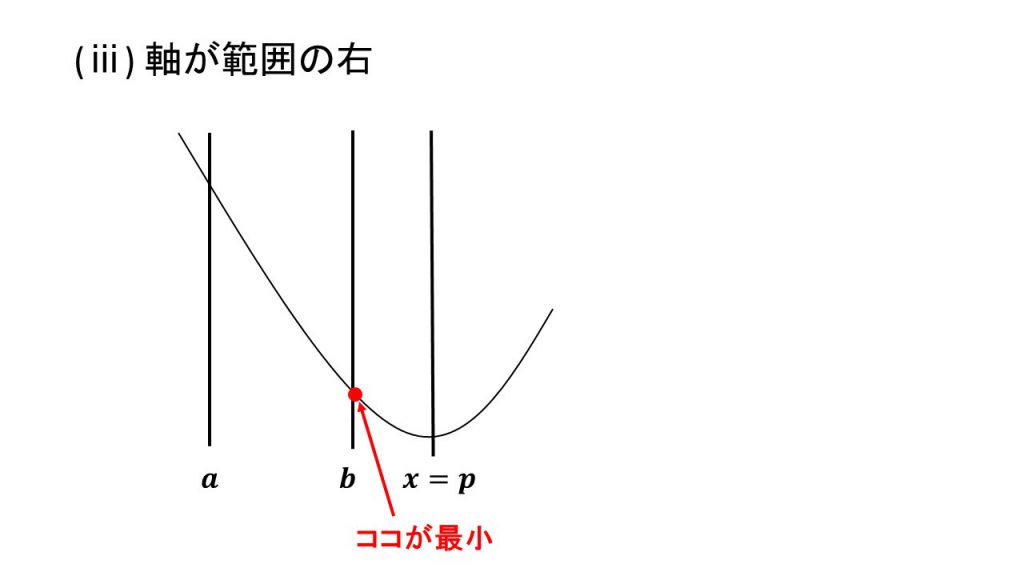
ⅰ)軸が範囲の左、ⅱ)軸が範囲の中、ⅲ)軸が範囲の右
2.下に凸で最大値
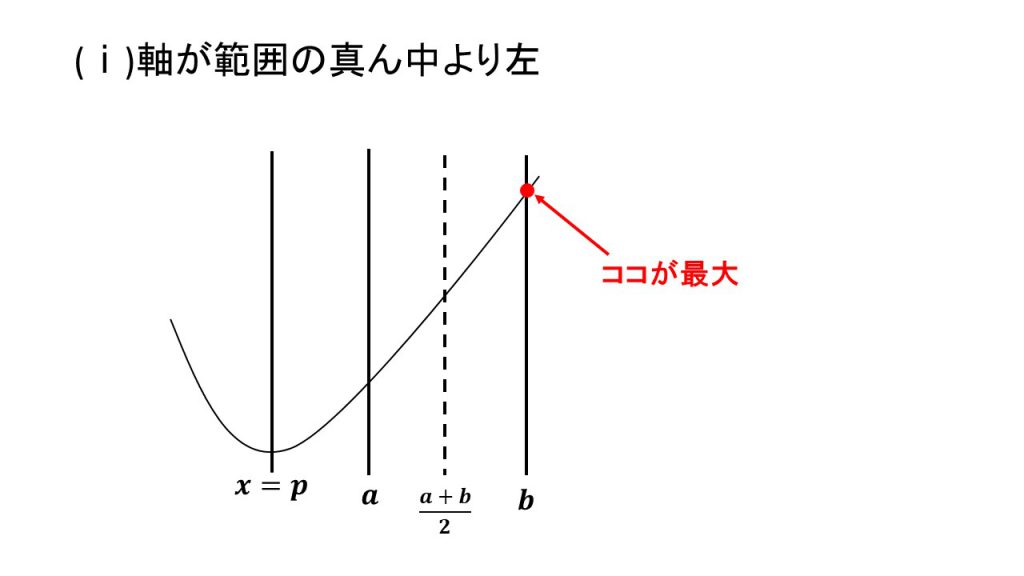
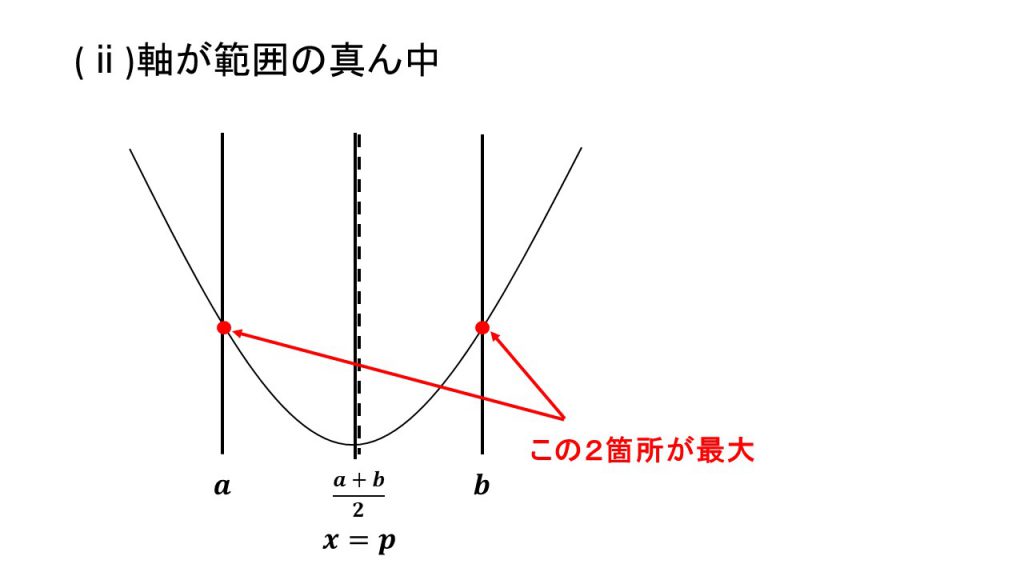
ⅰ)軸が範囲の真ん中より左、ⅱ)軸が範囲の真ん中と一致、ⅲ)軸が範囲の真ん中より右
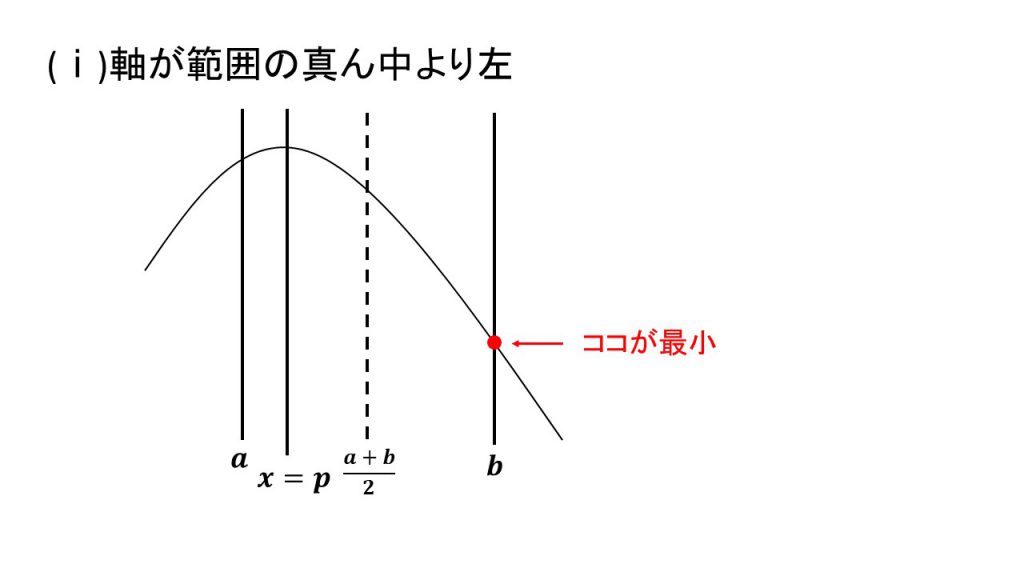
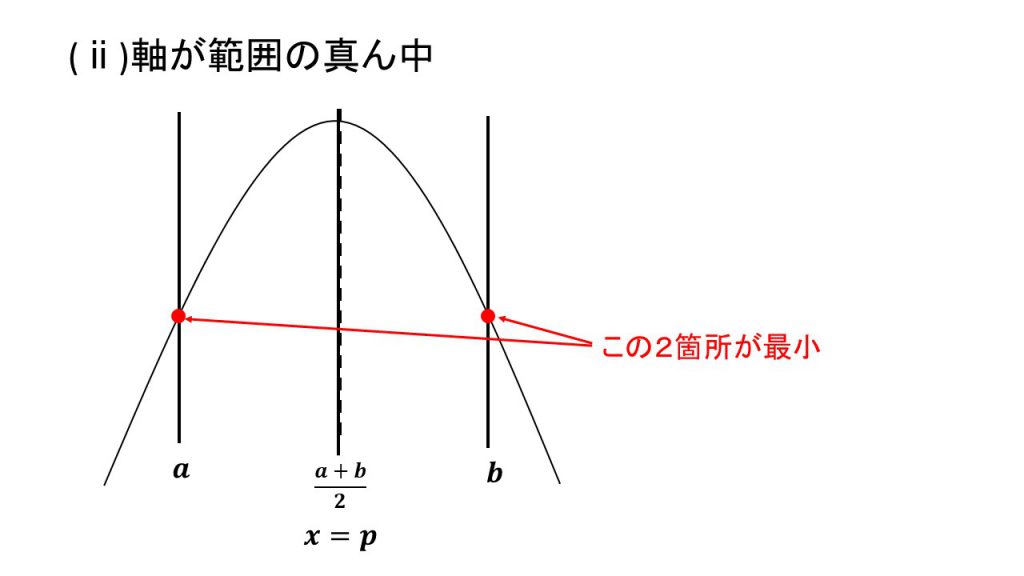
3.上に凸で最小値
ⅰ)軸が範囲の真ん中より左、ⅱ)軸が範囲の真ん中と一致、ⅲ)軸が範囲の真ん中より右
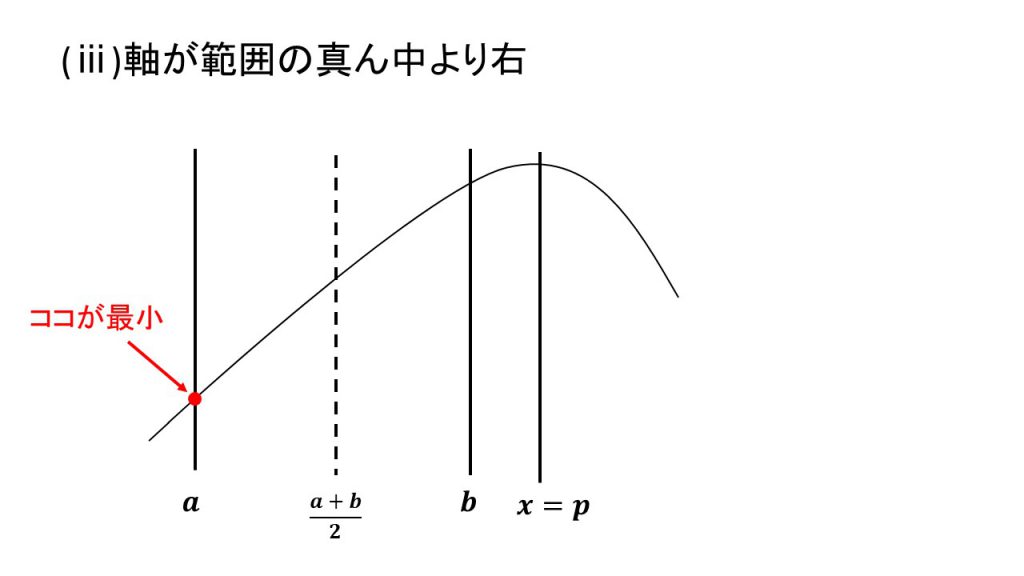
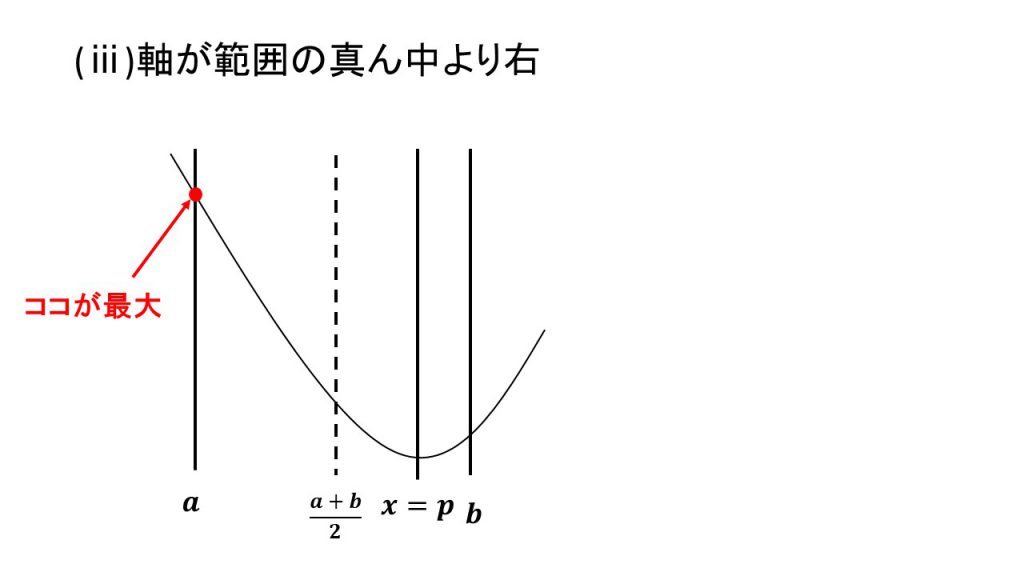
4.上に凸で最大値
ⅰ)軸が範囲の左、ⅱ)軸が範囲の中、ⅲ)軸が範囲の右
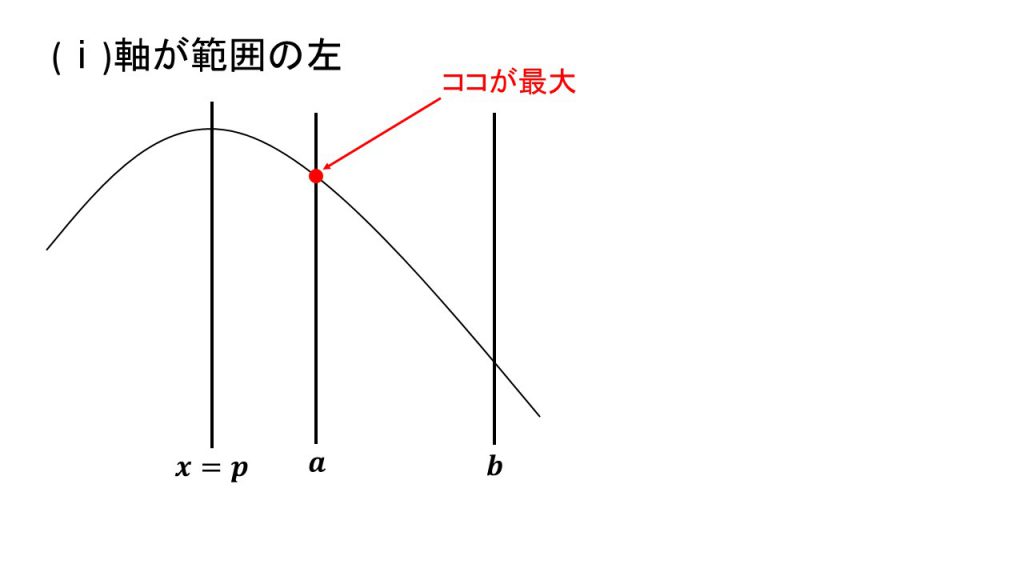
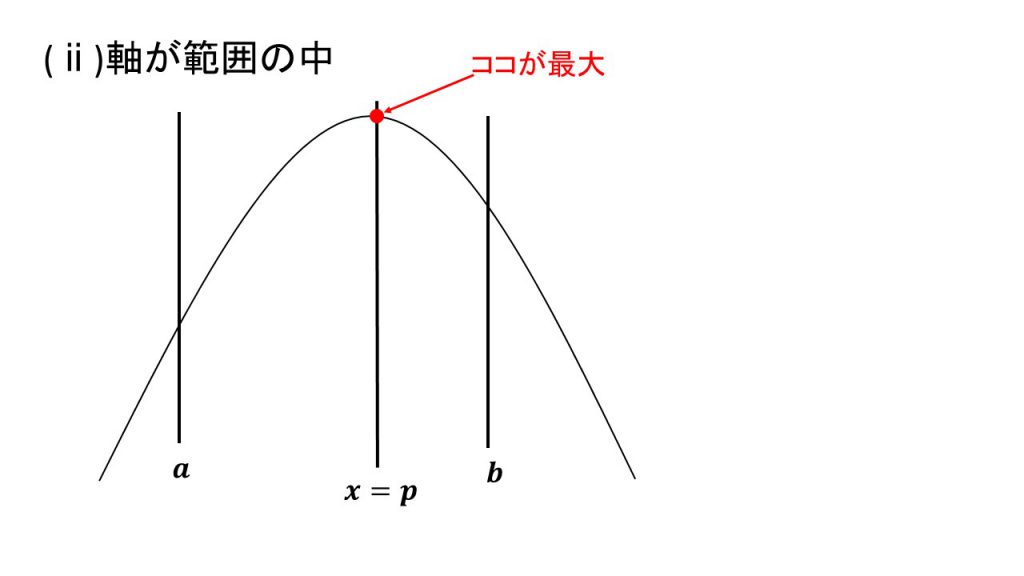
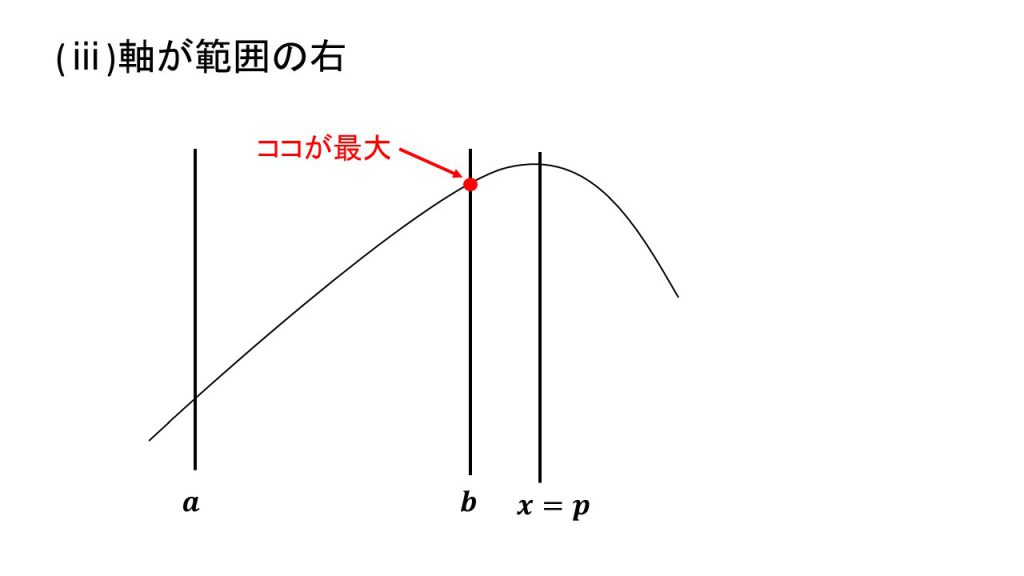
これらの場合分けの4パターンは覚えるというよりは、実際に3つの線と放物線をかいてみて理解するとよいでしょう。
③二次関数の決定で使う3つの式

④二次方程式の解の公式と判別式
-1024x576.jpg)
ⅰ)判別式が正のとき、異なる実数解が2つ
ⅱ)判別式が0のとき、実数解が1つ(重解)
ⅲ)判別式が負のとき、実数解はない(異なる虚数解が2つ)
⑤二次不等式の解法
ⅰ)左辺を因数分解できるときは因数分解する。因数分解できないときは、左辺=0の方程式を解の公式を利用して解く。
ⅱ)y=(左辺)のグラフがx軸よりも上か下かを考える。
⑥二次関数のグラフとx軸の交点の位置の問題で考えるべき3つの条件
ⅰ)判別式
ⅱ)軸
ⅲ)端点のy座標
(7)三角比
①直角三角形と三角比
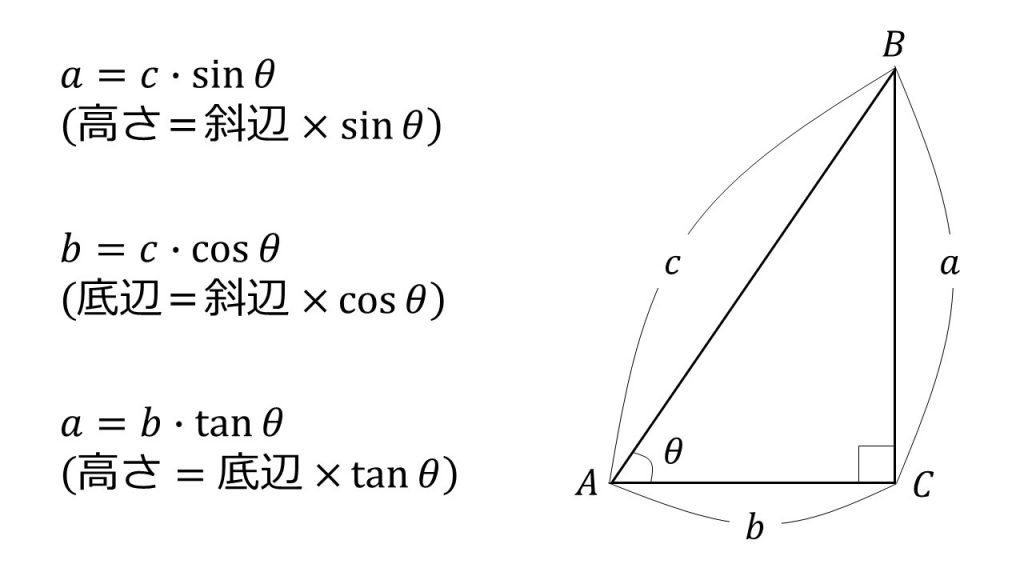
②三角比の相互関係の3つの式

③180°-θ、90°-θ、90°+θの三角比
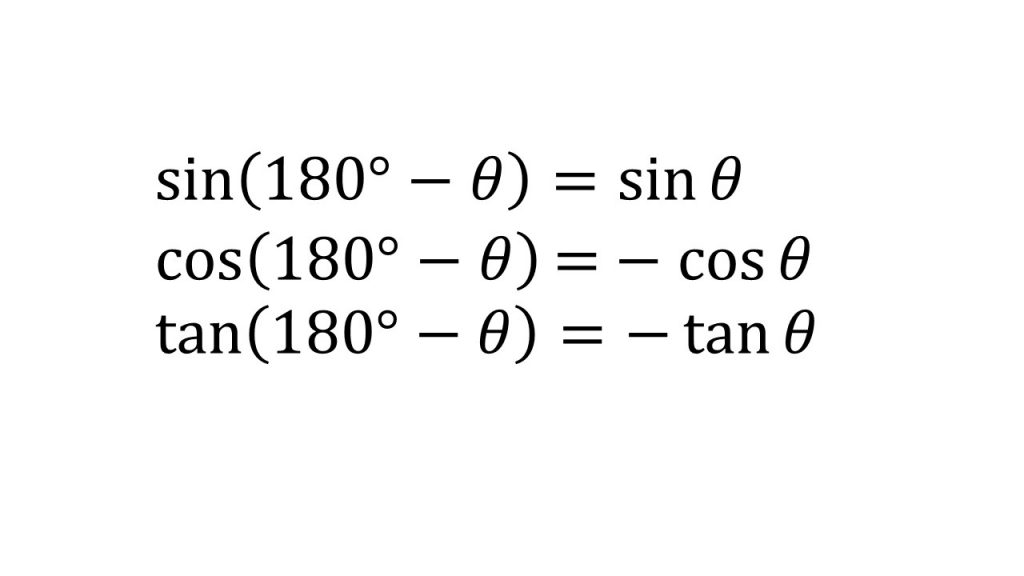
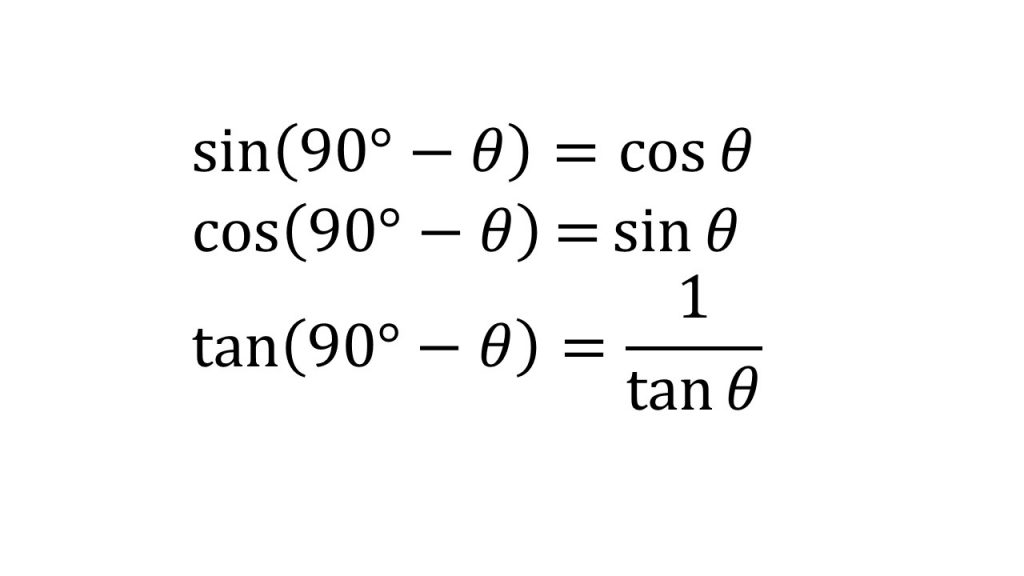
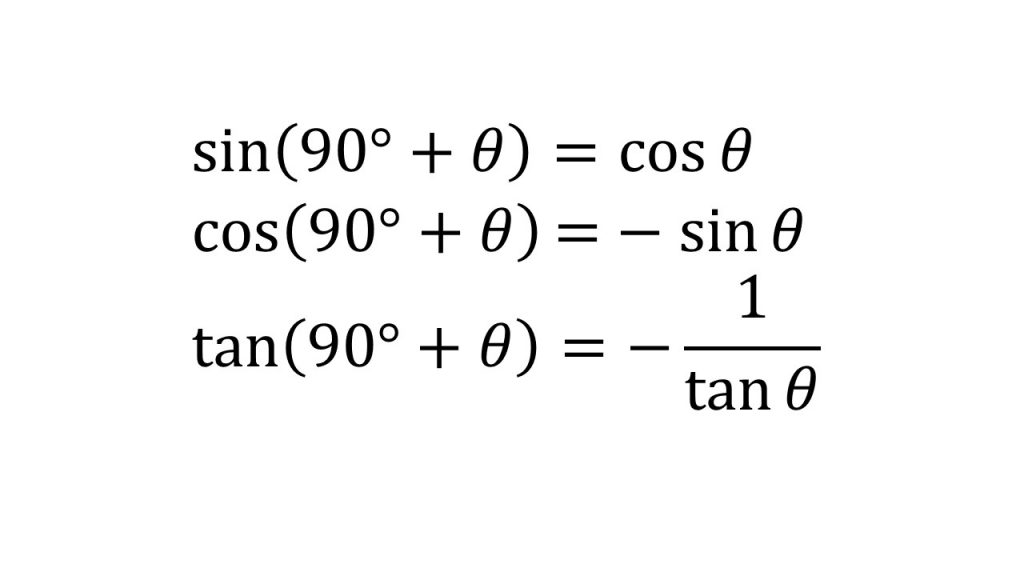
④正弦定理

⑤余弦定理

⑥三角形の面積の公式2つ

※問題文に「外接円の半径」と書いてあれば正弦定理、「内接円の半径」と書いてあれば三角形の面積の公式を使いましょう。
(8)データ分析
①四分位数
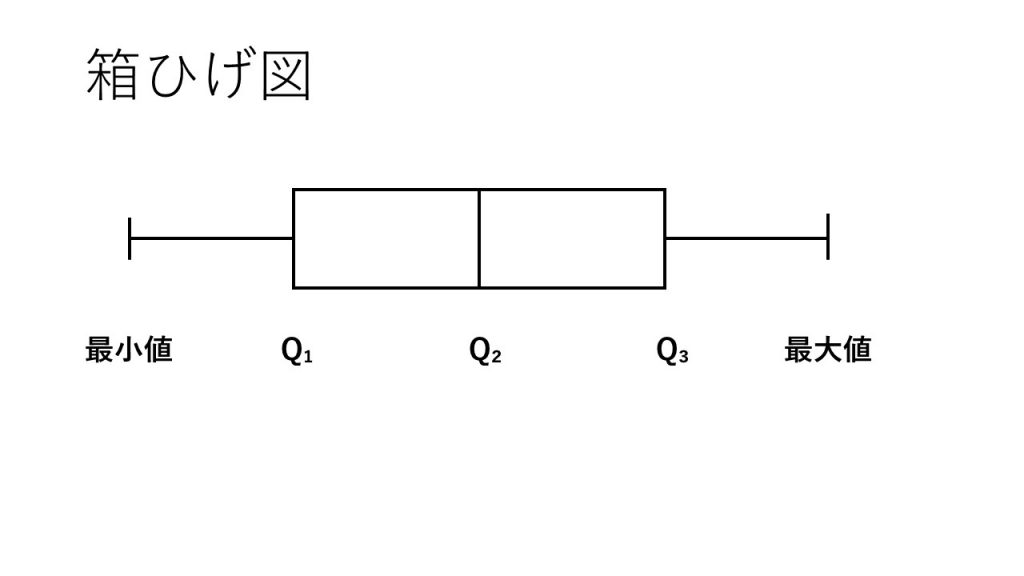
→データを小さい順に並べたときに4等分する位置にくる3つの値のこと
→小さい方から第1四分位数(Q₁)、第2四分位数(Q₂)、第3四分位数(Q₃)という。第2四分位数は中央値となる。
※四分位数の求め方
ⅰ)Q₂(中央値)を求める
ⅱ)Q₂を境目にして、下組と上組に分ける
ⅲ)下組の中央値がQ₁、上組の中央値がQ₃となる
②四分位範囲
Q₃-Q₁
③四分位偏差

※四分位偏差が大きい方がデータの散らばりが大きくなる。
④箱ひげ図
⑤平均

⑥分散

⑦標準偏差

⑧共分散

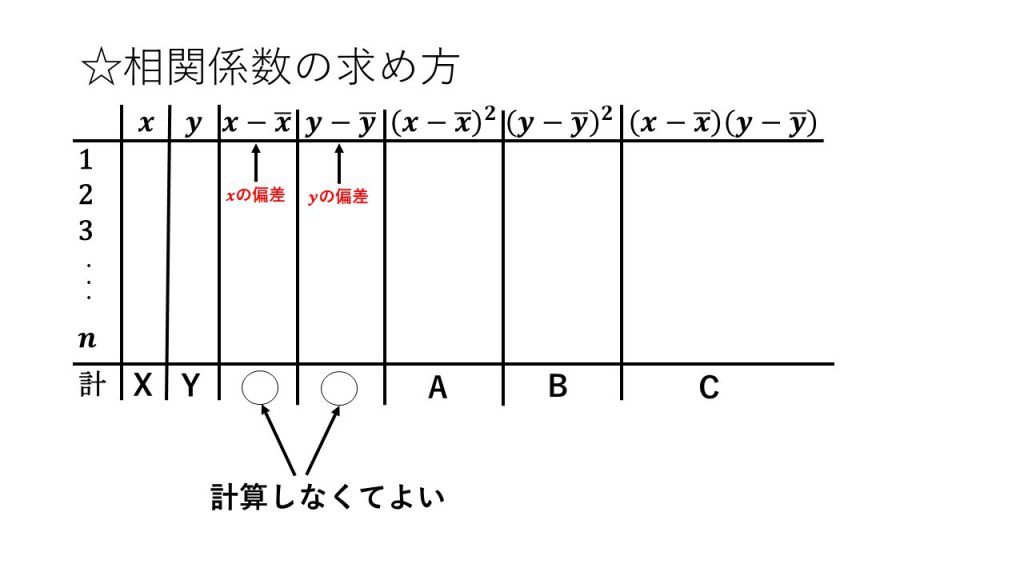
⑨相関係数

※表を用いた相関係数の求め方
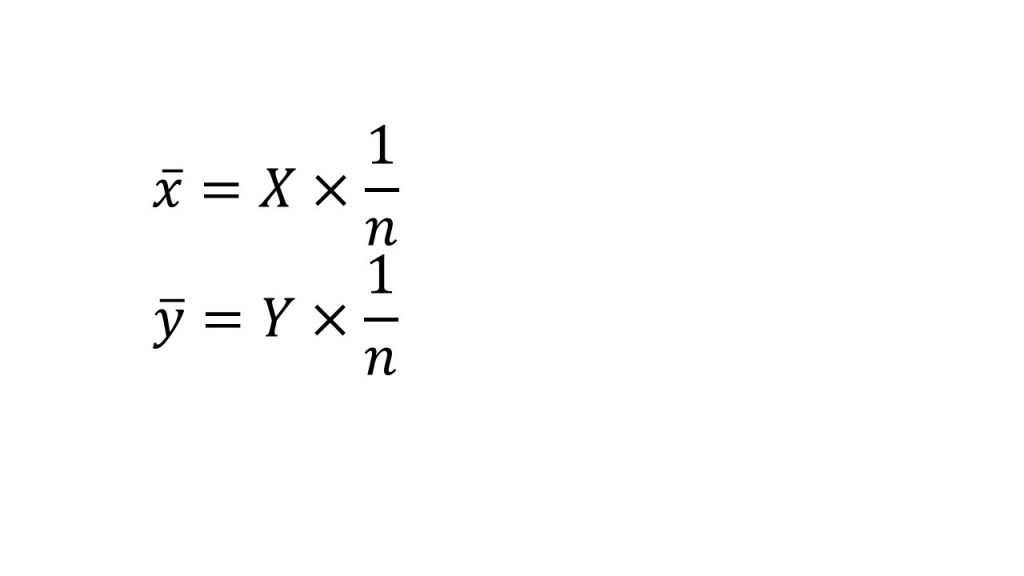
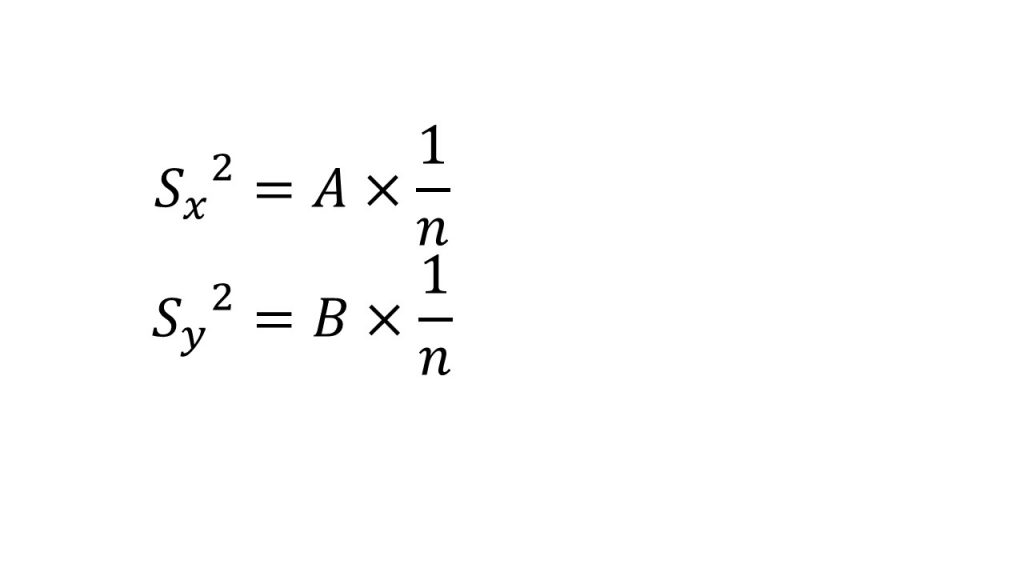
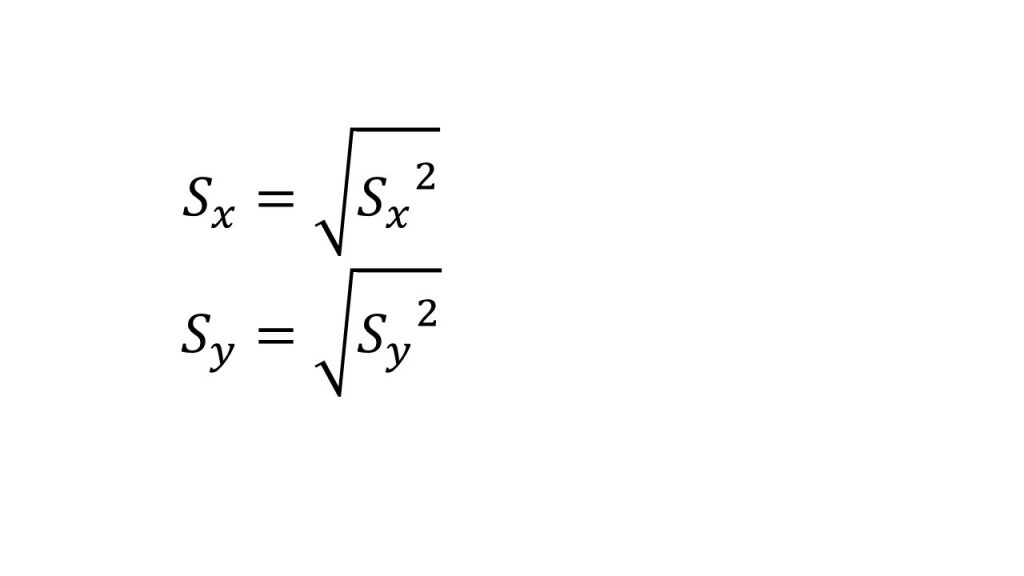
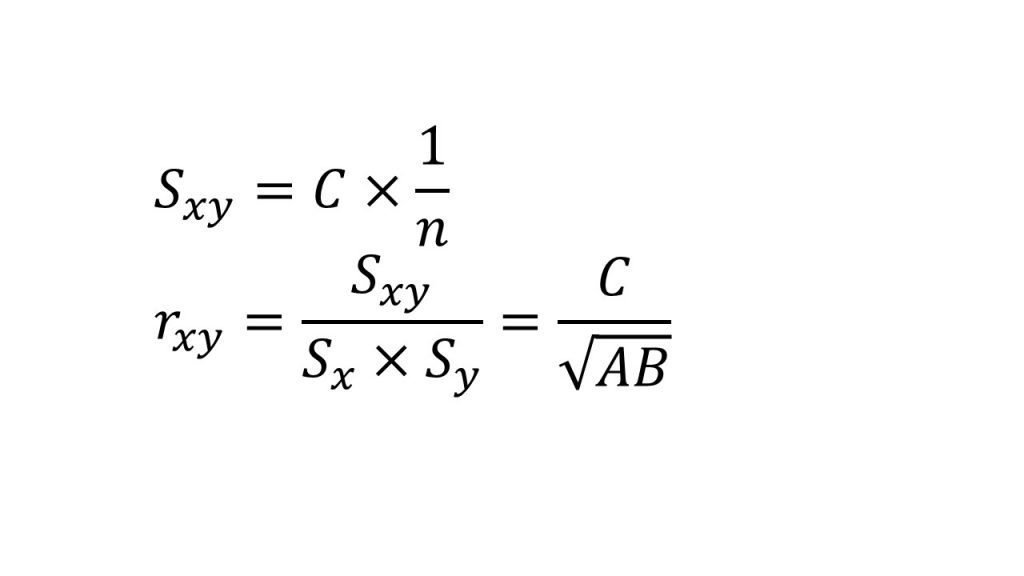
⑩変量の変換