(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
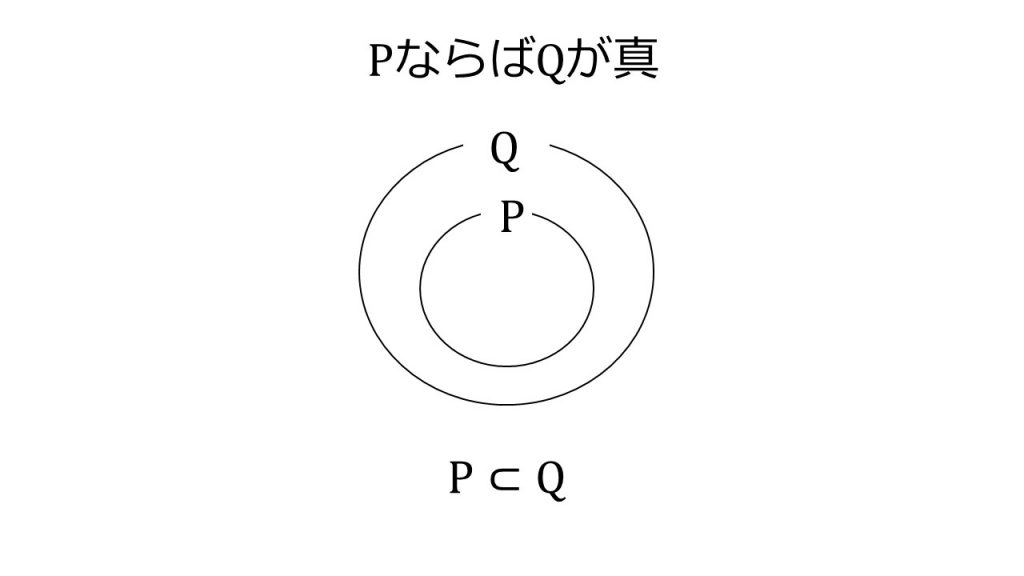
命題が真であるときの集合
例えば、「P⇒Q」(PならばQ)という命題が真であるとき、PとQの集合の関係はP⊂Qが成り立っています。
つまりQという集合の中にPという集合がすっぽり収まっていれば、「P⇒Qが真である」と言えます。
命題が偽であるときの集合(反例とは何か)
ちなみに、QとPの集合の関係でPがはみ出ている場合は、「P⇒Qは偽」となります。
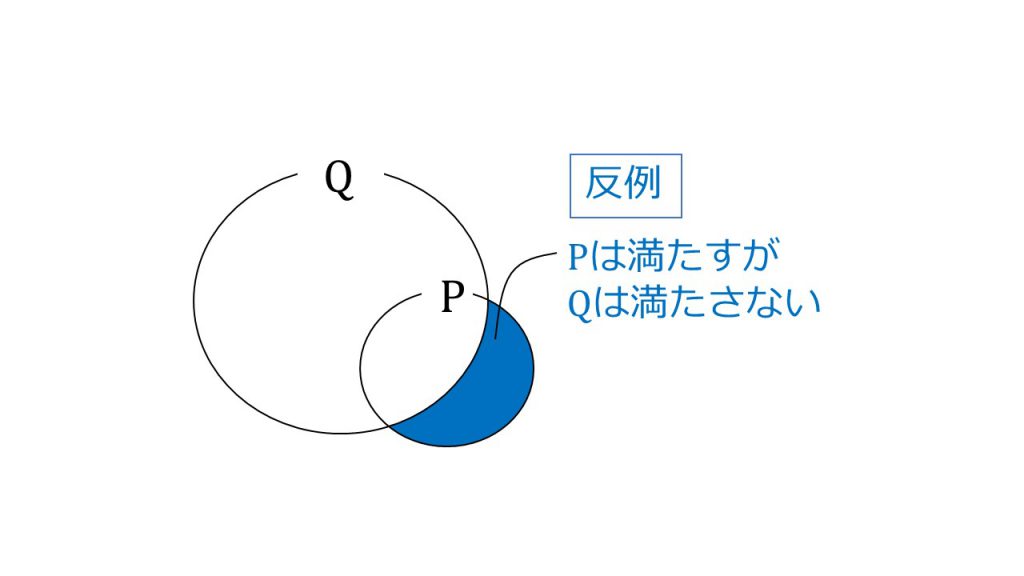
そして、このはみ出た部分を「反例」と呼んでいます。
すなわち、反例とは「Pは満たすがQは満たさない部分」、これが反例の定義です。そもそもPを満たさないものは反例にすらなることができないということは注意しておきましょう。
「自然数ならば整数である」は真か偽か
それではいくつか例題で確認してみます。例えば、
「自然数ならば整数である」
という命題があった場合、自然数と整数の関係は、整数の中に自然数がすっぽり収まっている関係なので、真となります。
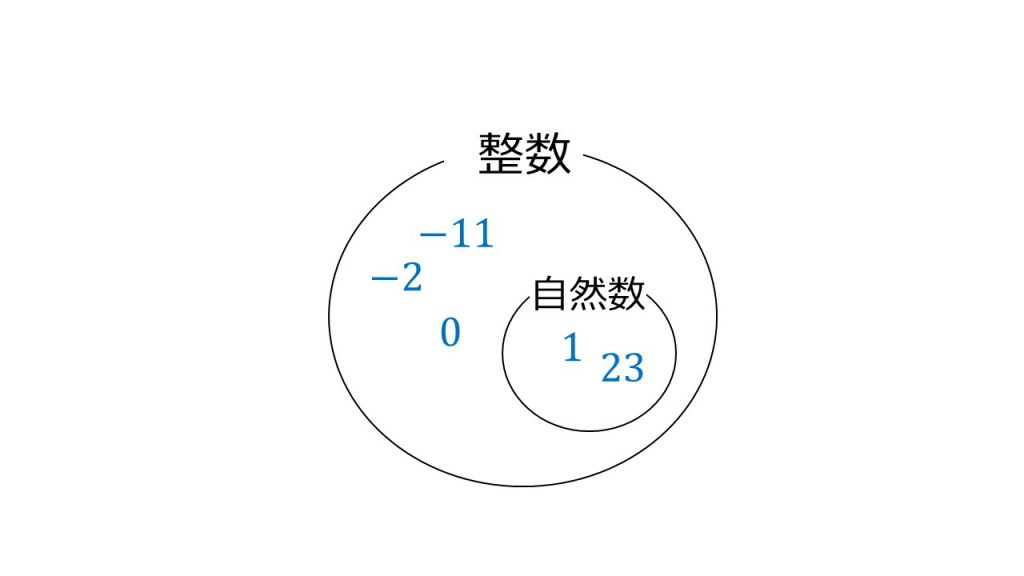
そのため、逆の「整数ならば自然数である」という命題は偽となります。例えば、-2や0などが反例となります。
※ちなみに、1.5などは「整数である」を満たしていないので、反例にすらなれない。
「平行四辺形ならば長方形である」は真か偽か
次に、
「平行四辺形ならば長方形である」
という命題ならばどうでしょうか。
この命題は偽となります。
なぜなら、平行四辺形の定義は2つの対辺が平行であることであり、長方形の定義は4つの内角が90 であることなので、平行四辺形と長方形の関係は、平行四辺形という集合の中に長方形がすっぽり収まっていることになります。

そのため、「平行四辺形であれば長方形である」は偽となり、逆の「長方形であれば平行四辺形である」という命題であれば、真となります。
同様にして、「正方形であれば長方形である」は真となりますが、「長方形であれば正方形である」は偽となります。
「0≦x≦2ならば|x|<2」は真か偽か
最後に、次の例題も考えてみます。
「0≦x≦2ならば|x|<2」
不等式が含まれた命題を考えるときは、数直線を書いて考えるようにしましょう。
|x|<2 ⇔ -2<x<2
なので、0≦x≦2と-2<x<2を数直線に書いて、|x|<2の中に0≦x≦2がすっぽり収まっているか考えてみましょう。

すると、-2<x<2の部分から、x=2の部分だけがちょうどはみ出ていることが分かります。つまり、このx=2が反例となるので、この命題は偽となります。
(3)解説授業の内容を復習しよう
(4)命題(数学Ⅰ)の解説一覧
②命題の真偽を集合で考えてみましょう!(命題の真偽と集合の関係、「P⇒Qが真」⇔「P⊂Q」)
