(1)例題
kを定数とする。自然数m, nに関する条件p, q, rを次のように定める。
p:m>k または n>k
q:mn>k2
r:mn>k
以下の( )に当てはまるものを、{必要条件であるが十分条件ではない・十分条件であるが必要条件ではない・必要十分条件である・必要条件でも十分条件でもない}から選べ。
①k=1とする。
pはqであるための( )
②k=2とする。
pはrであるための( )
③k=2とする。
pはqであるための( )
(2012年センター試験本試数学ⅠA第1問〔2〕より)
(2)例題の答案
①
p⇒qの対偶は、「mn≦1ならばm≦1かつn≦1」なので、m, nが自然数であることを考えれば対偶は真。よってp⇒qも真。
q⇒pの対偶は、「m≦1かつn≦1ならばmn≦1」なので、対偶は真。よってq⇒pも真。
したがって、pはqであるための必要十分条件である。
②
p⇒rの対偶は、「mn≦2ならばm≦2かつn≦2」なので、対偶は真。よってp⇒rも真。
r⇒pの対偶は、「m≦2かつn≦2ならばmn≦2」なので、対偶は偽(反例:m=2, n=2)。よってr⇒pも偽。
したがって、pはqであるための十分条件であるが必要条件ではない。
③
p⇒qの対偶は、「mn≦4ならばm≦2かつn≦2」なので、対偶は偽(反例:m=4, n=1)。よってp⇒qも偽。
q⇒pの対偶は、「m≦2かつn≦2ならばmn≦4」なので、対偶は真。よってq⇒pも真。
したがって、pはqであるための必要条件であるが十分条件ではない。
(3)解法のポイント
P→Qが真のとき十分条件、Q→Pが真のとき必要条件となります。
解法の手順としては、
①P→Qの真偽を確かめる
②Q→Pの真偽を確かめる
のように分けて順番に考えるようにしてください。
真偽は集合で考えたほうがやりやすい場合が多いです(特に不等式がある場合)
また、真偽を確かめるときに、そのままではやりにくい場合は対偶を利用してみましょう(対偶の真偽は元の命題の真偽と一致する)
「〜ない」「少なくとも〜」「〜または……」などがあった場合は、対偶をとるとうまくいくことが多いです。
(4)必要な知識
①「p⇒qが真」⇔ P⊂Q
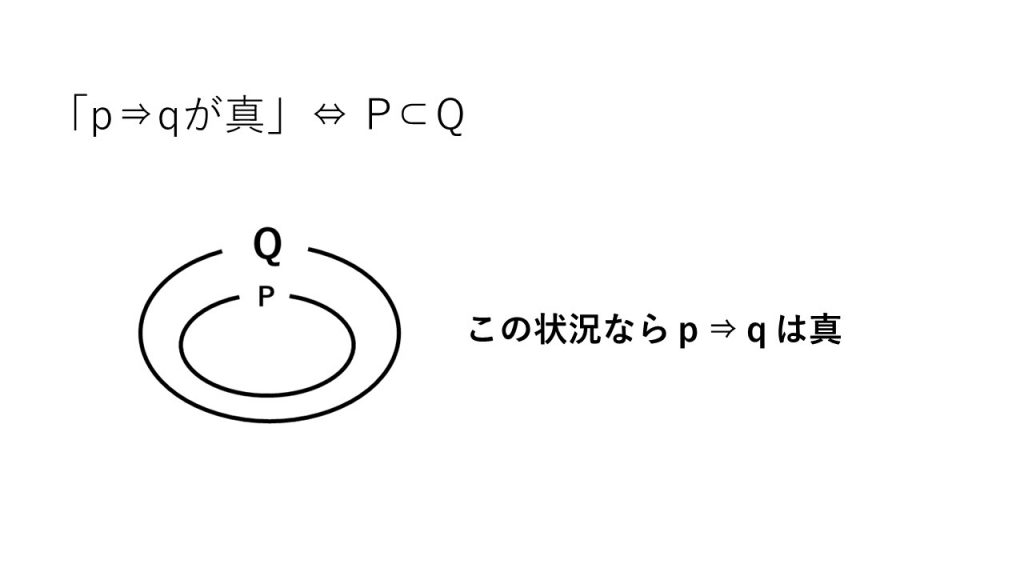
②反例の見つけ方
→pならばqの反例:pを満たし、かつ、qを満たさないもの
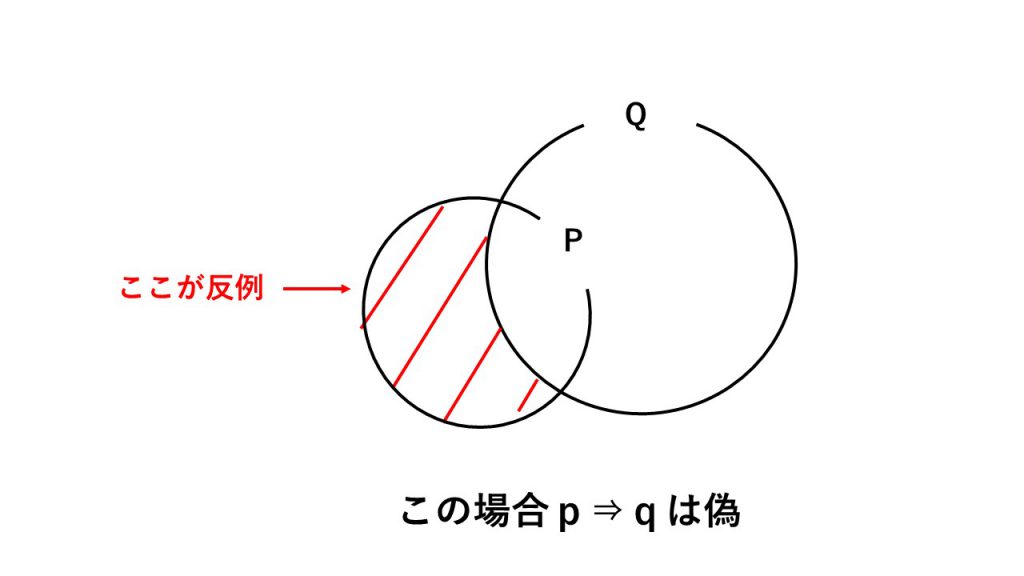
③pはqであるための○○条件
・p⇒qが真:十分条件
・q⇒pが真:必要条件
・p⇒qが真、かつ、q⇒pが真:必要十分条件(同値)
④対偶
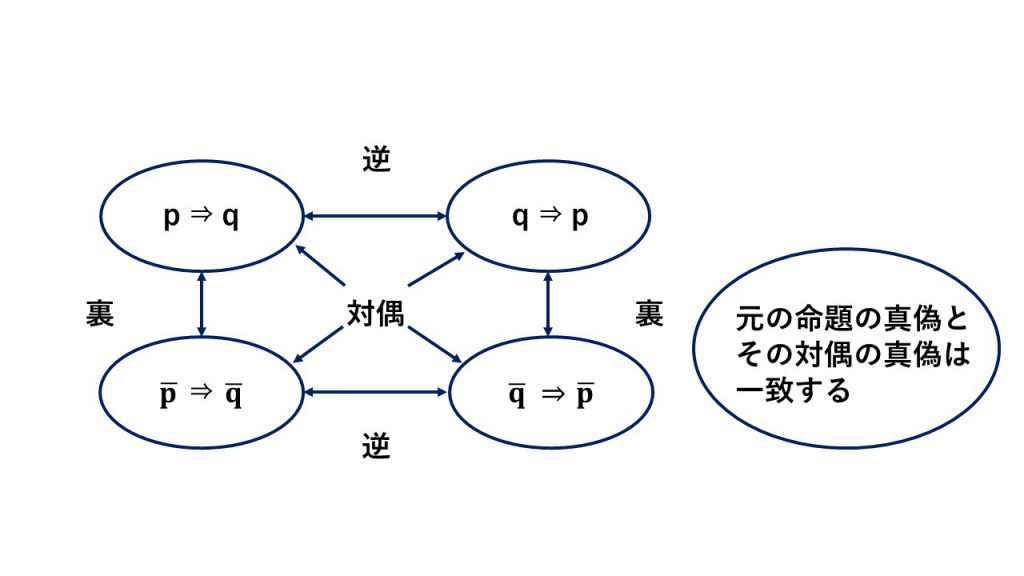
命題の真偽を考えるときのコツを理解しましょう→命題の真偽を集合で考えてみましょう!(命題の真偽と集合の関係、「P⇒Qが真」⇔「P⊂Q」)
