(1)解説授業動画
- 次:漸化式をマスターしよう(2)基本パターン⑧(最も重要なパターン、これが理解できたら漸化式の基本はマスターしたと言えます)
- 前:漸化式をマスターしよう(2)基本パターン⑥(和Snが与えられているパターン、なぜn≧2としなければいけないのか)
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
それでは次はan+1=an+f(n)のパターンの漸化式を解きます。
f(n)は階差数列
このパターンの漸化式のポイントは、anの係数が1になっていることです。anの係数が1になっていればf(n)は階差数列となります。
なぜならこのパターンの漸化式は
an+1−an=f(n)
の形に式変形することができ、この式は、ある項からその前の項を引けばnを含んだ式f(n)、つまりなんらかの数列となっているということを意味しているからです。
よって、このf(n)が階差数列であると分かれば、

この階差数列を使った公式を使うことができます。階差数列を使った公式がなぜこのようになるかは、別の動画で解説しているので、ぜひそちらもご覧になってください。
特に注意したいのが、Σの上がn−1になっていることです。この公式はn−1を扱っているので、和が与えられているパターンと同様に、n≧2のときしかこの公式は使えません。
例題で解法を確認
以上の点に注意して、a1=1、an+1=an+3n2−4nの漸化式を解いてみます。
まずはanの係数を見ます。今回はanの係数が1になっているので、3n2−4nはanの階差数列になります。したがって、答案は以下のようになります。

まずは必ずn≧2を記述して、階差数列の公式を使います。Σの上をn−1にするのを忘れないようにしましょう。また、Σの中の(3k2-4k)をnで書いてしまう人がよくいるのですが、必ずΣの下の文字と合わせてkで書くようにしましょう。
あとは、このΣの計算をしていきます。Σは分配法則が成り立つので、
Σ(3k2-4k)=3Σk2-4Σk
のように分配し、
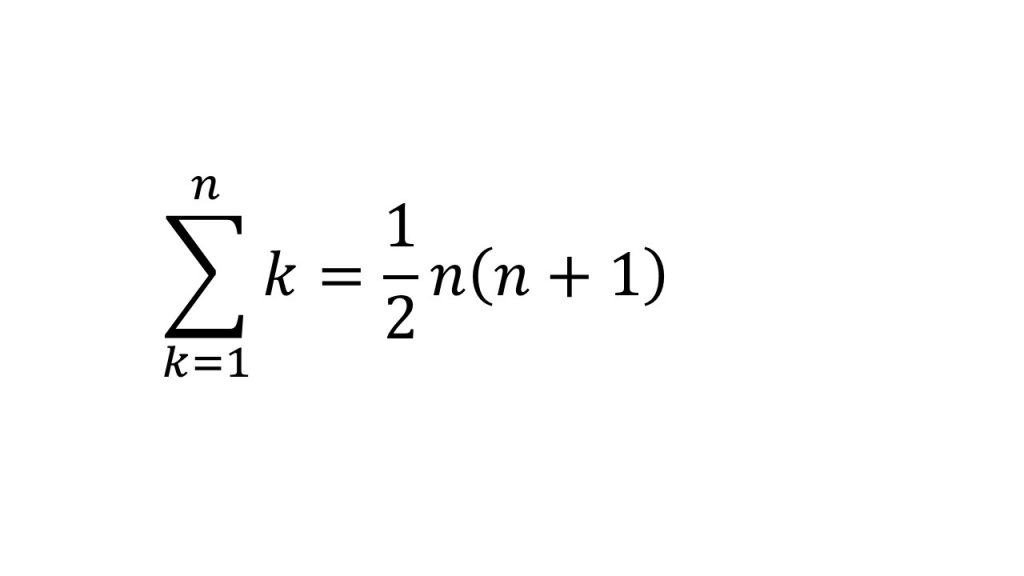
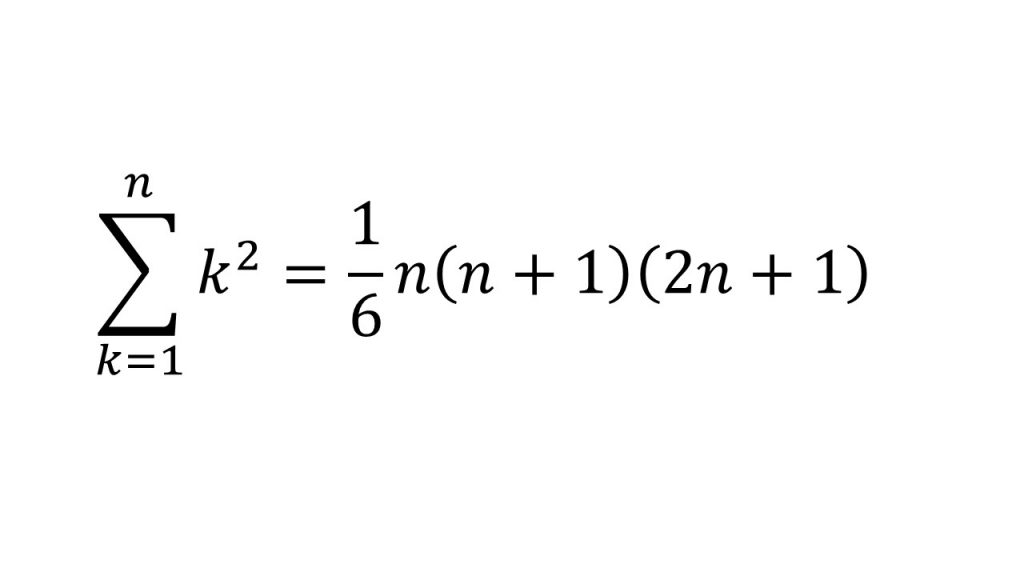
これらの公式を使っていきます。ただし、これらの公式を使うときに注意しなきゃいけないのは、Σの上がn−1になっているので、この2つの公式のnをn−1にしないといけません。それらに気をつけて計算すると、
an=1+3・1/6(n−1)・n・(2n−1)−4・1/2(n−1)・n
となります。
ここからの計算にもポイントがあり、全て展開して整理しようとするのではなく、まず分数でくくるようにしましょう。今回でいえば、約分をしたあとに3・1/6(n−1)・n・(2n−1)と、4・1/2(n−1)・nの項に1/2が残るので、全体を1/2でくくります。そうすると、1は2倍して2となり、真ん中の項+3・1/6(n−1)・n・(2n−1)は1/2が外に出て、最後の項−4・1/2(n−1)・nも2倍して係数が4となり、まとめると、
1/2{2+(n−1)・n(2n−1)−4(n−1)・n}
になります。このように分数で全体をくくると分数の計算をしなくてよくなるので、計算ミスが減り、正確にかつ速く計算することができるようになります。
最後にカッコの中を整理すると、an=1/2(2n3−7n2+5n+2)のようになります。
そして、ここで答えとしてはいけません。なぜなら、最初からここまではあくまでもn≧2のときの話をしているので、n=1のときもan=1/2(2n3−7n2+5n+2)が成り立つかは示されていないからです。
よって、n=1のときもこれが成ち立つことを確認するために、an=1/2(2n3−7n2+5n+2)の右辺にn=1を代入して計算してみます。そうすると、
1/2(2・1−7・1+5・1+2)=1
となるので、問題文で与えられているa1=1と、1/2(2n3−7n2+5n+2)のnに1を入れたものが一致するので、an=1/2(2n3−7n2+5n+2)はa1=1のときも成り立つことが分かります。よって、すべての自然数nにおいて、an=1/2(2n3−7n2+5n+2)となります。
(3)解説授業の内容を復習しよう
(4)漸化式基本パターン解説一覧
①漸化式をマスターしよう(2)基本パターン①(特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義)
②漸化式をマスターしよう(2)基本パターン②(n乗の項を含む漸化式)
③漸化式をマスターしよう(2)基本パターン③(分母と分子にanを含む漸化式)
④漸化式をマスターしよう(2)基本パターン④(anan+1を含む漸化式)
⑤漸化式をマスターしよう(2)基本パターン⑤(anにルートや指数がついている漸化式)
⑥漸化式をマスターしよう(2)基本パターン⑥(和Snが与えられているパターン、なぜn≧2としなければいけないのか)
⑦漸化式をマスターしよう(2)基本パターン⑦(階差数列の公式を使うパターン)
⑧漸化式をマスターしよう(2)基本パターン⑧(最も重要なパターン、これが理解できたら漸化式の基本はマスターしたと言えます)
(5)漸化式をマスターしよう(数学B)の解説一覧
②漸化式をマスターしよう(1)基本中の基本(等差数列の漸化式、等比数列の漸化式、そもそも漸化式とは何か)
④漸化式をマスターしよう(3)応用パターン解説(隣接3項間漸化式、発想が難しい漸化式、一般項を予想して数学的帰納法で証明するパターン)
(6)参考
☆漸化式(数学B)をマスターしよう(漸化式全パターンの解説・授業・演習問題一覧)
☆数学の解説・授業・公式・演習問題一覧(Ⅰ・A・Ⅱ・B・Ⅲ)
「漸化式をマスターしよう」シリーズは、『細野真宏の数列と行列が面白いほどわかる本 Version2.0』(細野真宏著、(株)中経出版発行、現在は絶版)を参考にしています。
細野真宏先生が現在発行している出版物はこちら(小学館HP)→https://www.shogakukan.co.jp/author/5885
中経出版の参考書・問題集はこちら(学参ドットコム)→https://www.gakusan.com/
