(1)平面ベクトル
①始点をそろえる

②単位ベクトル

③ベクトルの平行条件

④3点が一直線上にある条件

⑤ベクトルの成分
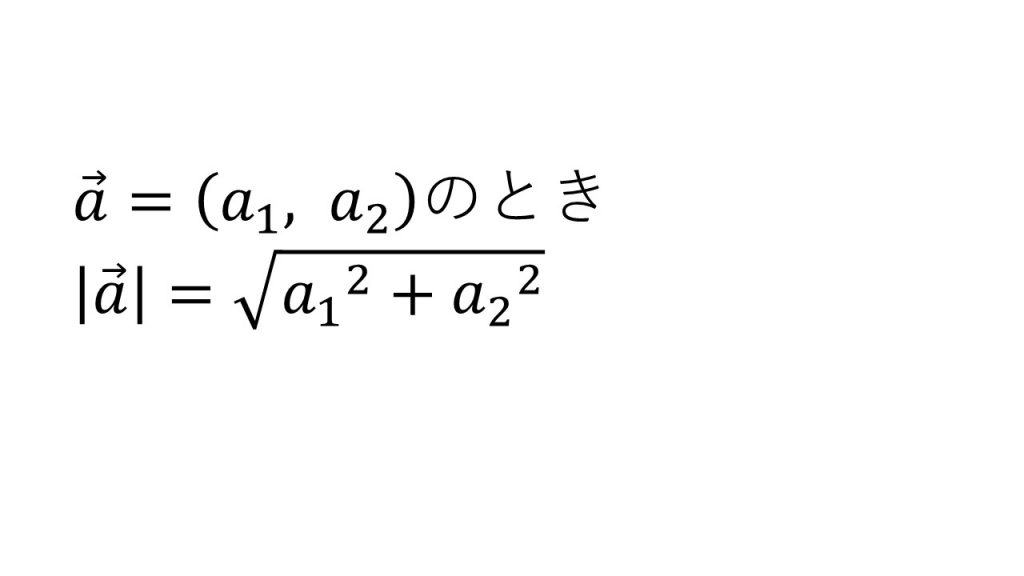
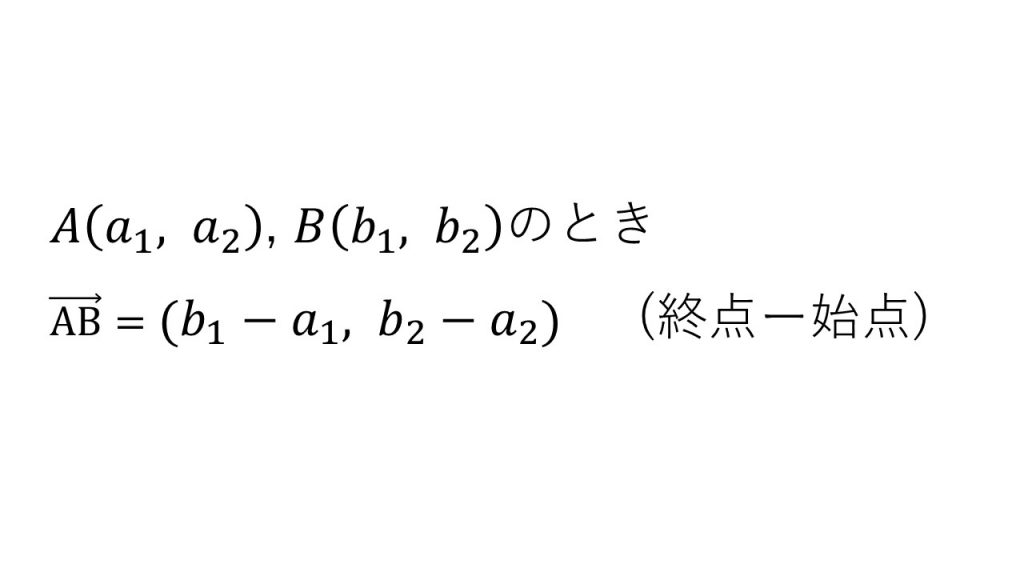
⑥内積
ⅰ)内積の定義

ⅱ)成分による内積

⑦ベクトルの垂直条件
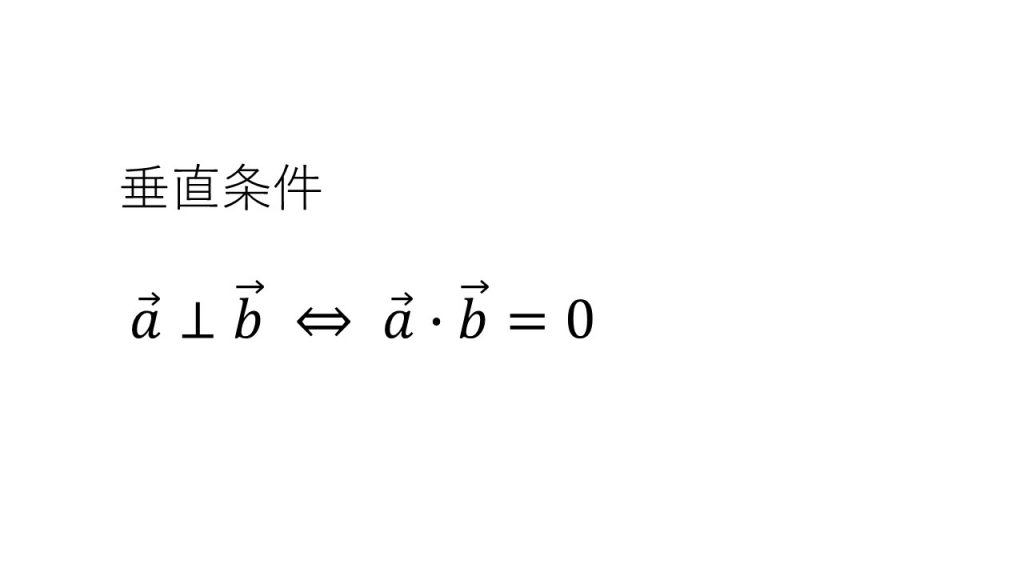
⑧位置ベクトルの定義

⑨内分の位置ベクトル

⑩外分の位置ベクトル

⑪中点の位置ベクトル

⑫重心の位置ベクトル

⑬ベクトルを使った三角形の面積の公式

(2)ベクトル方程式
①直線のベクトル方程式3パターン



②円のベクトル方程式2パターン


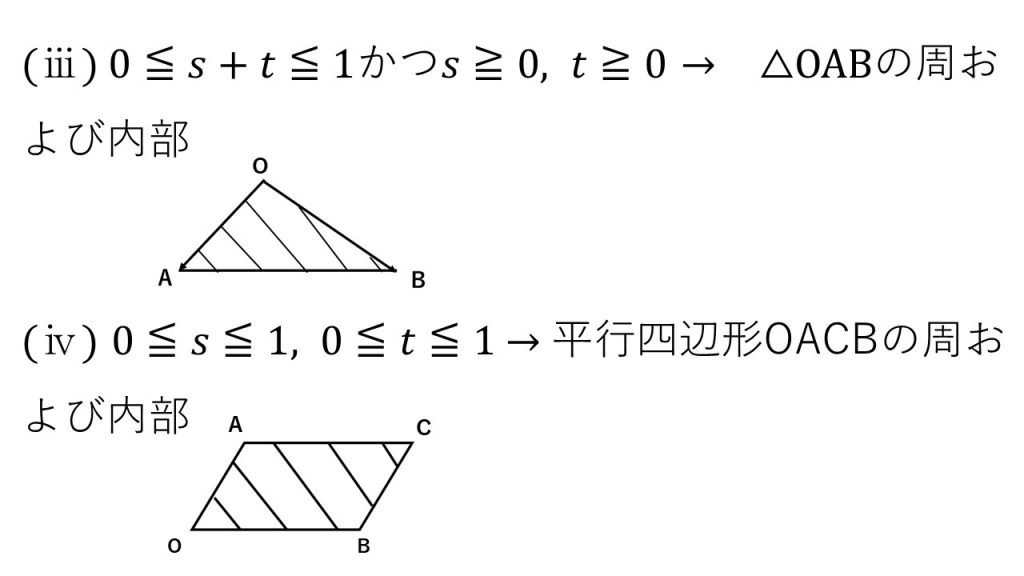
③終点の存在範囲基本4パターン

(3)空間ベクトル
☆基本は平面ベクトルと同じ。成分が3つに増えただけだと考えよう。
①共面条件(4点が同一平面上にある条件)

(4)数列
①等差数列


②等比数列

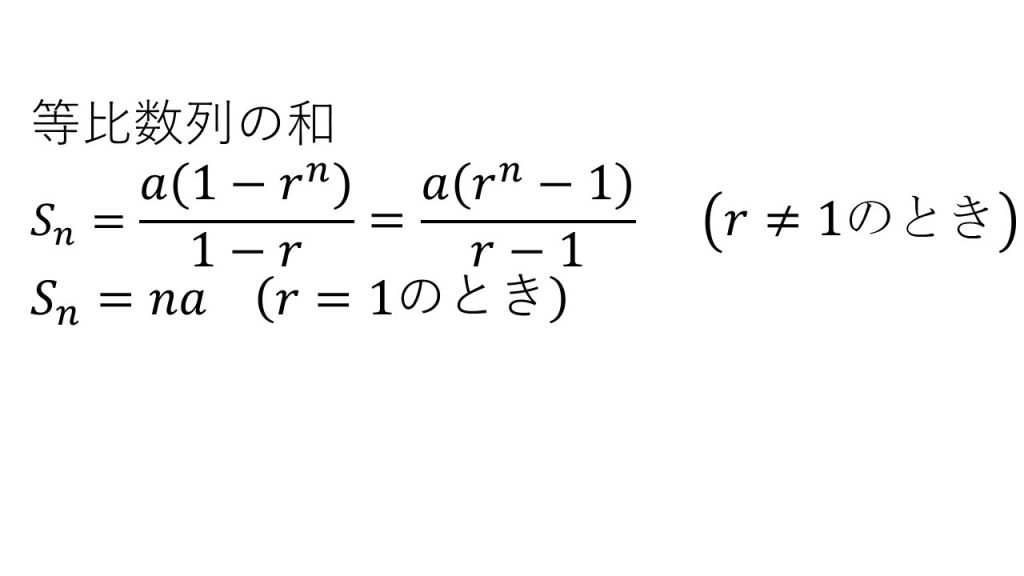
③Σの定義
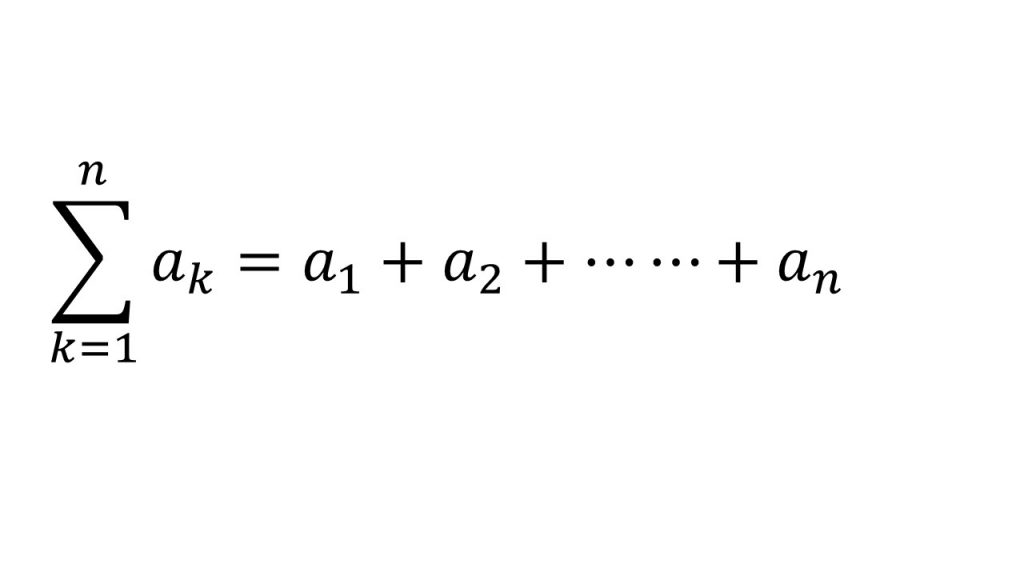
④Σの計算
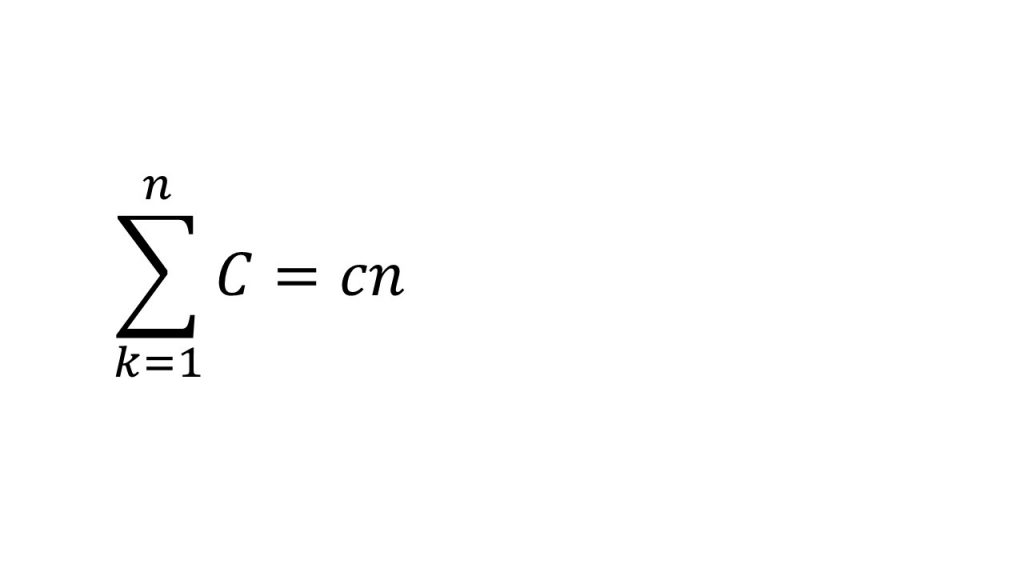
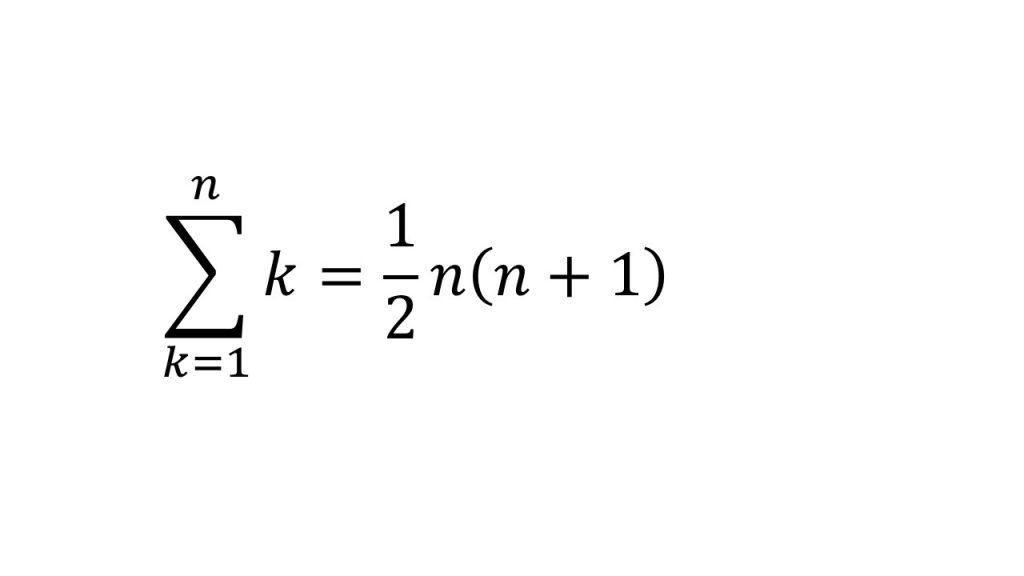
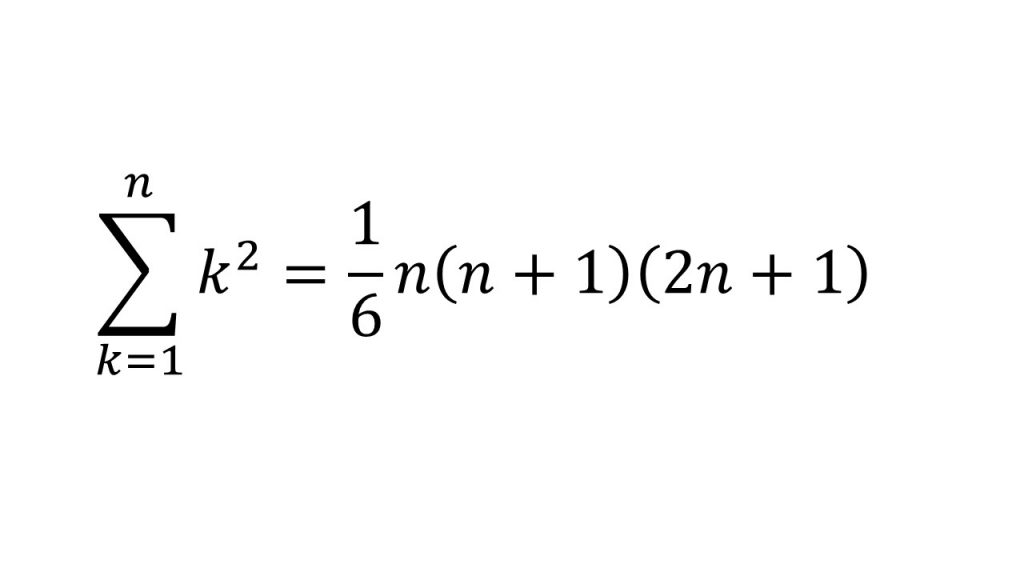
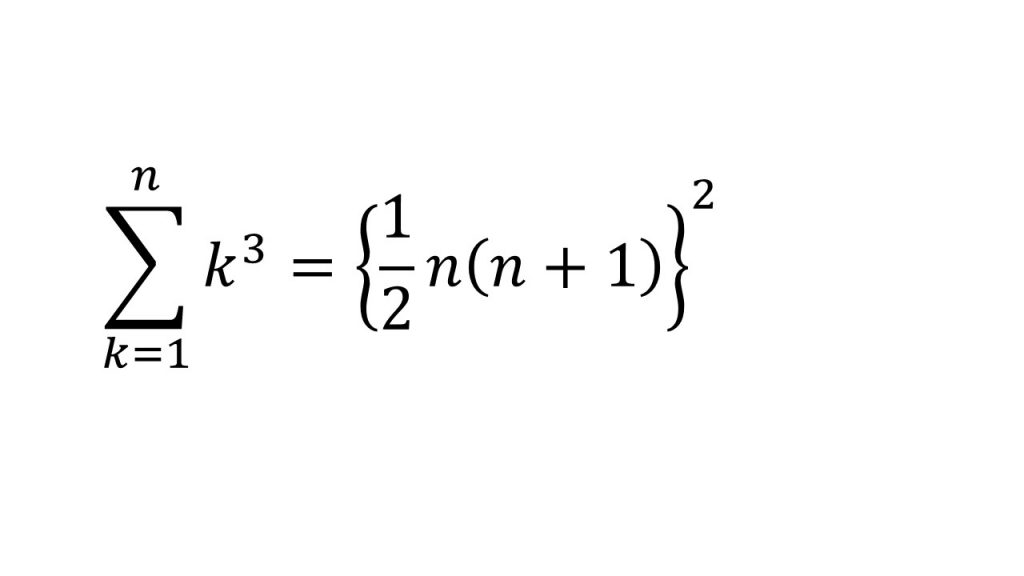

⑤階差数列

⑥数列の和から一般項を求める

⑦分母に積の形がある分数の数列の和
→部分分数分解
※部分分数分解のやり方はこちら→部分分数分解のやり方
⑧(等差数列)×(等比数列)の和
→公比をかけて、ずらして引く
(5)数学的帰納法
①等式
→数学的帰納法の分かりやすい答案の書き方(等式バージョン)解説授業

②不等式
→数学的帰納法の分かりやすい答案の書き方(不等式バージョン)解説授業

(6)漸化式
【基本の漸化式】
①等差数列の漸化式
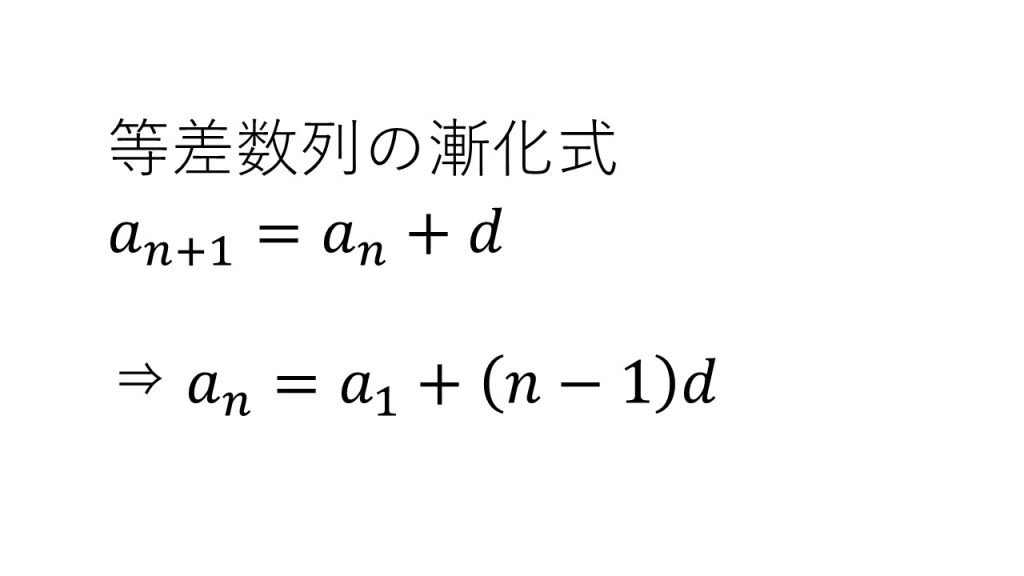
②等比数列の漸化式

【漸化式の基本パターン】
①特性方程式を利用して解く漸化式

②n乗の項を含む漸化式
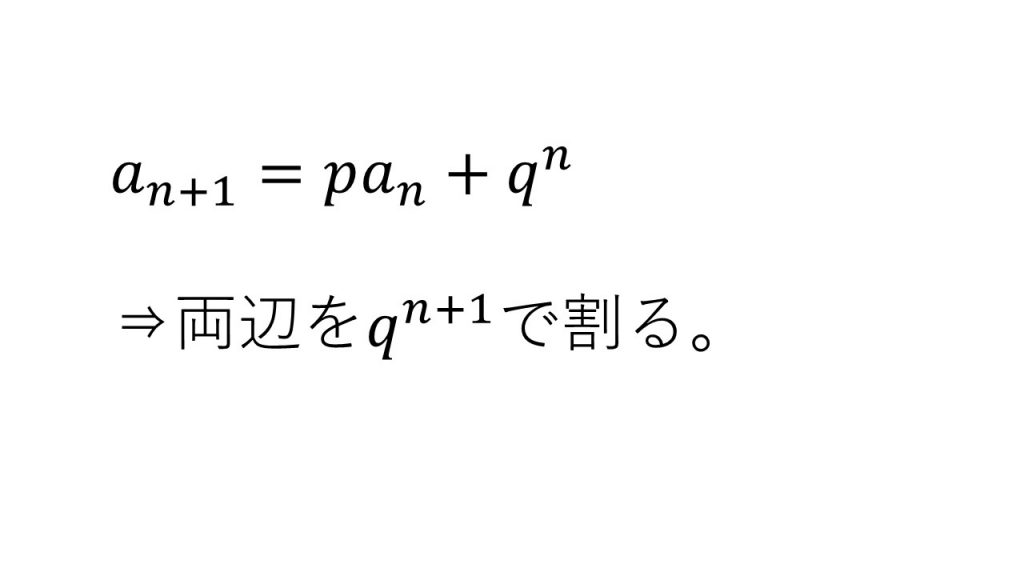
③分母と分子にanを含む漸化式
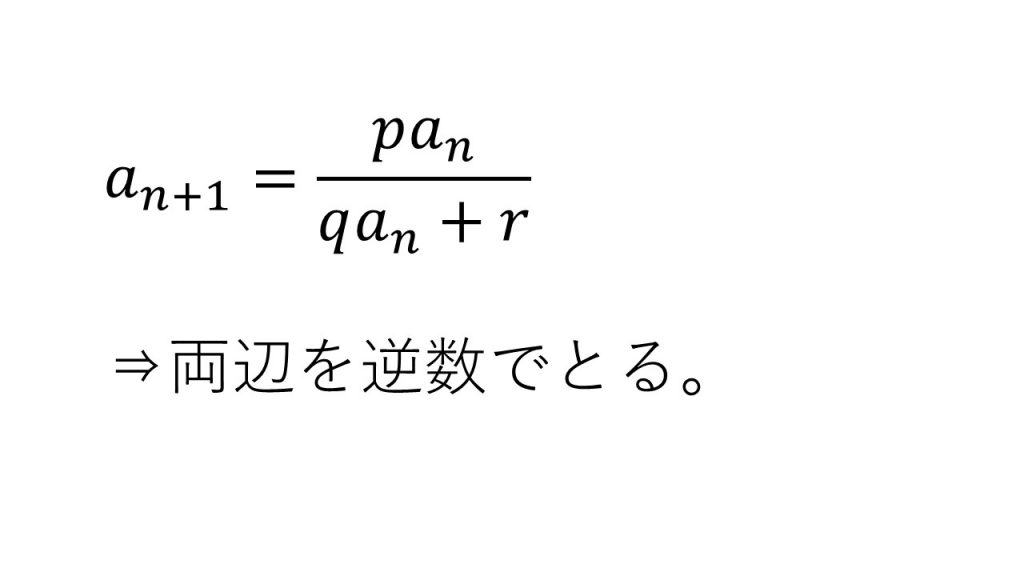
④anan+1を含む漸化式
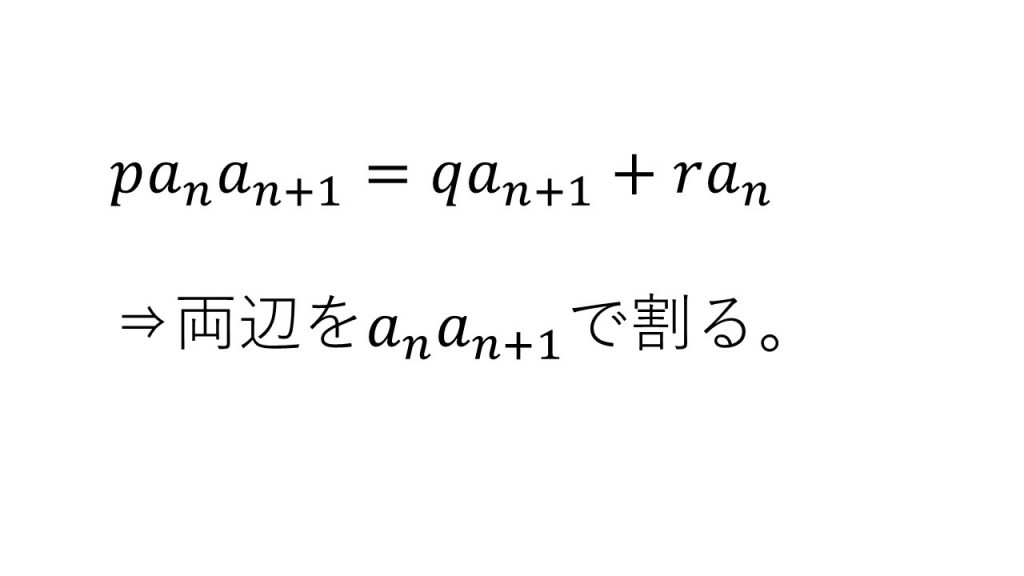
⑤anにルートや指数がついている漸化式

⑥和の式が与えられている漸化式

⑦階差数列の公式を利用して解く漸化式

⑧an+1=pan+f(n)
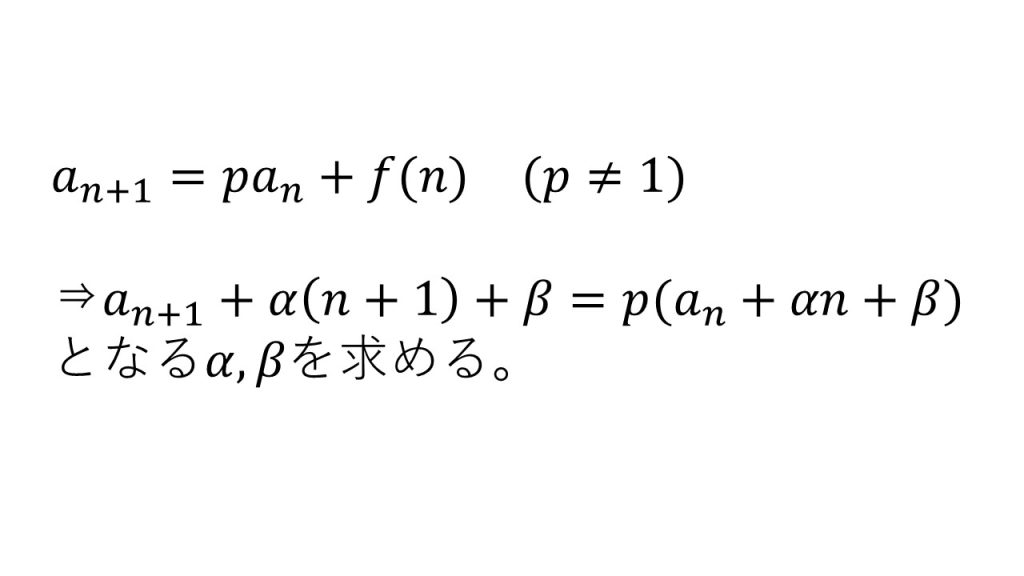
【漸化式の応用パターン】
①隣接3項間漸化式

②一般項を予想して数学的帰納法で証明するパターン

→一般項を予想して数学的帰納法で証明するパターンの漸化式解説授業
