電離平衡で考える塩の加水分解（「塩の加水分解は存在しない」と言える理由、計算の進め方、水のイオン積についても解説しています）【化学計算の王道】

（１）解説授業動画

☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル

（２）解説授業の原稿

電離平衡で考える塩の加水分解

今回は電離平衡という観点で塩の加水分解を考えてみようと思います。

まずは結論から言うと、電離平衡という観点で考えると、塩の加水分解という現象は存在しないということが言えます。もう少しちゃんと言うと、電離平衡を考えると、塩の加水分解という名前の固有の現象は存在しないということになります。

電離平衡の基本（弱酸・弱塩基の電離度とpHを求めます。近似についても解説しています）

「中和と塩」の単元における塩の加水分解

ではなぜ、このように言うことができるのか考えていきたいのですが、その前にまず「中和と塩」の単元で、塩の加水分解をどのように学んだか確認します。

塩の加水分解という現象は、「中和と塩」の単元で最初に学習します。どのように学習したかを簡単に確認すると、例えば酢酸ナトリウムという塩が含まれている水溶液があったとしたら、酢酸ナトリウムは塩なので、

CH₃COONa → CH₃COO^－＋Na⁺

と、ほぼ100%電離します。例外を除いて、塩は水溶液中でほぼ100%電離するのでした。そして、電離した2つのイオンのうち、ナトリウムイオンは強塩基のイオンなのでこれ以上何かをすることはありません。

しかし、酢酸イオンは弱酸のイオンです。弱酸は視点を変えてみると、元に戻ろうとする力が強いという性質を持っているので、水から水素イオンを奪って、

CH₃COO^－＋H₂O ⇆ CH₃COOH＋OH^－

のように、酢酸に戻ろうとします。そして水素イオンを奪われた水は、水酸化物イオンとなり、水酸化物イオンがあるのでこの水溶液は塩基性となります。

この反応のことを「塩の加水分解」と言い、「中和と塩」の単元では、塩を含む水溶液の液性を考えるために塩の加水分解を学習しました。

塩の加水分解と弱酸遊離の原理（弱酸の性質によって起きる現象）

水のイオン積

今回は、電離平衡という観点でこの現象を考えてみようと思います。ただその前に水のイオン積というものを確認します。

先ほど酢酸イオンは、水から水素イオンを奪って酢酸に戻ろうとすると言いましたが、水はわずかではありますが、

H₂O ⇆ H⁺＋OH^－

のように水素イオンと水酸化物イオンに電離しています。そのわずかな水素イオンを酢酸イオンが捕まえているのです。

このように水はごくわずかではありますが、常に水素イオンと水酸化物イオンに電離しています。そして、この水から電離した水素イオンのモル濃度[H^＋]と水酸化物イオンのモル濃度[OH^－]の積[H^＋][OH^－]のことを水のイオン積といい、よくK_wと書かれます。そして、

H₂O ⇆ H⁺＋OH^ー

は平衡状態を作っているので、温度を変えない限り水のイオン積K_wは一定となります。特に25℃のときは水のイオン積は1.0×10^－14(mol/L)²となります。25℃のときの水のイオン積の値は覚えておきましょう。

また、モル濃度の積なので(mol/L)×(mol/L)で、水のイオン積の単位は(mol/L)²となります。この水のイオン積は塩の加水分解を電離平衡で考えるときに重要となります。

水のイオン積が一定になる理由

ちなみに水のイオン積が一定となることをもう少し詳しく説明すると、H₂O ⇆ H⁺＋OH^－の平衡における平衡定数をKとすると平衡定数の定義より

K=[H^＋][OH^－]/[H₂O]

となります。そして、この式の両辺を水のモル濃度でかけて分母をはらうと

K[H₂O]=[H^＋][OH^－]

のようになります。ここで水の電離はごくわずかしか起こっておらず、電離せずに残っている水が多量に存在するということを考えると、この式の左辺はまとめて定数扱いすることができます。なぜなら水の量は、電離している水素イオンや水酸化物イオンの量に比べてはるかに多いため、この電離による量の変化はないものとして考えることができ、水の量は一定であるとみなすことができるからです。

よって、この左辺(K[H₂O])を1つの定数としてK_wとおけば、水のイオン積の式

K_w=[H⁺][OH^－]

ができます。そして平衡定数は温度を変えない限り一定なので、このK_wも温度を変えない限り一定となります。

化学平衡の基本（化学平衡とは何か、可逆反応・不可逆反応、グラフの読み取り、平衡定数の定義、化学平衡の法則・質量作用の法則）

このように水溶液中で水は多量に存在するので、その量がほとんど変化せず一定であるとみなしてよいという考え方はこの後でも重要になってきます。

例題：酢酸ナトリウム水溶液の加水分解

それでは問題を解きながら、電離平衡の観点で塩の加水分解を考えてみます。

0.10mol/LのCH₃COONa水溶液の[OH^－]を求めよ。ただし、酢酸イオンの電離定数K_a=1.8×10^－5mol/L、水のイオン積K_w=1.0×10^－14(mol/L)²とする。また、有効数字は2桁で答えます。

まずは先ほども確認した通り、酢酸ナトリウムは塩なので、

CH₃COONa → CH₃COO^－＋Na⁺

のように、酢酸イオンとナトリウムイオンに100%電離します。そして平衡前の酢酸イオンのモル濃度をCとし、平衡に達した後の水酸化物イオンのモル濃度つまり今回求める水酸化物イオン([OH^－])をxとします。

酢酸イオンのモル濃度であるCは0.10mol/Lのことです。なぜなら、酢酸ナトリウムと酢酸イオンの係数の比は1:1なので酢酸ナトリウムの濃度が0.10mol/Lであれば、酢酸イオンの濃度も0.10mol/Lとなるからです。そのためCではなく、0.10としても問題ありません。ただ、今回はまず一般的に式を作ってから、あとで数値を代入しようと思うので、とりあえず文字で置いて式を作っていきます。

①K_hをCとxで表す。

酢酸ナトリウムから電離した酢酸イオンは、

CH₃COO^－＋H₂O ⇆ CH₃COOH＋OH^－

のように加水分解を起こします。この塩の加水分解は平衡状態を作るので、反応前、変化量、反応後の表を作ります。

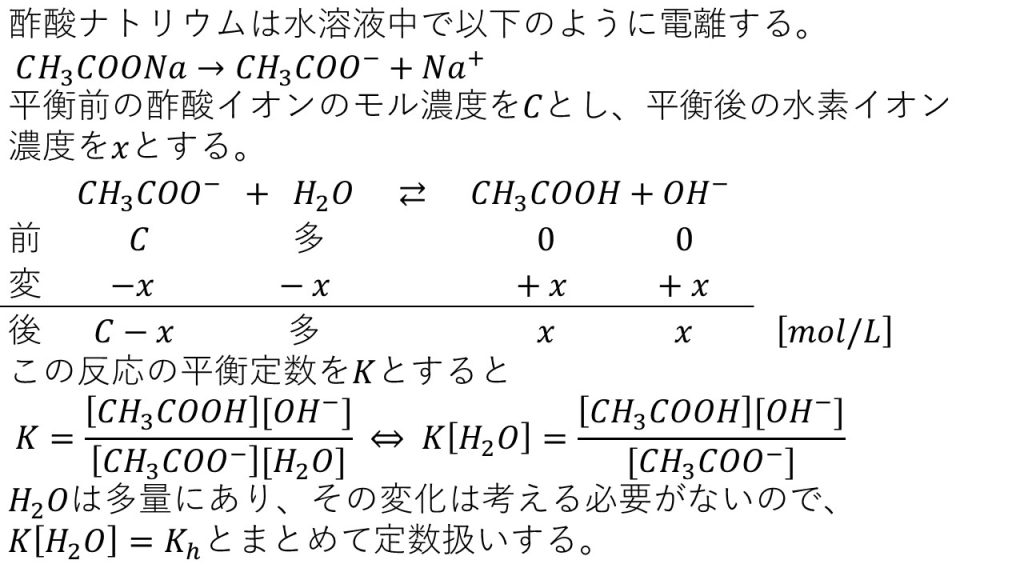
まず反応前は、酢酸イオンのモル濃度はCで、水は水溶液なので多量に存在します。そして、酢酸と水酸化物イオンは反応前なので0です。

次に変化量ですが、平衡に達した後の水酸化物イオン濃度をxとしているので、水酸化物イオンの変化量は+xとなります。よって、化学反応式の係数の比は1:1:1なので、左辺は－xで右辺は+xとなります。

したがって、平衡に達した後のモル濃度は反応前の変化量を足して、酢酸イオンはC－xとなり、水は多量に存在するものからほんの少しだけ減少するので変化していないとみなすことができ、反応前後で一定であると考えます。そして酢酸のモル濃度はxで、水酸化物イオンのモル濃度もxです。

これで平衡に達した後のモル濃度が分かったので、平衡の計算の基本通り、平衡定数の式を作ります。まずは定義にしたがって、

K=[CH₃COOH][OH^－]/ [CH₃COO^－][H₂O]

右辺のモル濃度/左辺のモル濃度とします。両辺を水のモル濃度でかけて、

K[H₂O]= [CH₃COOH][OH^ー]/[CH₃COO^ー]

となり、先ほどの解説した通り、水は一定であるとみなすことができるので左辺はまとめて定数扱いでき、左辺をK_hという定数で置き直すと、式は

K_h= [CH₃COOH][OH^－]/[CH₃COO^－]

のようになります。ちなみに、このK_hのことを加水分解定数と呼んだりもします。

次に、この式に平衡後のモル濃度を代入すると、x・x/C－xになります。

そして、ここから電離平衡の特殊な計算である近似ができます。なぜなら水の電離はごくわずかしか起きておらず、そのごくわずかの水素イオンを使って加水分解を起こしているので、xはCに比べて非常に小さいため、 C－xはCとみなすことができるのです。そのため、分母がC－x≒Cとなり、K_h=x²/Cとなります。

電離平衡の基本（弱酸・弱塩基の電離度とpHを求めます。近似についても解説しています）

②K_hをK_aとK_wで表す。

これでK_hをCとxで表すことができたのですが、ここまでではこの問題の答案の半分しかできていません。なぜならK_hの値が分かっていないので、方程式を立ててxの値を求めることができないからです。

そのため、次はK_hの値をK_aとK_wを使って求めていきます。

それではK_hの値を求めていきます。酢酸はCH₃COOH ⇆ CH₃COO^－＋H⁺のように電離するので、電離定数K_aは[CH₃COO^－][H⁺]/[CH3COOH]となります。そして水のイオン積は、K_w=[H⁺][OH⁺]となります。

これらを踏まえて加水分解定数K_h= [CH₃COOH][OH^－]/[CH₃COO^－]を式変形していきます。

この式から次の式に進めるために、少し特殊な式変形を行います。それは分母と分子に水素イオン濃度[H⁺]をかけます。分母と分子に同じものをかけているので、イコールは成り立ちます。

そして、分母の[CH₃COO^－][H⁺]と分子の[CH₃COOH]を見ると、K_aの逆数になっています。さらに分子の[OH^－][H^＋]はK_wとなっています。したがって、

K_h= K_w/K_a

となるのです。この部分の式変形に関しては、後ほど補足します。とりあえず計算を進めて答えを求めていきます。

③工夫しながら方程式を解く。

K_hはK_w/K_aとなったので、先ほど求めたK_h=x²/Cと合わせると、

x²/C= K_w/K_a

となります。次にCとK_aとK_wの値を代入して、xについて解くとx=√1/1.8×10^－10となります。

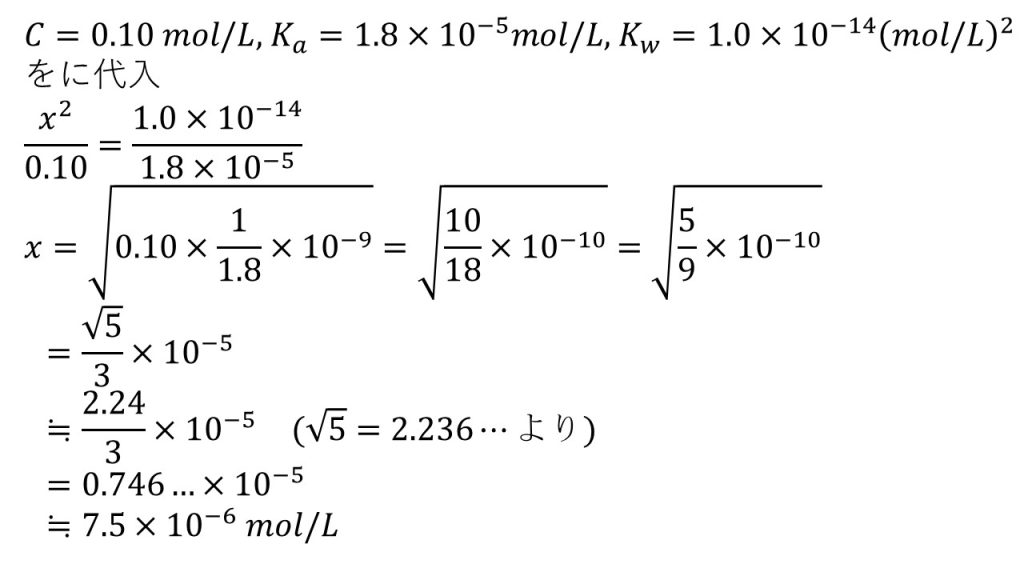
ここからはルートを外していく計算となります。ポイントはいかに2乗を作るか、あるいは、√2、√3、√5で表すかといったところです。

まずは1/1.8を10/18とします。そして2で約分すると5/9となるので、分母が3の2乗となりルートを外すことができ、√5/3×10⁻⁵になります。そして、√5=2.236…なので、√5=2.23あるいは2.24とし、割り算をして、有効数字が2桁になるように四捨五入して、答えは7.5×10⁻⁶mol/Lとなります。

これで弱酸の塩の水溶液の水酸化物イオン濃度を求めることができました。今回は問われていませんが、ここから水素イオン濃度を求めたり、pHを求めることもできます。

pHの計算（対数を使った計算、pOHとの関係、水のイオン積Kwについても解説しています）

K_h=K_w/K_aへの式変形の補足

さて、ここでK_h=[CH₃COO^－][H^＋]/[CH3COOH]からK_h=[CH₃COOH][OH^－][H⁺]/[CH₃COO^－][H⁺]への式変形の補足説明をします。

分母と分子に同じものをかけているので、数学的には問題ないことはわかると思いますが、それでもやはり、何もないところから水素イオンのモル濃度をかけていいのかと思うことでしょう。しかし、この水素イオンは実は何もないところからきたわけではなく、ちゃんとその出所があります。

それはどこかというと、この水素イオンは水の電離によって生じた水素イオンなのです。

今回求めた水酸化物イオン濃度を見てもらったら分かるとおり、塩の加水分解によって生じる水酸化物イオンの量はごくわずかです。7.5×10^－6ということは、0.0000075といったごくごくわずかな世界の話をしているので、そのような状況では、水のごくわずかな電離も無視することができないのです。

例えばpHが8以上あるいは6以下の世界では、水の電離は無視してもよいのですが、pHが7前後の世界の話では、水の電離すらも無視できないレベルの小さな世界の話をしているのです。そのため、式の中に水の電離の要素が入ってくるのです。