☆問題のみはこちら→積分(数学Ⅲ)計算全パターン(指数・対数)(問題)
①
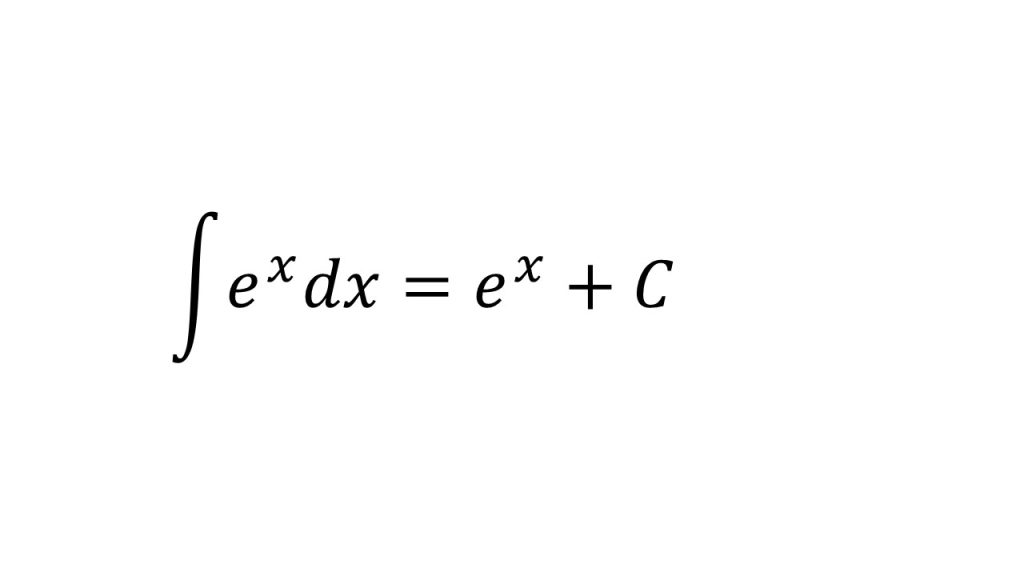
- 公式を利用しよう→積分法(数学Ⅲ)公式
②

- 公式を利用しよう→積分法(数学Ⅲ)公式
- 「積分は微分の逆である」ということを意識すれば、これがなぜ成り立つかが理解できる→「積分は微分の逆である」ということを意識して積分の公式を理解しよう!
③
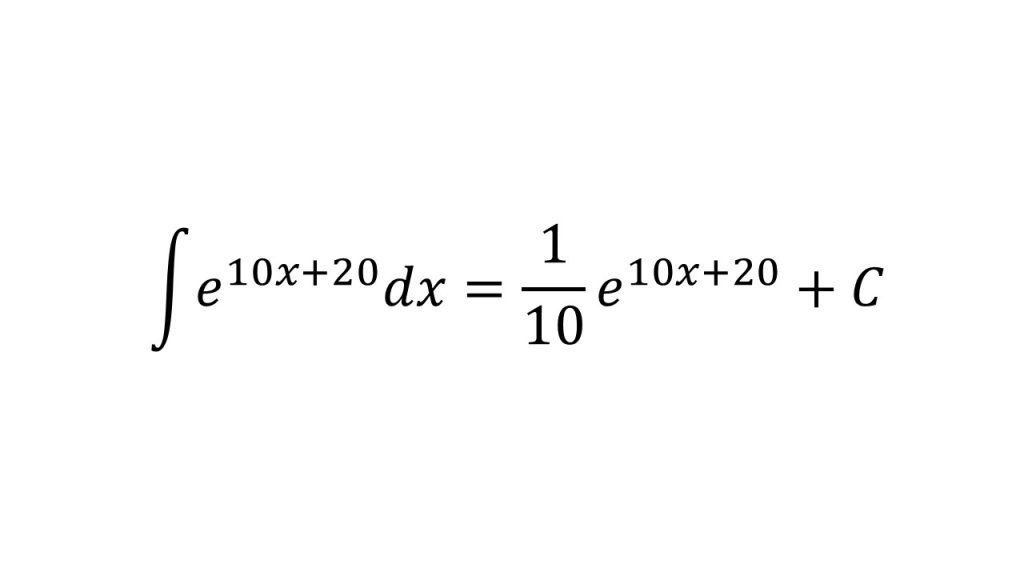
- e10x+20が合成関数であることに注意。合成関数の積分についてはこちら→合成関数の積分
④
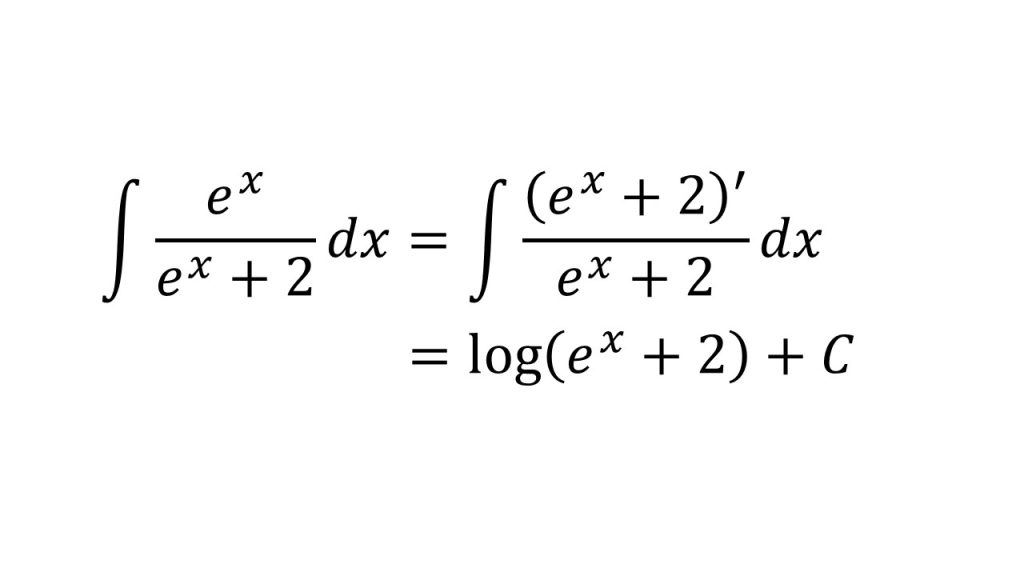
- f'(x)/f(x)の形にするパターン。なぜこれが成り立つか分からなければ、logf(x)を微分してみるとよい(対数関数の微分+合成関数の微分)。
⑤
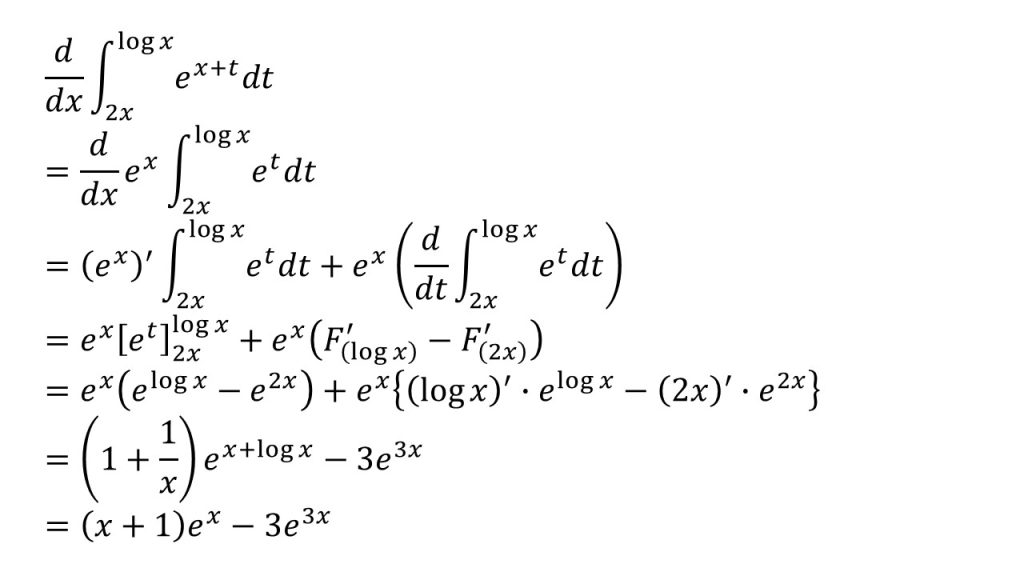
- 定積分で表された関数の微分をしている→積分法の応用(数学Ⅲ)公式
- 簡単にいうと、「積分した後、微分すれば元に戻る」ということ。
- ただし、積分区間にxを含む場合、合成関数の微分を使うのを忘れないようにしないといけない。F(logx), F(2x)は合成関数のため、F'(logx)-F'(2x)=f(logx)-f(2x)としてはいけない。
- 2行目から3行目への式変形は積の微分を用いている→微分法(数学Ⅲ)公式
⑥
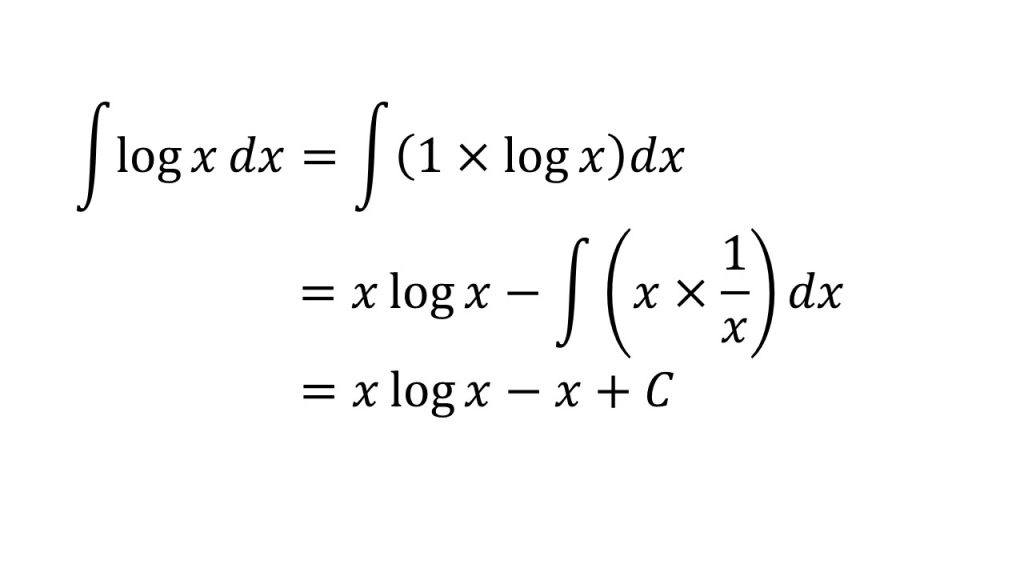
- 部分積分法を利用するために、logxを1×logxと考える。
- logxは積分がやりにくく、微分は分かりやすいので、公式のf(x)にする。(1をg(x)とする)
⑦
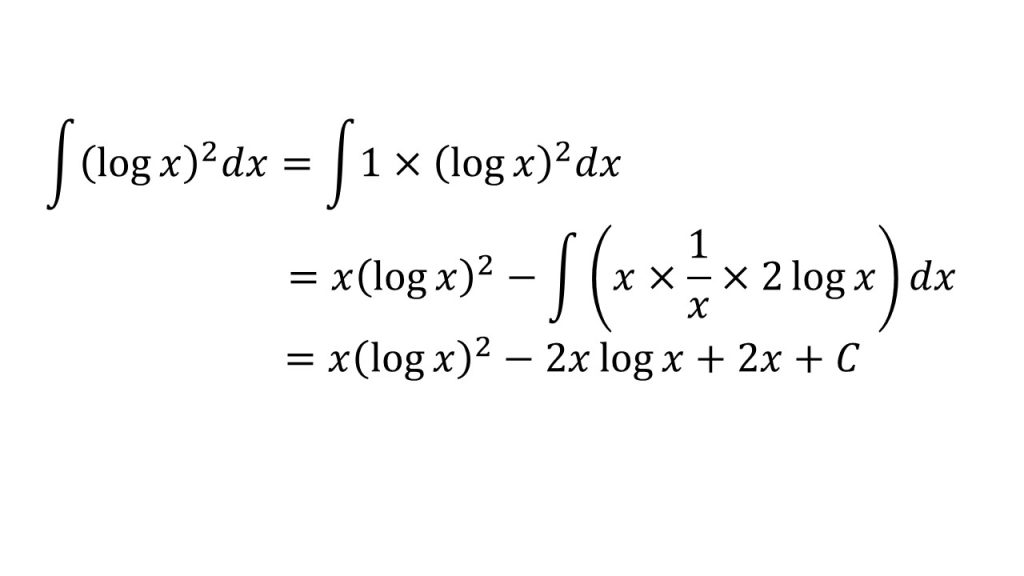
- 部分積分法を利用するために、(logx)2を1×(logx)2と考える。
- (logx)2は積分がよく分からず、微分は分かりやすいので、公式のf(x)にする。(1をg(x)とする。)
- (logx)2の微分は合成関数の微分→微分法(数学Ⅲ)公式
⑧
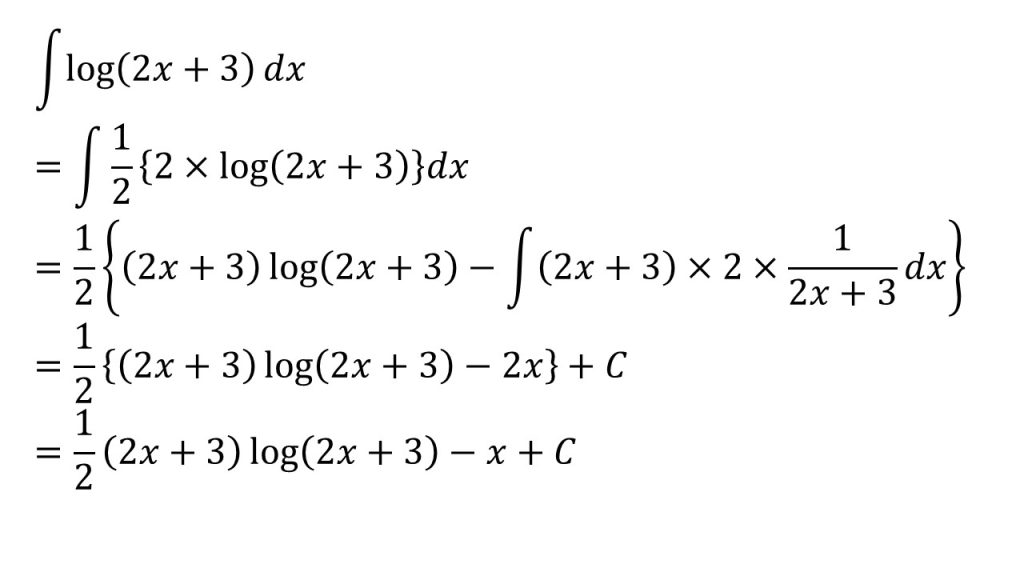
- 部分積分法を利用するために、log(2x+3)を2×log(2x+3)とする。つじつまを合わせるために1/2をかけるのを忘れないように。
- log(2x+3)は積分がよく分からず、微分は分かりやすいので、公式のf(x)にする。(2をg(x)とする。)
- 2x+3は2の原始関数の1つなので、2を不定積分したときは、2x+3としてよい。
- log(2x+3)の微分は合成関数の微分→微分法(数学Ⅲ)公式
☆問題のみはこちら→積分(数学Ⅲ)計算全パターン(指数・対数)(問題)
【式の種類別演習問題一覧】
【パターン別演習問題一覧】
~参考~
☆積分計算(数学Ⅲ)をマスターしよう(解説・授業・公式・演習問題一覧)
☆積分(数学Ⅲ)の計算公式の証明はこちら→「積分は微分の逆である」ということを意識して積分の公式を理解しよう!
☆微分計算(数学Ⅲ)をマスターしよう(解説・授業・公式・演習問題一覧)
