合成関数の積分（問題と答え）【積分計算（数学Ⅲ）をマスターしよう】

☆問題のみはこちら→合成関数の積分（問題）

☆積分（数学Ⅲ）の計算公式一覧

---

【公式】

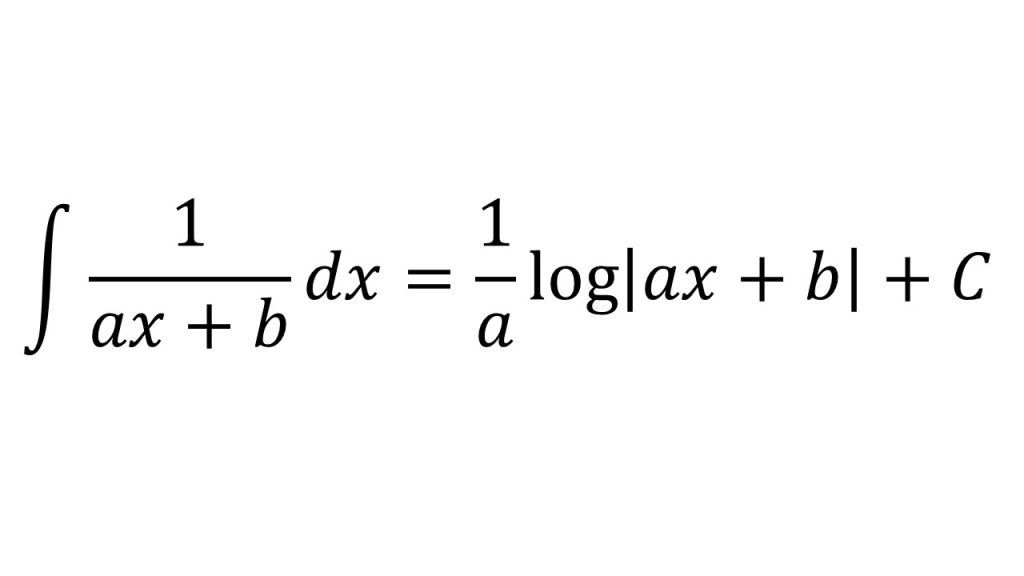
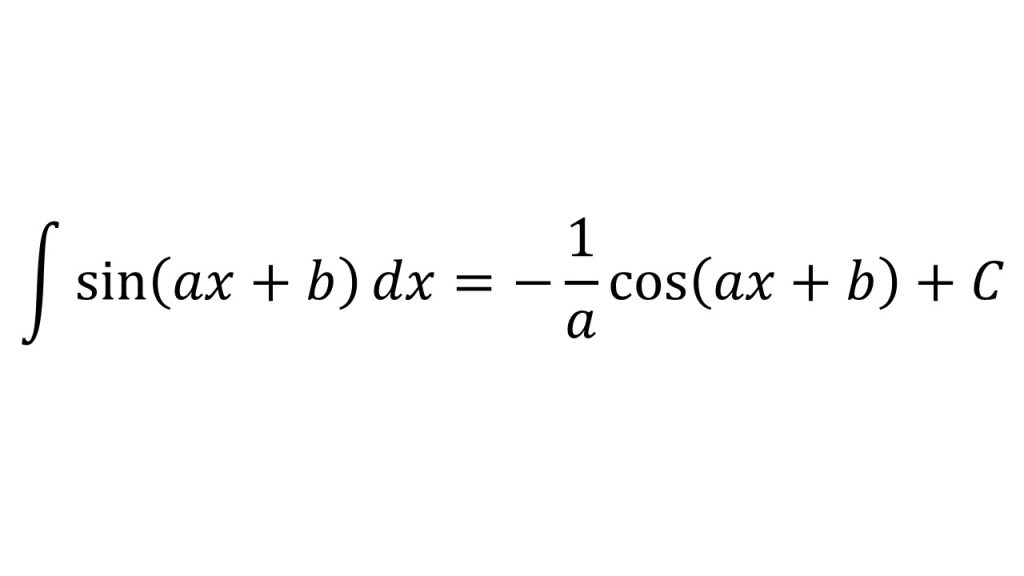
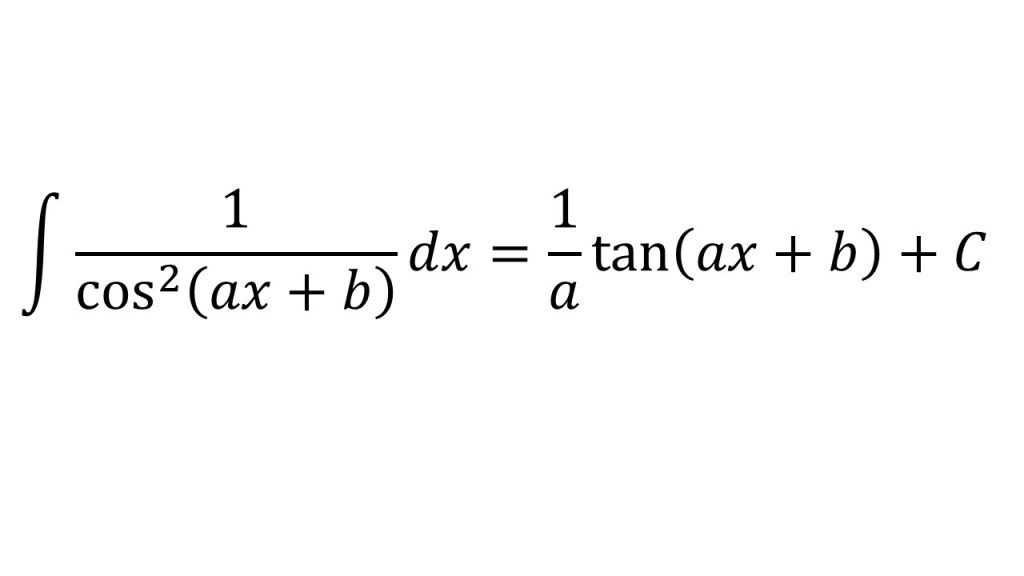
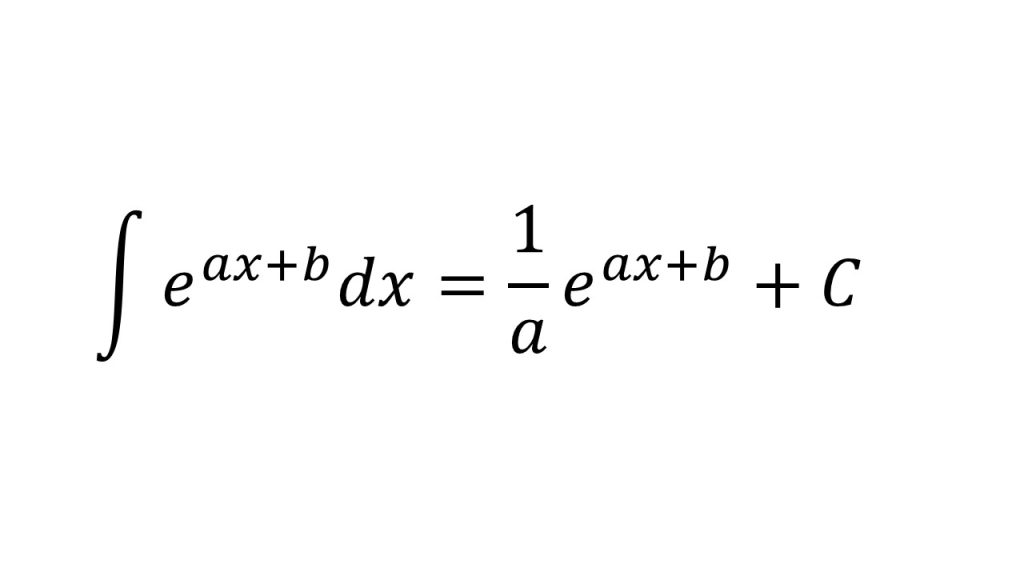
【ポイント】

計算の手順としては、
①全体を積分（f(g(x))のf(u)をuで積分）した後、
②中身の微分（f(g(x))のg(x)をxで微分）の逆数をかける。

右辺を微分してみて確かめてみるとよい。参考：「積分は微分の逆である」ということを意識して積分の公式を理解しよう！

【例題】

①

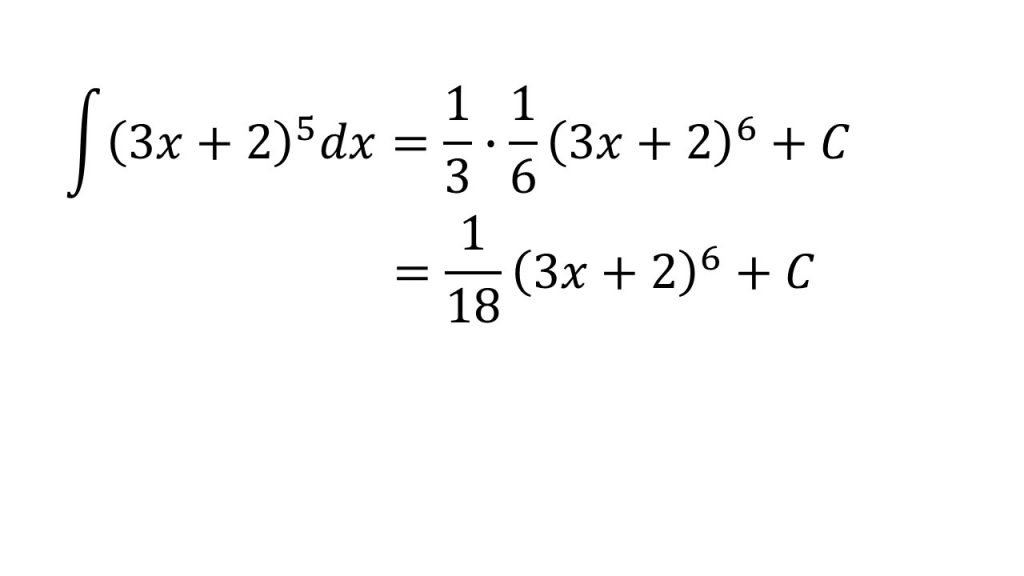
②

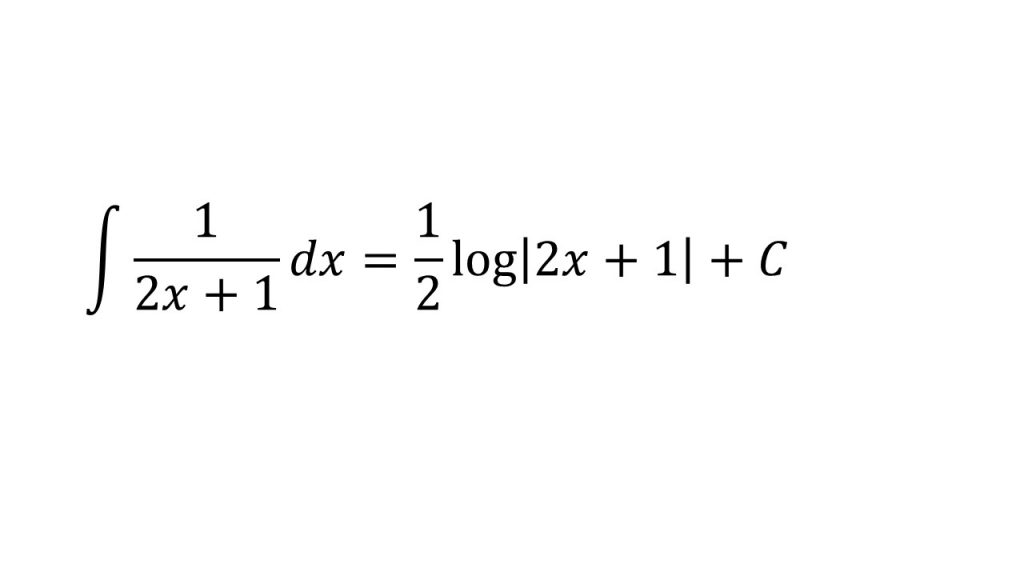
③

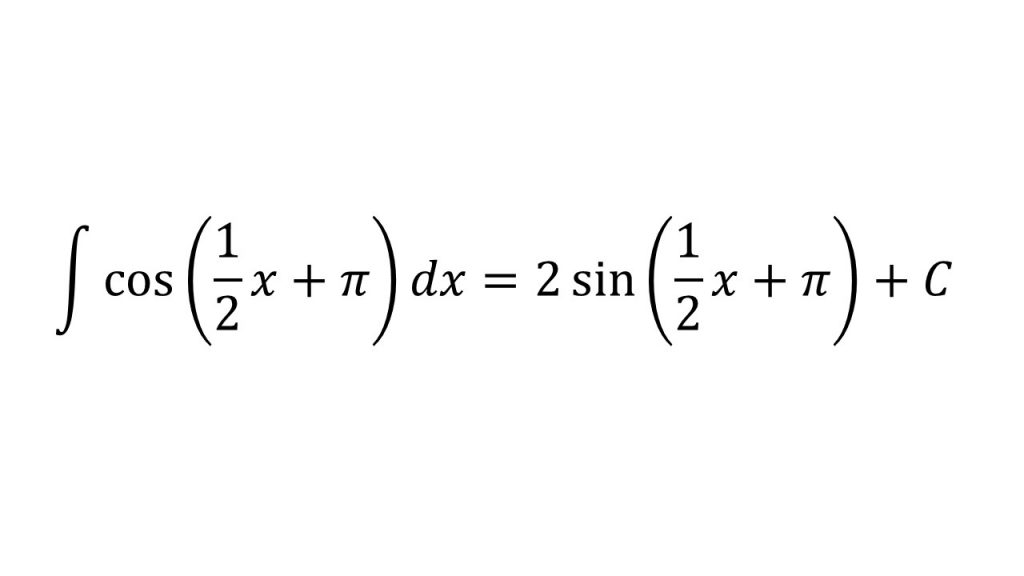
④

---

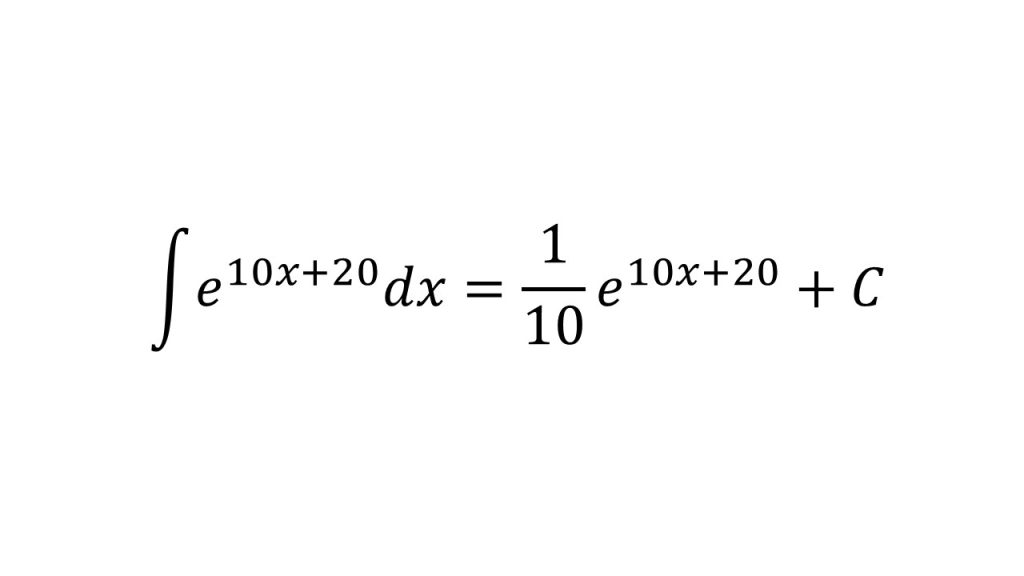
☆問題のみはこちら→合成関数の積分（問題）

☆積分（数学Ⅲ）の計算公式一覧

---

【式の種類別演習問題一覧】

①積分（数学Ⅲ）計算全パターン（整式）

②積分（数学Ⅲ）計算全パターン（三角関数）

③積分（数学Ⅲ）計算全パターン（指数・対数）

④積分（数学Ⅲ）計算全パターン（異なる関数の積）

【パターン別演習問題一覧】

①合成関数の積分

②置換積分法

③分数式の積分

④部分積分法

---

～参考～

☆積分計算（数学Ⅲ）をマスターしよう（解説・授業・公式・演習問題一覧）

☆積分（数学Ⅲ）の計算公式一覧

☆積分（数学Ⅲ）の計算公式の証明はこちら→「積分は微分の逆である」ということを意識して積分の公式を理解しよう！

☆微分法（数学Ⅲ）の計算公式一覧

☆微分計算（数学Ⅲ）をマスターしよう（解説・授業・公式・演習問題一覧）

☆数学Ⅲ公式一覧

☆数学Ⅲの解説・授業・公式・演習問題一覧

☆数学の解説動画・授業動画一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学公式一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の解説・授業・公式・演習問題一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学典型パターン一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の語呂合わせ

☆数学学習に必要な参考書・問題集