積分（数学Ⅲ）計算全パターン（異なる関数の積）（問題と答え）【積分計算（数学Ⅲ）をマスターしよう】

☆問題のみはこちら→積分（数学Ⅲ）計算全パターン（異なる関数の積）（問題）

☆積分（数学Ⅲ）の計算公式一覧

---

①

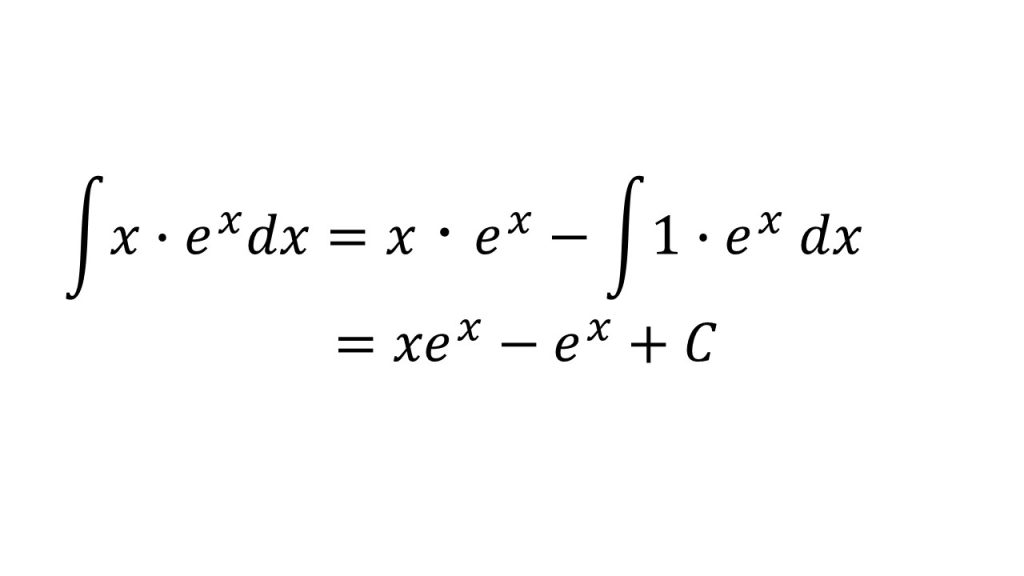
• 部分積分法を用いる。
• xをf(x)（微分すると簡単になるもの）、e^xをg(x)（微分してもあまり形が変わらないもの）とする。

②

• 部分積分法を用いる。
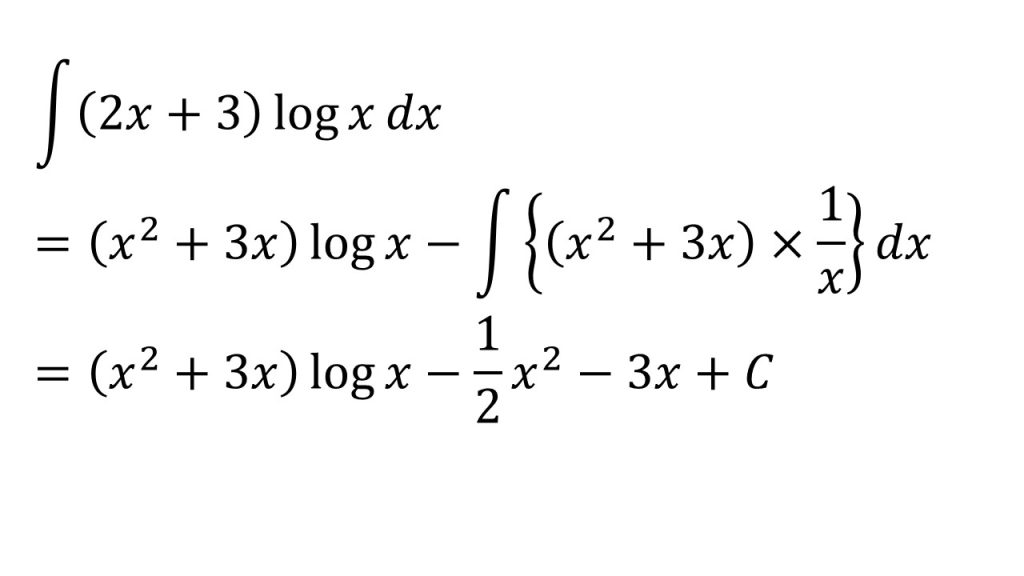
• logxは積分するのに部分積分法が必要になるので、logxは積分しなくてもよいf(x)に、積分が簡単な2x+3をg(x)とする。

③

• 部分積分法では上手くいかない。
• x³+1の微分が3x²であると気がつけば、置換すれば上手くいくと気がつくことができる→置換積分法

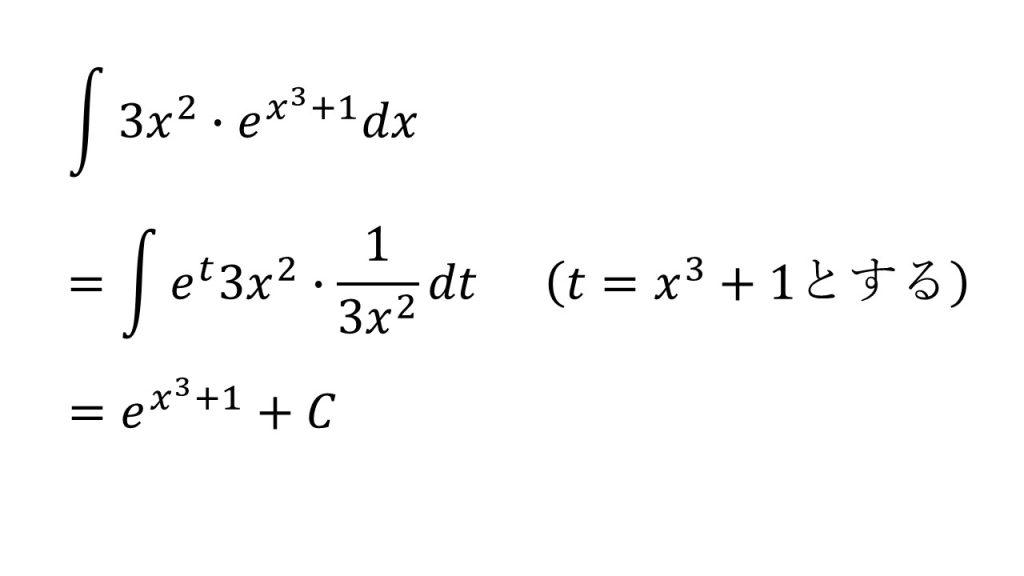
④

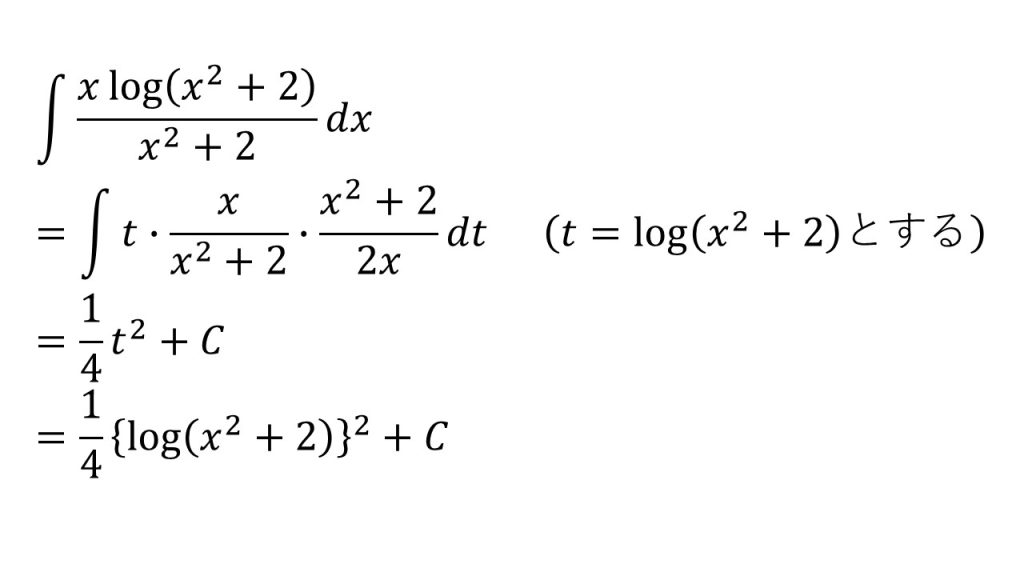
• t=x²+2としても上手くいかない。
• log(x²+2)の微分（合成関数の微分）が2x/(x²+2)であると気がつけば、t=log(x²+2)と置換すれば上手くいくと気がつくことができる→置換積分法

⑤

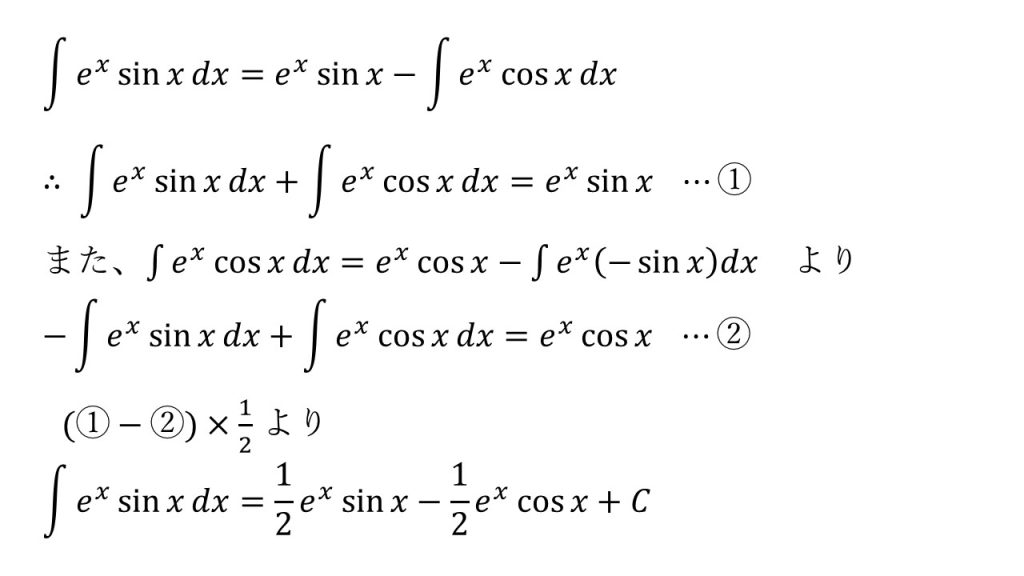
• 部分積分法を用いると、∫e^xsinxdxと∫e^xcosxdxという形が繰り返し現れることに気がつく（同形反復）。このような場合は、連立させると上手くいく。

⑥

• 積分区間が－aからaのときは計算を簡単にすることができる。偶関数の定積分と奇関数の定積分についてはこちら→積分法（数学Ⅲ）公式

⑦

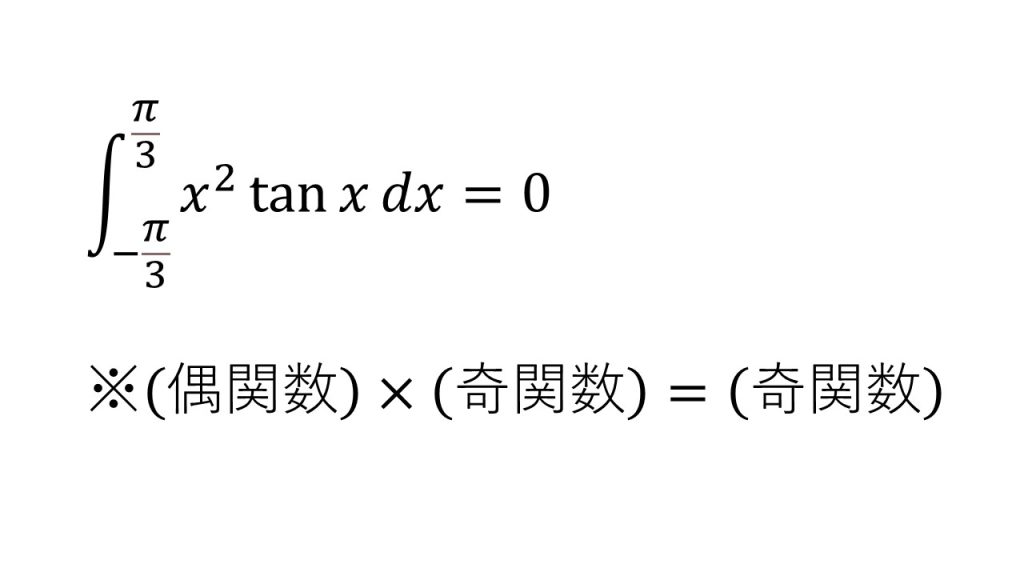
• 積分区間が－aからaのときは計算を簡単にすることができる。偶関数の定積分と奇関数の定積分についてはこちら→積分法（数学Ⅲ）公式
• x²は偶関数で、tanxは奇関数である。
• 偶関数×奇関数＝奇関数となる。

⑧

• 積分区間が－aからaのときは計算を簡単にすることができる。偶関数の定積分と奇関数の定積分についてはこちら→積分法（数学Ⅲ）公式
• sinxは奇関数で、3xも奇関数である。
• ∫{f(x)+g(x)}dx=∫f(x)dx+∫g(x)dx

⑨

• 積分区間が－aからaのときは計算を簡単にすることができる。偶関数の定積分と奇関数の定積分についてはこちら→積分法（数学Ⅲ）公式
• xは奇関数で、cosxは偶関数で、x²は偶関数である。
• 偶関数×奇関数＝奇関数となる。
• ∫{f(x)+g(x)}dx=∫f(x)dx+∫g(x)dx

---

☆問題のみはこちら→積分（数学Ⅲ）計算全パターン（異なる関数の積）（問題）

☆積分（数学Ⅲ）の計算公式一覧

---

【式の種類別演習問題一覧】

①積分（数学Ⅲ）計算全パターン（整式）

②積分（数学Ⅲ）計算全パターン（三角関数）

③積分（数学Ⅲ）計算全パターン（指数・対数）

④積分（数学Ⅲ）計算全パターン（異なる関数の積）

【パターン別演習問題一覧】

①合成関数の積分

②置換積分法

③分数式の積分

④部分積分法

---

～参考～

☆積分計算（数学Ⅲ）をマスターしよう（解説・授業・公式・演習問題一覧）

☆積分（数学Ⅲ）の計算公式一覧

☆積分（数学Ⅲ）の計算公式の証明はこちら→「積分は微分の逆である」ということを意識して積分の公式を理解しよう！

☆微分法（数学Ⅲ）の計算公式一覧

☆微分計算（数学Ⅲ）をマスターしよう（解説・授業・公式・演習問題一覧）

☆数学Ⅲ公式一覧

☆数学Ⅲの解説・授業・公式・演習問題一覧

☆数学の解説動画・授業動画一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学公式一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の解説・授業・公式・演習問題一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学典型パターン一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の語呂合わせ

☆数学学習に必要な参考書・問題集