(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
今回は、高次式の因数分解と高次方程式を解説します。
高次式とは、x3-3x2-6x+8のように3乗以上を含む式のことで、高次方程式とはx3-3x2-6x+8=0のように高次式を含む方程式のことです。
因数定理
このような高次式の因数分解や高次方程式を解くためには、因数定理を理解していないといけません。
因数定理とは、
「1次式x-aが整式P(x)の因数である ⇔ P(a)」
という定理のことです。
⇔は同値または必要十分条件であるということを表す記号です。
- 同値・必要十分条件とは、必要条件かつ十分条件であるということ。つまり「P⇔Q」は「PならばQが真」かつ「QならばPが真」であることを意味している。
つまり、「x-aがP(x)の因数であるならばP(a)=0」が成り立ち、かつ、その逆の「P(a)=0ならばx-aがP(x)の因数である」も成り立つということを表しています。
このように、因数定理は言葉で正確に理解しておきましょう。
たまに、因数定理の理解をあいまいにしたまま高次式の因数分解をしている人がいますが、それではなぜこのようにすれば解けるのかを理解することができず、応用させることができなくなってしまいます。
そのため、因数定理などの定理や公式は、正確に理解するようにしましょう。
例題1:高次式の因数分解
それでは実際に因数定理を使って、高次式の因数分解や高次方程式を解いてみましょう。
x3-3x2-6x+8を因数分解してみます。
①高次式をP(x)とおく
まず答案を書きやすくするために、因数分解をする高次式をP(x)と置きます。
P(x)=x3-3x2-6x+8
②P(a)=0となるaを探す
そして、ここから因数分解をしていくのですが、因数分解をするための因数を探さないといけません。
そこで因数定理を使います。つまり、P(a)=0ならばx-aがP(x)の因数であるので、P(a)=0となるようなaを見つけることができれば、P(x)の因数を1つ見つけることができるのです。
よって、今回のP(x)であるx3-3x2-6x+8のxに代入して0となる数を探します。
③因数定理よりx-aがP(x)の因数の1つとなる
今回はxに1を代入すると、
P(1)=13-3・12-6・1+8=0
となります。したがって因数定理より、P(1)=0となるのでP(x)はx-1を因数にもつことが分かります。
このように、この段階で因数定理を使っているということを意識することが重要です。
④P(x)をx-aで割る
そして、因数の1つを見つけたら、あとは割り算をします。
つまり、P(x)を、見つけた因数x-1で割り算します。すると必ず割り切れます。もし割り切れない場合は、探してきた数が間違っていたということになります。
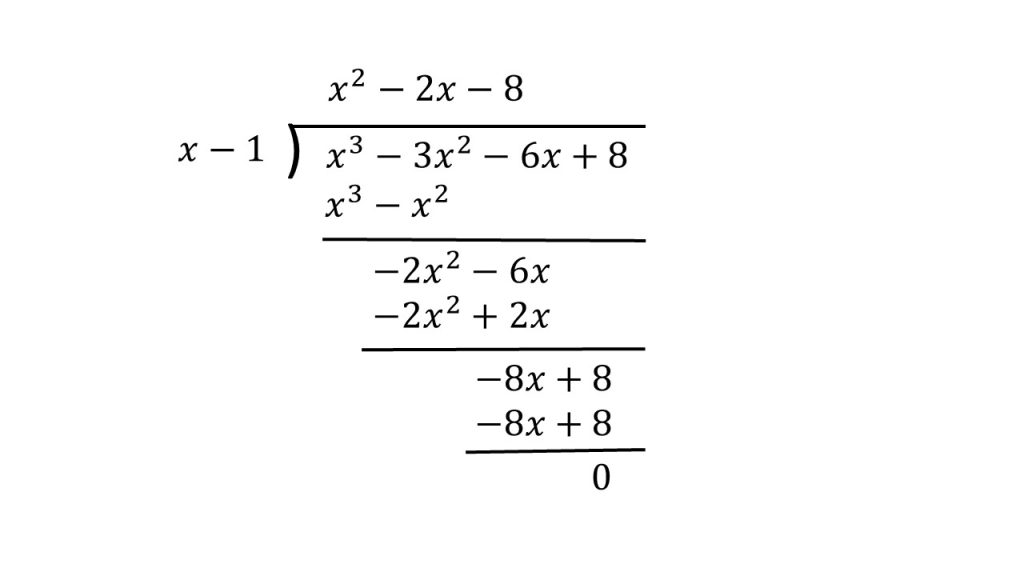
⑤P(x)=(x-a)(割り算の商)
このように割り算をすることで、P(x)は、因数定理で見つけてきた因数x-1と、割り算の商x2-2x-8で因数分解できることが分かります。
P(x)=(x-1)(x2-2x-8)
⑥まだ因数分解できる部分があれば、因数分解をして完成
そして最後に、2次式の部分x2-2x-8を因数分解して、P(x)の因数分解ができました。
P(x)=(x-1)(x2-2x-8)=(x-1)(x-4)(x+2)
このようにすれば、3次以上の高次式も因数分解することができるようになります。
【高次式の因数分解の手順】
- 高次式をP(x)とおく。
- P(a)=0となるaを探す。
- 因数定理よりx-aがP(x)の因数の1つとなる。
- P(x)をx-aで割る。
- P(x)=(x-a)(割り算の商)
- まだ因数分解できる部分があれば、因数分解をして完成。
ちなみに、今回P(1)=0としましたが、P(4)やP(-2)も0となるので、P(4)=0からx-4が因数になる、あるいは、P(-2)=0からx-2が因数になるとして因数分解することもできます。
因数定理の言い換え
また、今回P(x)はx-1で割り切れたように、「因数にもつ」ということは「割り切れる」ということでもあるので、因数定理は、
「整式P(x)は1次式x-aで割り切れる ⇔ P(a)」
と言い換えることもできるということも知っておきましょう。
例題2:高次方程式を解く
それでは次は、
3x3-2x2-6x+4=0
この方程式を解きます。この方程式は左辺の最高次数が3となっている3次方程式、つまり、高次方程式となっています。
高次方程式は基本的に左辺の高次式を因数分解して解きます。そのため、左辺の因数分解をするところまでは、先ほどの高次式の因数分解の流れと同じ流れになります。
実際にやってみましょう。
①左辺の高次式をP(x)とおく
まずは因数分解をする左辺をP(x)と置きます。
P(x)=3x3-2x2-6x+4
②P(a)=0となるaを探す
そして、因数定理を使って因数の1つを見つけるために、P(x)のxに代入して0となる数を探します。
ただ、ここで今回は少し悩んでしまいます。なぜなら、1や2あるいは-1や-2といった整数を代入してもP(x)は0にはならないからです。
先に答えを言うと、今回は2/3を代入することで0になります。
P(2/3)=3・8/27-2・4/9-6・2/3+4=0
では、このように分数を探してこないといけないときに、どのように見つければよいのでしょうか。
このように代入して0となる数を探すときは、

このように探すと見つけやすくなります。
今回で言えば、最高次の項の係数は3であり、定数項は4なので、±4/3、±2/3、±1/3あたりが候補になります。ここまで候補を絞れば、あとはいくつか代入してみて0となるものを見つけます。
- ちなみに、先ほどの高次式はx3-3x2-6x+8だったわけですが、こちらもこの探し方で、代入して0となる数の候補を挙げてみると、x3の係数が1なので、8の約数である±1、±2、±4、±8あたりが候補に挙がります。実際に答えは、1, -2, 4でした。
③因数定理よりx-aがP(x)の因数の1つとなる
このようにして、P(x)のxに2/3を代入すれば、P(x)は0となることが分かったので、因数定理よりP(x)はx-2/3を因数にもつことが分かります。
やはり、ここで因数定理を使っていることを意識しましょう。
④P(x)をx-aで割る
そして、因数の1つが分かったので、P(x)を因数で割り算します。

⑤P(x)=(x-a)(割り算の商)
すると必ず割り切れて、見つけた因数と割り算の商を使ってP(x)を因数分解することができます。
P(x)=(x-2/3)(3x2-6)
⑥まだ因数分解できる部分があれば、因数分解をして完成
そして、3をくくりだすと3(x2-2)となり、x2-2は(x+√2)(x-√2)と因数分解できます。
P(x)=(x-2/3)(3x2-6)=3(x-2/3)(x2-2)=3(x-2/3)(x+√2)(x-√2)
⑦方程式を解く
したがって、問題の方程式の解は、
x=2/3, ±√2
となります。
今回x2-2が因数分解できたので因数分解しましたが、2次式が因数分解できないときは、2次方程式の解の公式を使うことで解くことができます。
いかがだったでしょうか。高次式の因数分解や高次方程式の解き方が理解できたでしょうか。
これらの問題で特に重要なのは、因数定理を正しく理解し、因数定理を使っていると意識することです。また、高次式に代入して0となる数の見つけ方も知っておきましょう。
(3)解説授業の内容を復習しよう
(4)複素数と方程式(数学Ⅱ)の解説一覧
②解と係数の関係の証明(三次方程式の解と係数の関係も解説しています)
③高次式の因数分解・高次方程式の解法の解説(因数定理を正確に理解しよう!)
④根号や虚数単位iを含む式を代入して式の値を求める問題の解法(次数下げ)
⑤1の3乗根ω(オメガ)とは何か(ωの意味と使い方についての解説)
