置換積分法（問題と答え）【積分計算（数学Ⅲ）をマスターしよう】

【使いどころ】

1. g(x)・f(g(x))→g(x)=tとおく
2. g'(x)・f(g(x))→g(x)=tとおく
3. dxをdtに置き換えたときに、xが消去されるとき
4. √〇－x²が含まれるとき
5. 分母がx²+〇のとき
6. sinxを含む式の積分で上手くいかないとき→x=π/2－θと置換して、cosθに変換する

【例題】

☆問題のみはこちら→置換積分法（問題）

☆積分（数学Ⅲ）の計算公式一覧

---

①

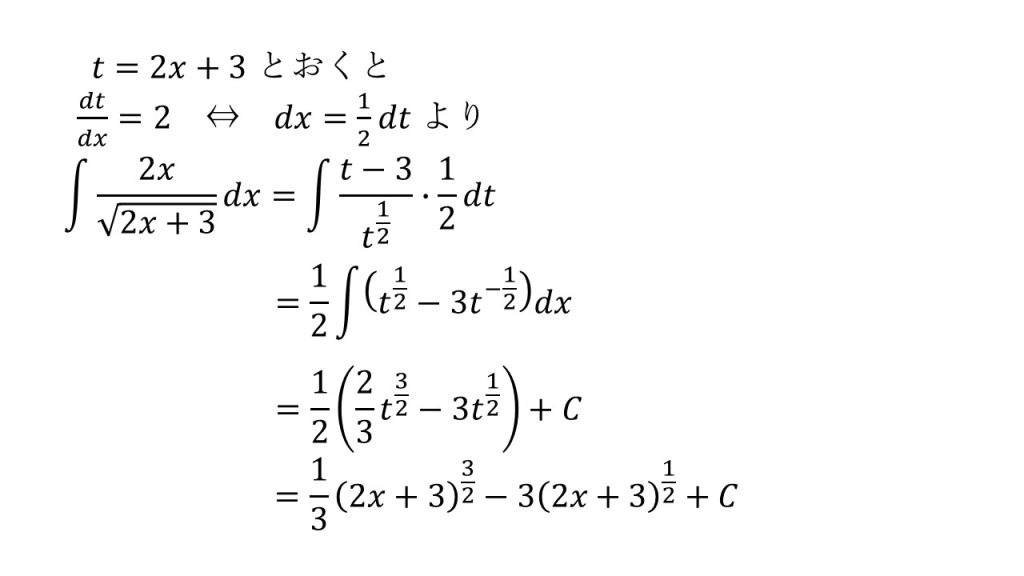
※t=2x+3とすることで分子の2xもtで表すことができる（xを消去することができる）。

①の別解

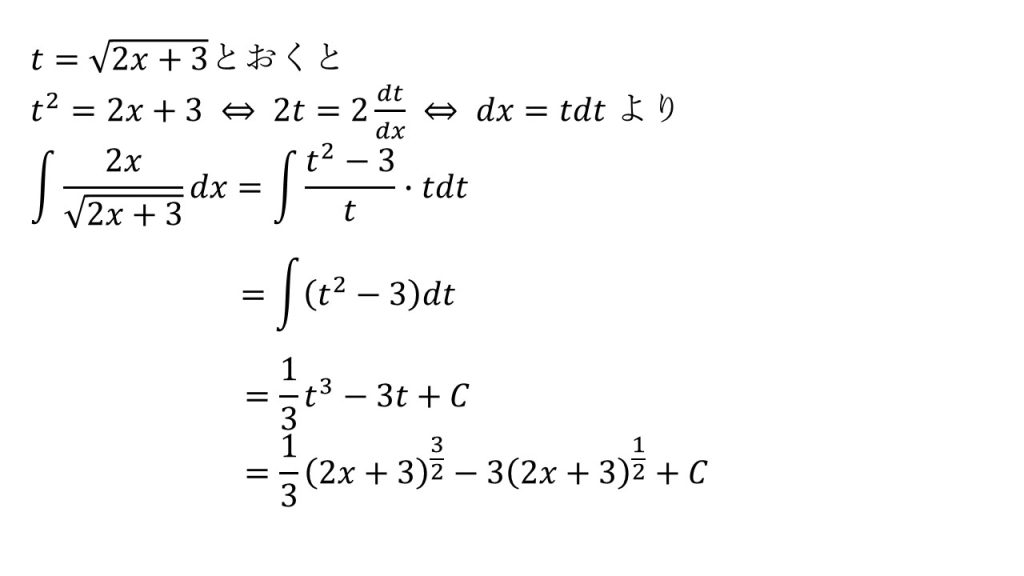
※置換積分法を使わない別解もある。詳しくはこちら→積分（数学Ⅲ）計算全パターン（整式）

②

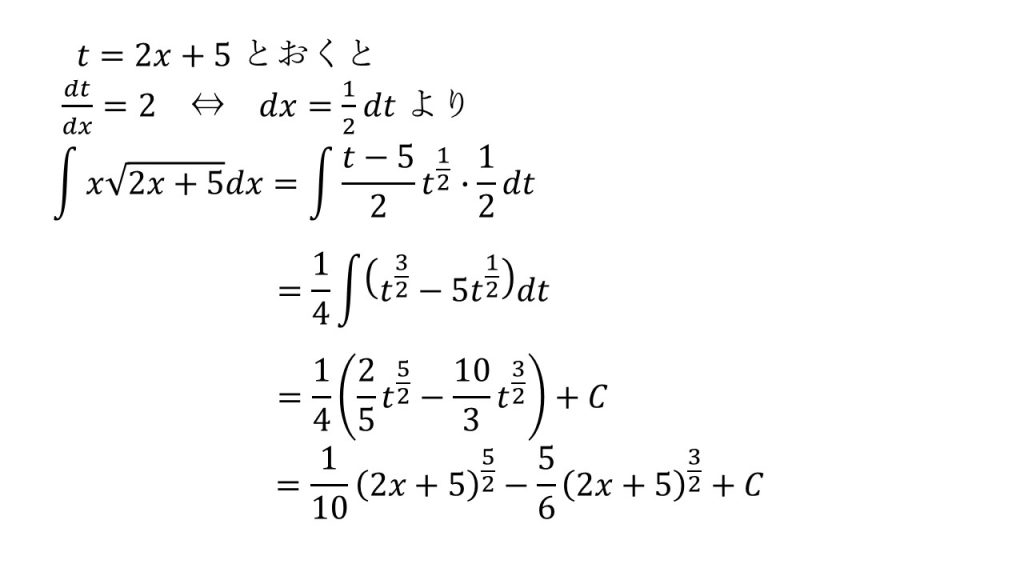
※t=2x+5とすることで係数のxもtで表すことができる（xを消去することができる）。

②の別解

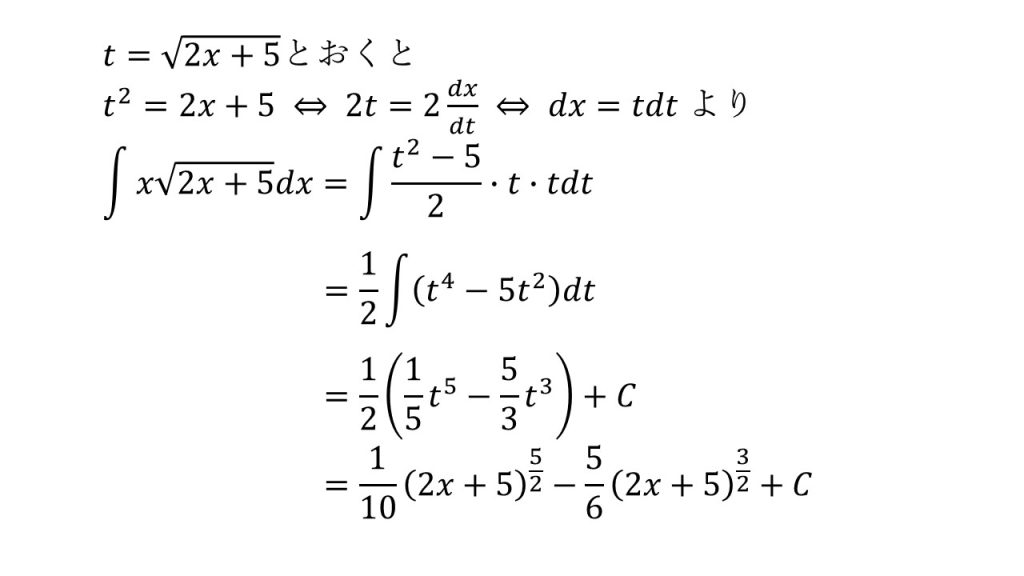
※置換積分法を使わない別解もある。詳しくはこちら→積分（数学Ⅲ）計算全パターン（整式）

③

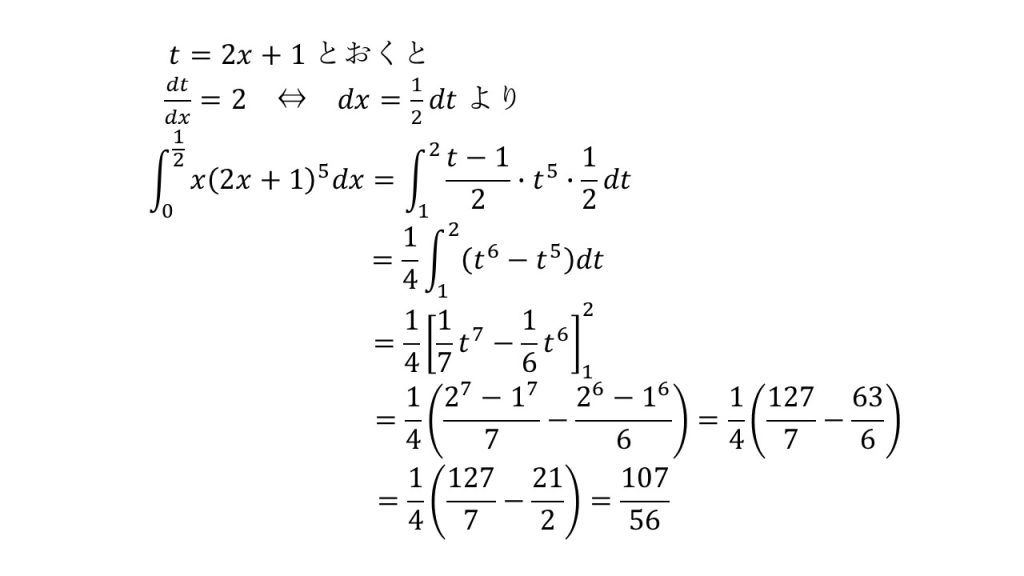
※t=2x+1とすることで係数のxもtで表すことができる（xを消去することができる）。
※置換積分法を使わない別解もある。詳しくはこちら→積分（数学Ⅲ）計算全パターン（整式）

④

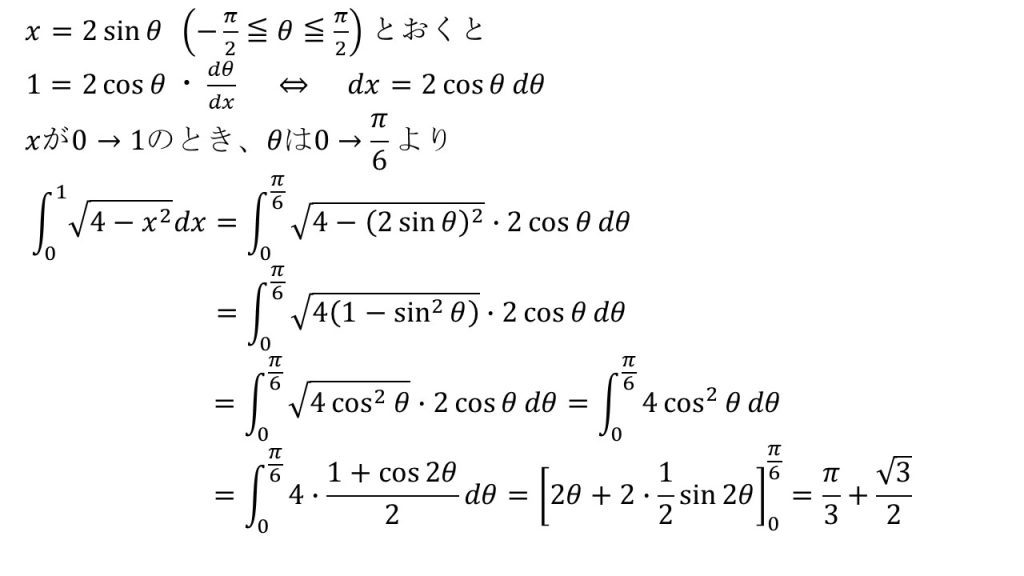
※√〇－x²のときは、x=2sinθと置換すると上手くいく。これは特殊な置換なので覚えておこう！

⑤

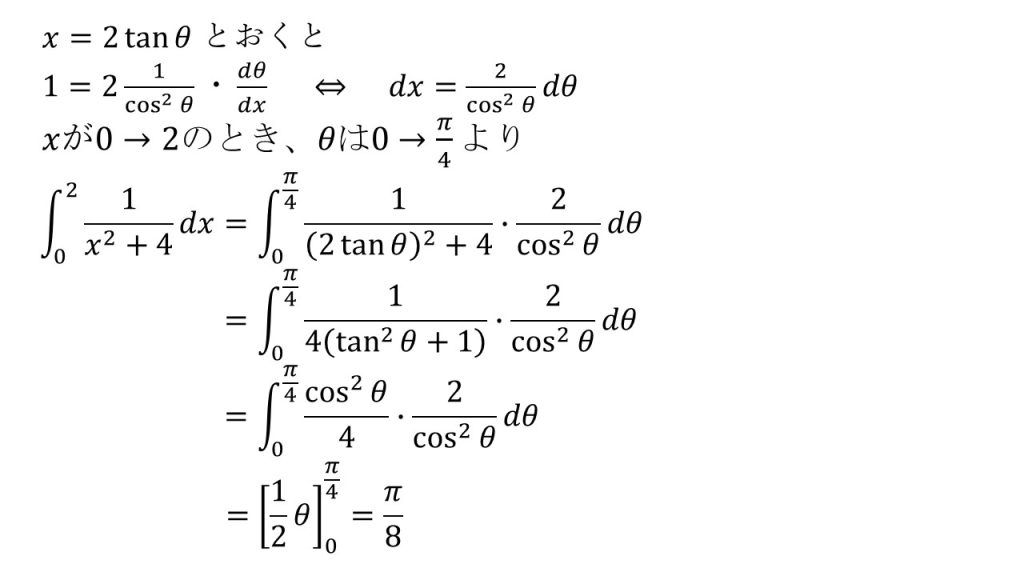
※分母がx²+〇→x=2tanθと置換すると上手くいく。これは特殊な置換なので覚えておこう！

⑥

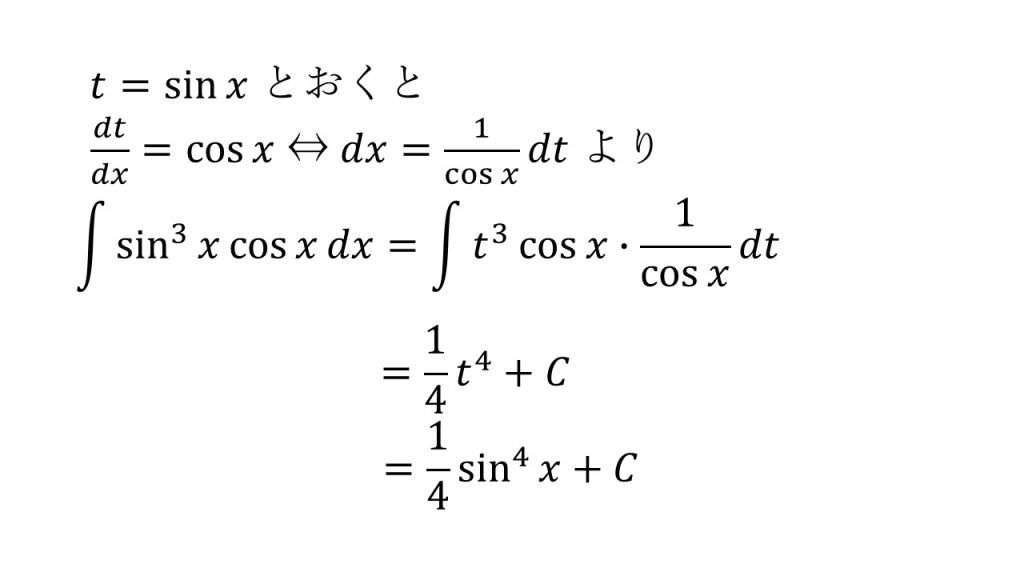
※「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。

⑦

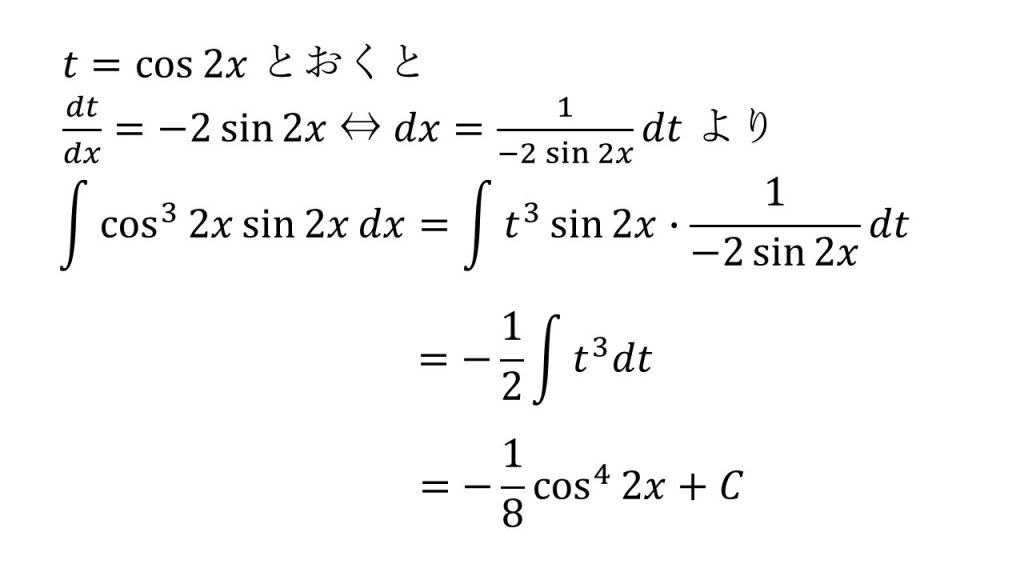
※「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。

⑧

※「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
※3倍角の公式を利用した解法もある→積分（数学Ⅲ）計算全パターン（三角関数）

⑨

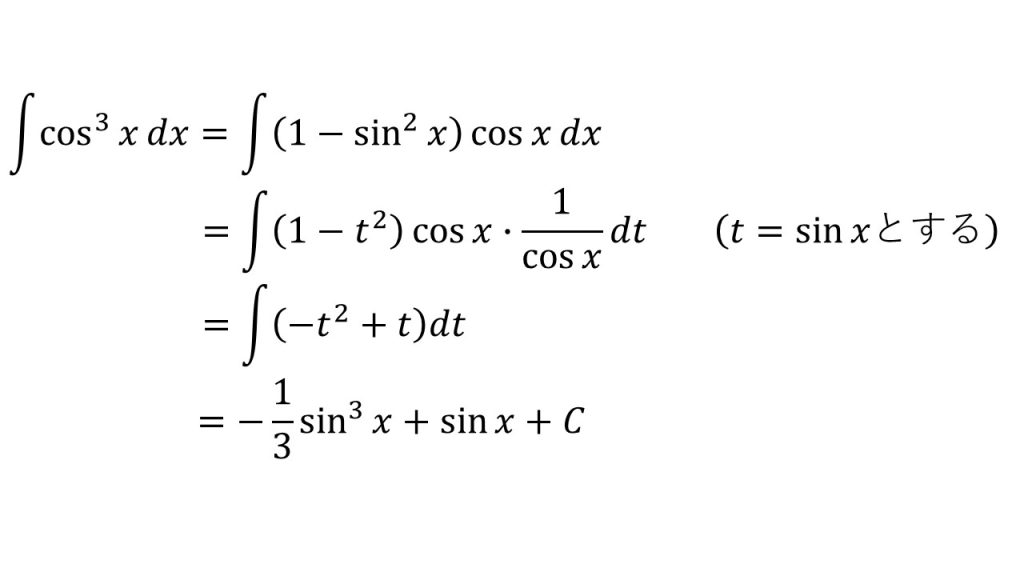
※「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
※3倍角の公式を利用した解法もある→積分（数学Ⅲ）計算全パターン（三角関数）

⑩

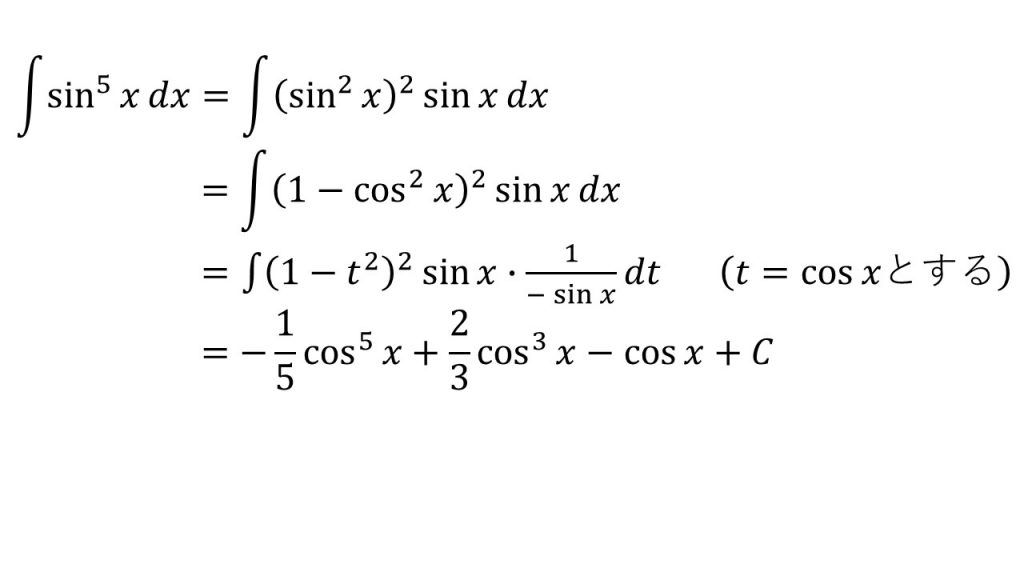
※「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。

⑪

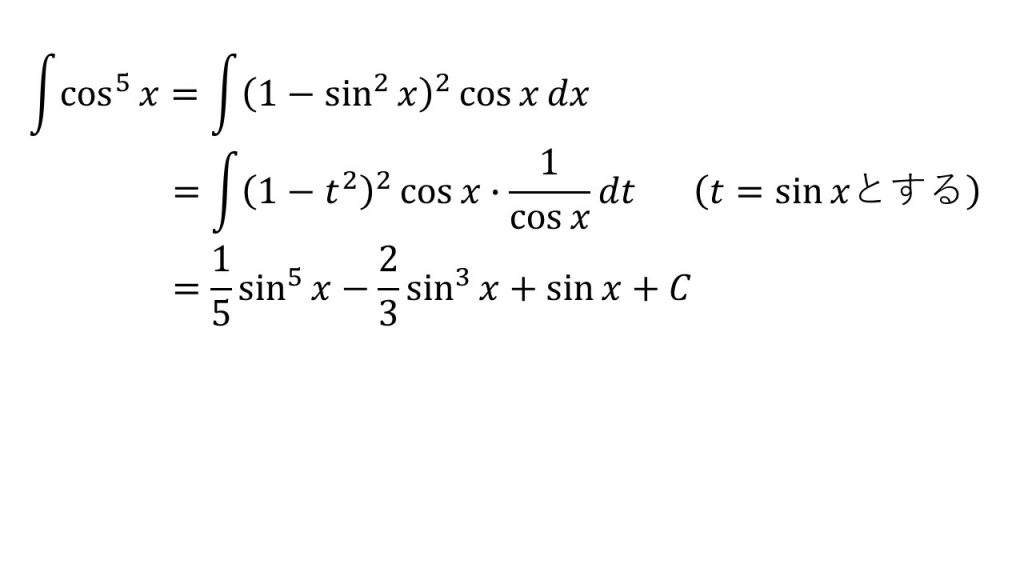
※「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。

⑫

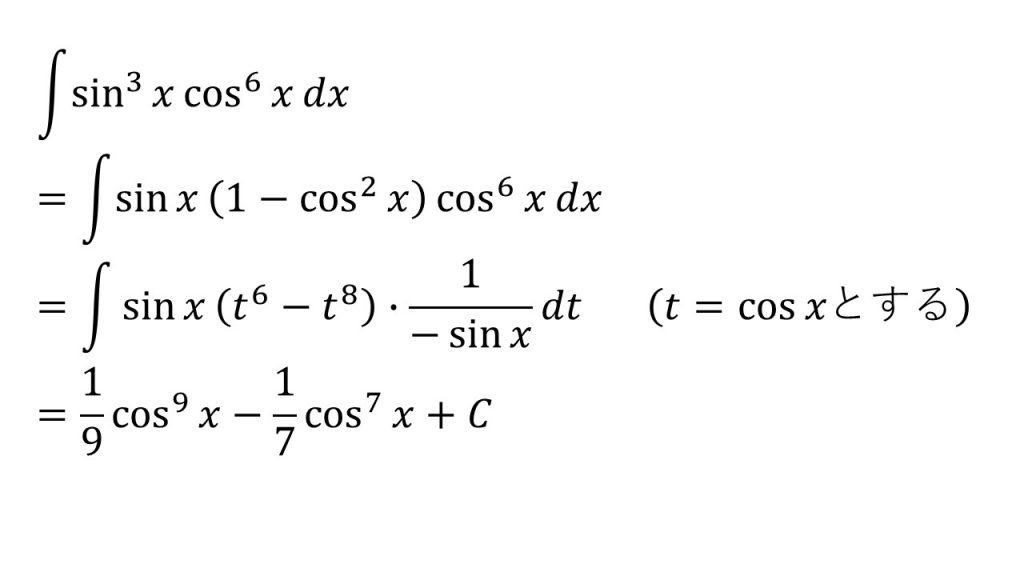
※「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。

⑬

※「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。

⑭

• 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
• 分数式の積分についてはこちら→分数式の積分
• logM－logN=logM/N→対数公式

⑮

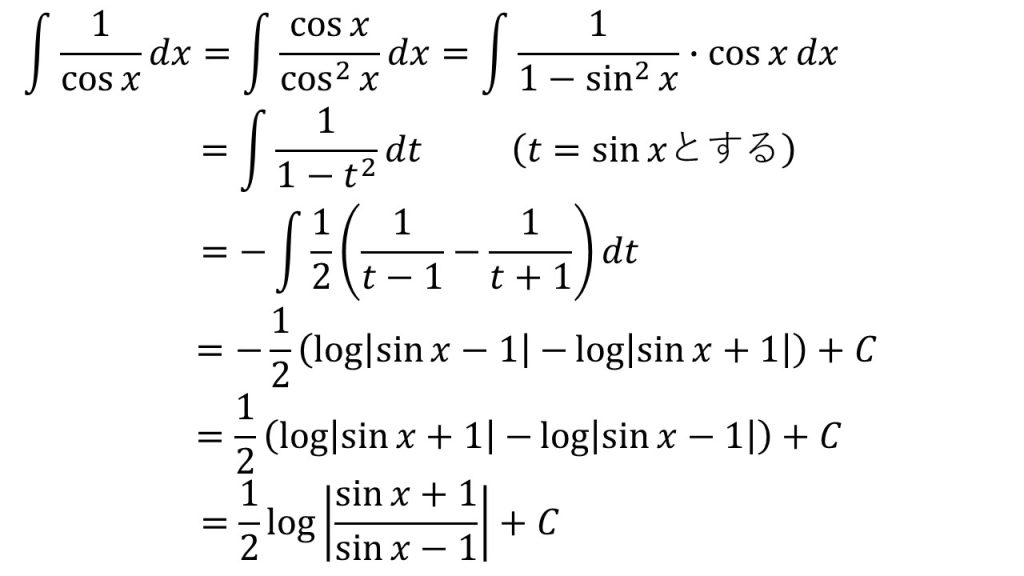
• 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
• 分数式の積分についてはこちら→分数式の積分
• logM－logN=logM/N→対数公式

⑯

• sin(π/2－θ)=cosθとなる。詳しくはこちら→三角関数の性質を単位円で理解する（θ+2nπ、−θ、π±θ、π/2±θ）
• 半角の公式（2倍角の公式の逆）を利用している→三角関数公式
• sinxで上手くいかないときは、x=π/2－θと置換して、cosθに変換することを考えてみる。
• インテグラルの前に－がついているときは、積分区間を反対にすることができる。

⑰

• sin(π/2－θ)=cosθとなる。詳しくはこちら→三角関数の性質を単位円で理解する（θ+2nπ、−θ、π±θ、π/2±θ）
• 半角の公式（2倍角の公式の逆）を利用している→三角関数公式
• sinxで上手くいかないときは、x=π/2－θと置換して、cosθに変換することを考えてみる。

⑱

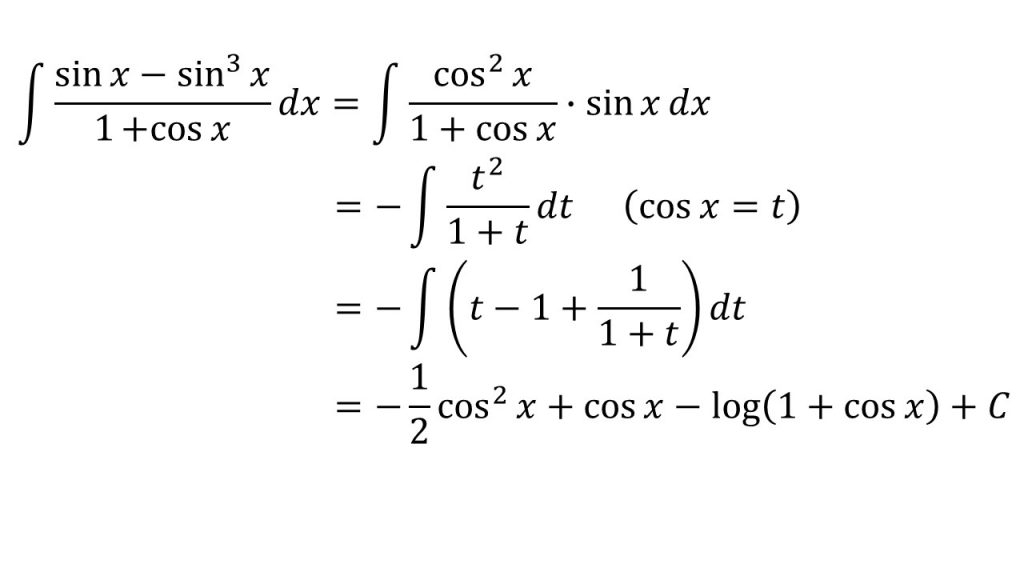
• 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
• 分数式の積分についてはこちら→分数式の積分

⑲

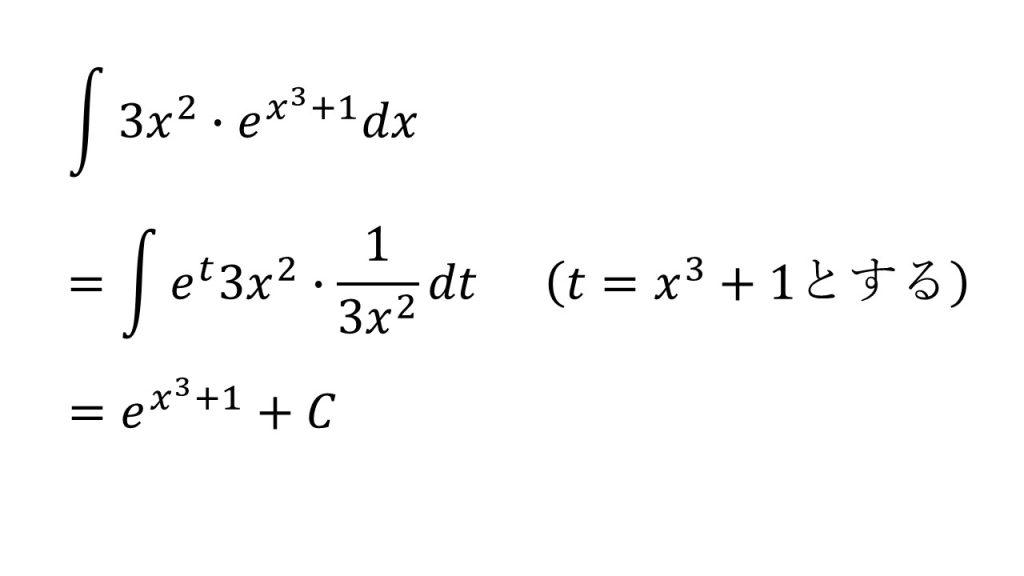
• 部分積分法では上手くいかない。
• x³+1の微分が3x²であると気がつけば、置換すれば上手くいくと気がつくことができる。

⑳

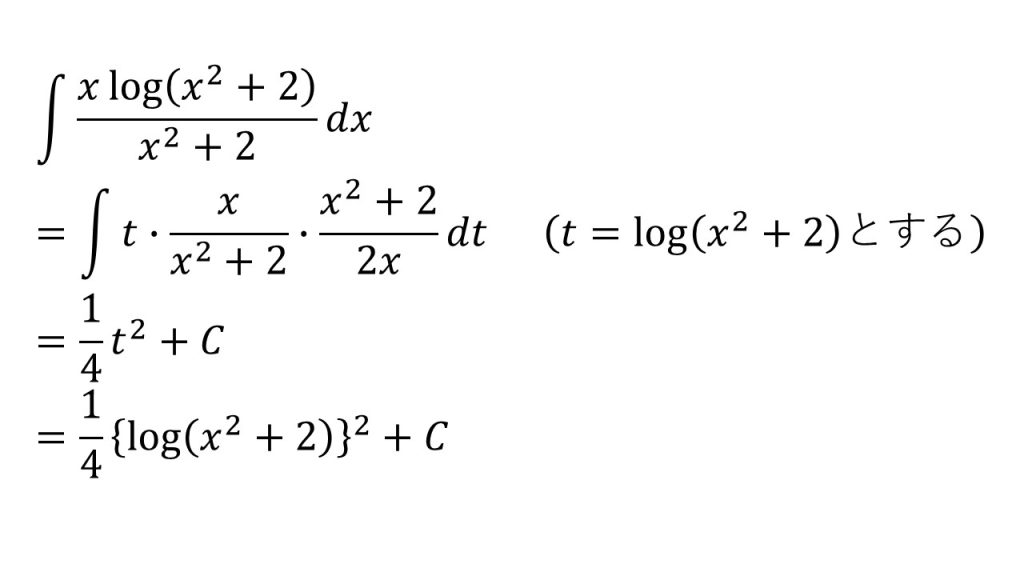
• t=x²+2としても上手くいかない。
• log(x²+2)の微分（合成関数の微分）が2x/(x²+2)であると気がつけば、t=log(x²+2)と置換すれば上手くいくと気がつくことができる。

---

☆問題のみはこちら→置換積分法（問題）

☆積分（数学Ⅲ）の計算公式一覧

---

【式の種類別演習問題一覧】

①積分（数学Ⅲ）計算全パターン（整式）

②積分（数学Ⅲ）計算全パターン（三角関数）

③積分（数学Ⅲ）計算全パターン（指数・対数）

④積分（数学Ⅲ）計算全パターン（異なる関数の積）

【パターン別演習問題一覧】

①合成関数の積分

②置換積分法

③分数式の積分

④部分積分法

---

～参考～

☆積分計算（数学Ⅲ）をマスターしよう（解説・授業・公式・演習問題一覧）

☆積分（数学Ⅲ）の計算公式一覧

☆積分（数学Ⅲ）の計算公式の証明はこちら→「積分は微分の逆である」ということを意識して積分の公式を理解しよう！

☆微分法（数学Ⅲ）の計算公式一覧

☆微分計算（数学Ⅲ）をマスターしよう（解説・授業・公式・演習問題一覧）

☆数学Ⅲ公式一覧

☆数学Ⅲの解説・授業・公式・演習問題一覧

☆数学の解説動画・授業動画一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学公式一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の解説・授業・公式・演習問題一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学典型パターン一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の語呂合わせ

☆数学学習に必要な参考書・問題集