☆問題のみはこちら→部分積分法(問題)
【公式】
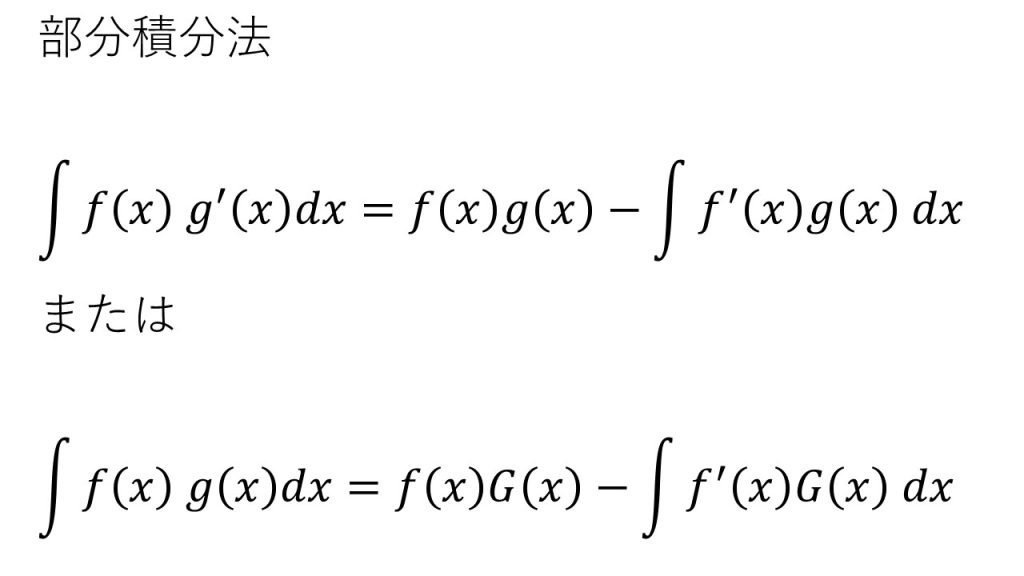
【公式の証明】
積の微分の公式から証明する。
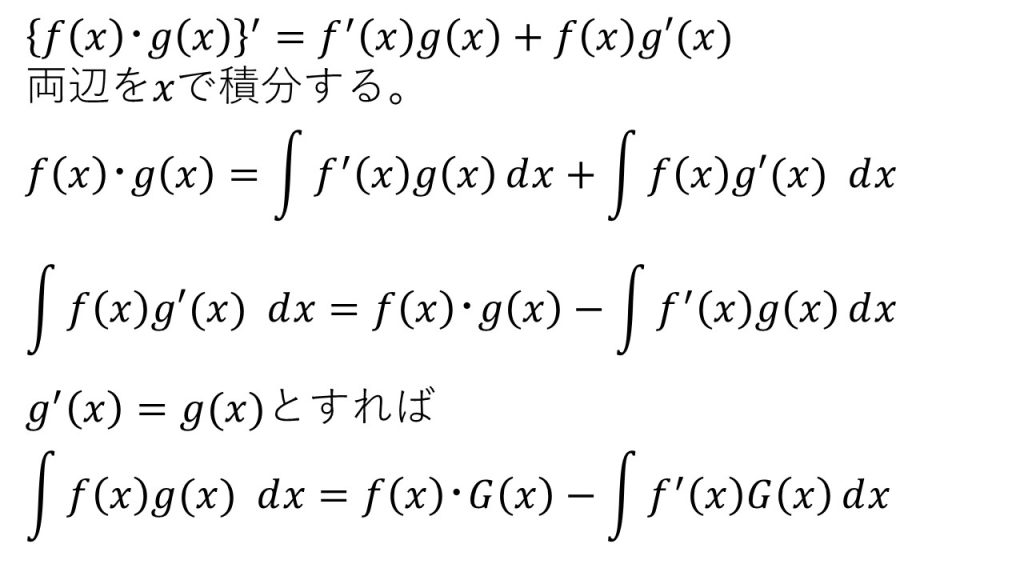
【使い方】
- 積分する関数が異なる関数の積の形となっているときに用いることが多い。
- logxは、1×logxと考えて部分積分法を利用して積分をする。このパターンは覚えておく。
- 微分すると簡単になるものをf(x)、指数関数や三角関数など(微分してもあまり形が変わらないもの)をg(x)とするとやりやすくなることが多い。
- 対数関数など積分しにくいものはf(x)にするとよい。(f(x)は積分しなくてもよいから。)
【例題】
①
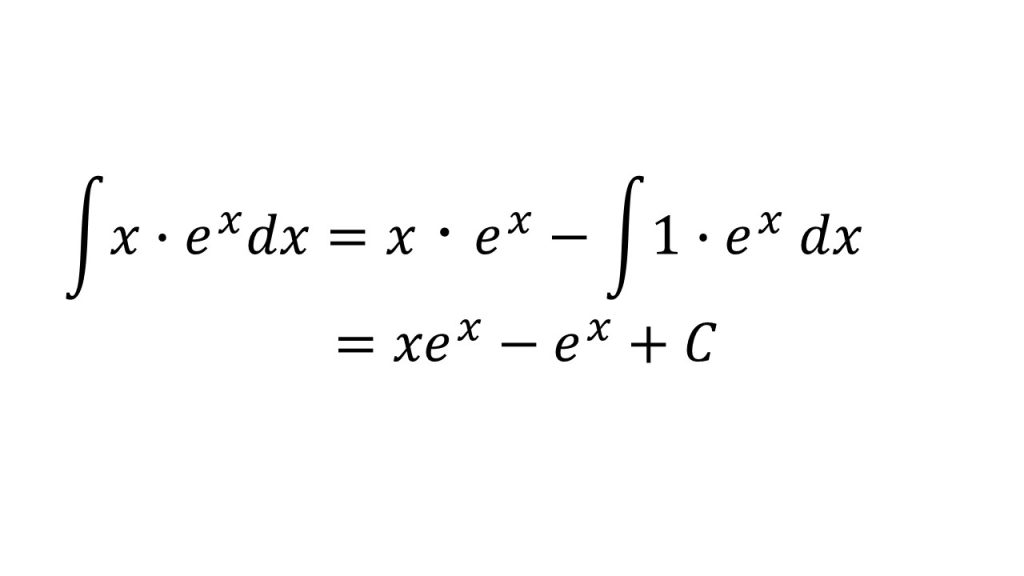
- xをf(x)(微分すると簡単になるもの)、exをg(x)(微分してもあまり形が変わらないもの)とする。
②
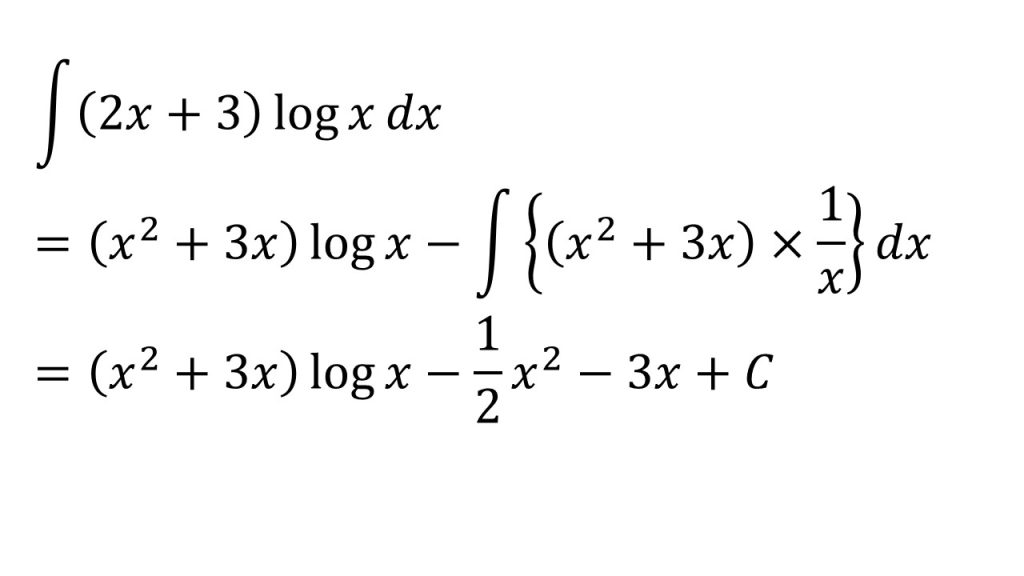
- logxは積分するのに部分積分法が必要になるので、logxは積分しなくてもよいf(x)に、積分が簡単な2x+3をg(x)とする。
③
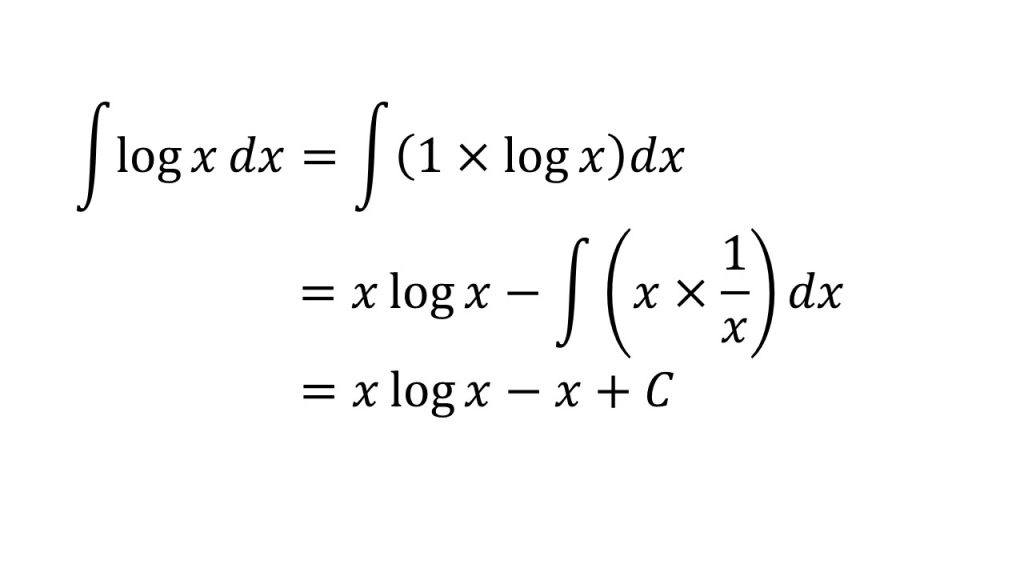
- 部分積分法を利用するために、logxを1×logxと考える。
- logxは積分がやりにくく、微分は分かりやすいので、公式のf(x)にする。(1をg(x)とする。)
④
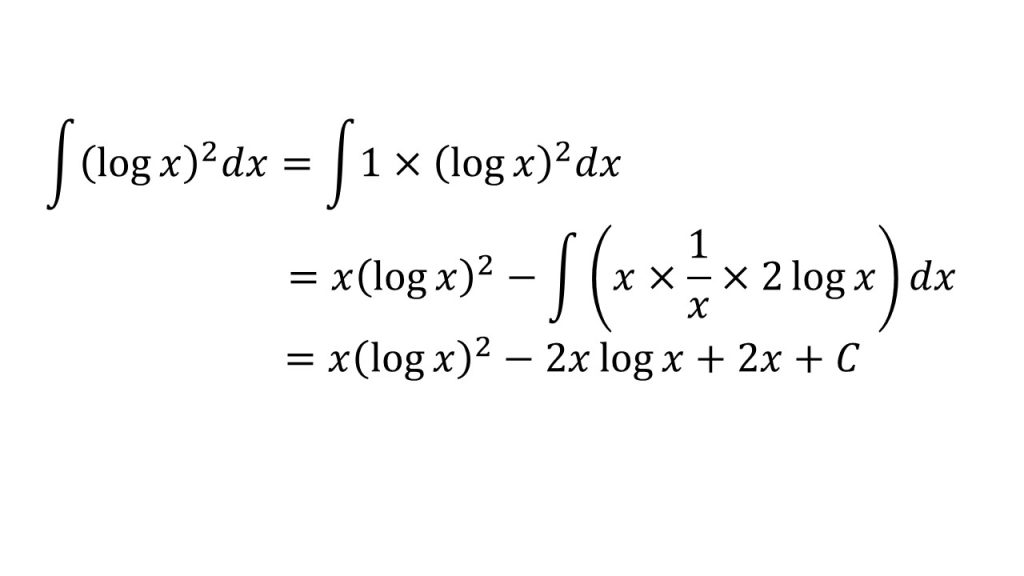
- 部分積分法を利用するために、(logx)2を1×(logx)2と考える。
- (logx)2は積分がよく分からず、微分は分かりやすいので、公式のf(x)にする。(1をg(x)とする。)
- (logx)2の微分は合成関数の微分→微分法(数学Ⅲ)公式
⑤
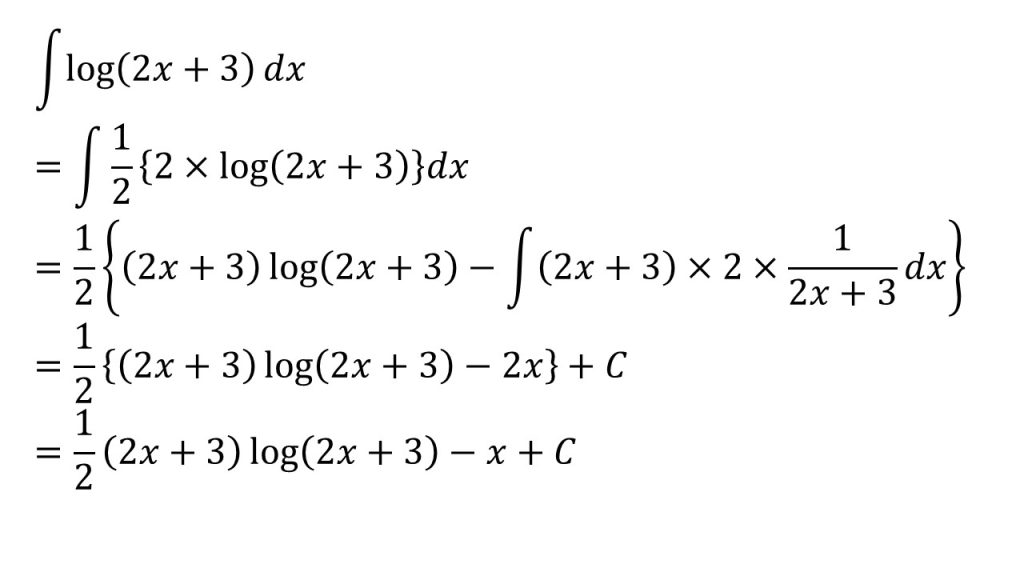
- 部分積分法を利用するために、log(2x+3)を2×log(2x+3)とする。つじつまを合わせるために1/2をかけるのを忘れないように。
- log(2x+3)は積分がよく分からず、微分は分かりやすいので、公式のf(x)にする。(2をg(x)とする。)
- 2x+3は2の原始関数の1つなので、2を不定積分したときは、2x+3としてよい。
- log(2x+3)の微分は合成関数の微分→微分法(数学Ⅲ)公式
⑥
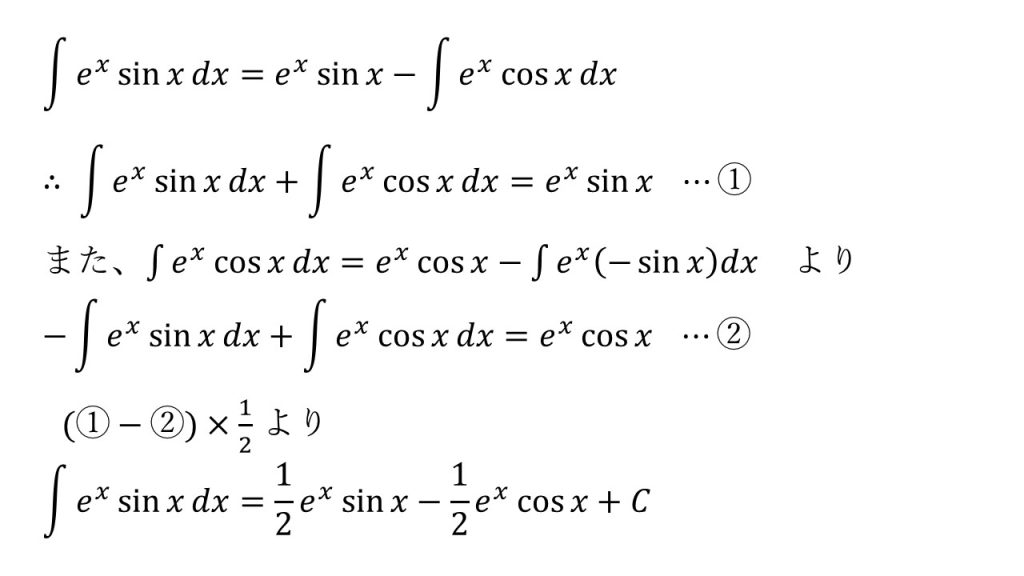
- 部分積分法を用いると、∫exsinxdxと∫excosxdxという形が繰り返し現れることに気がつく(同形反復)。このような場合は、連立させると上手くいく。
☆問題のみはこちら→部分積分法(問題)
【式の種類別演習問題一覧】
【パターン別演習問題一覧】
~参考~
☆積分計算(数学Ⅲ)をマスターしよう(解説・授業・公式・演習問題一覧)
☆積分(数学Ⅲ)の計算公式の証明はこちら→「積分は微分の逆である」ということを意識して積分の公式を理解しよう!
☆微分計算(数学Ⅲ)をマスターしよう(解説・授業・公式・演習問題一覧)
