☆問題のみはこちら→積分(数学Ⅲ)計算全パターン(三角関数)(問題)
①

- 公式を利用しよう→積分法(数学Ⅲ)公式
- 「積分は微分の逆である」ということを意識すれば符号のミスも防げる→「積分は微分の逆である」ということを意識して積分の公式を理解しよう!
②
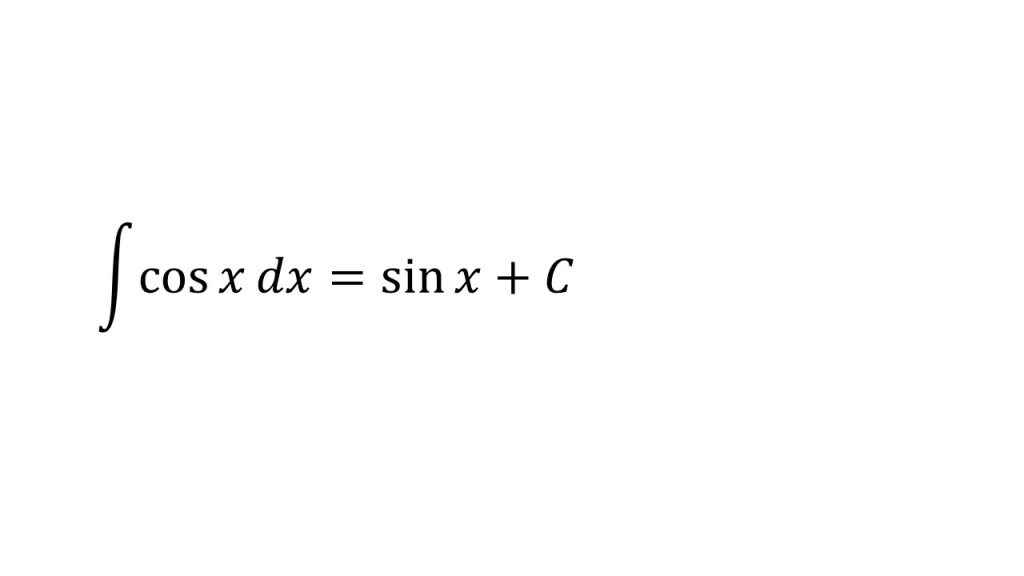
- 公式を利用しよう→積分法(数学Ⅲ)公式
- 「積分は微分の逆である」ということを意識すれば符号のミスも防げる→「積分は微分の逆である」ということを意識して積分の公式を理解しよう!
③
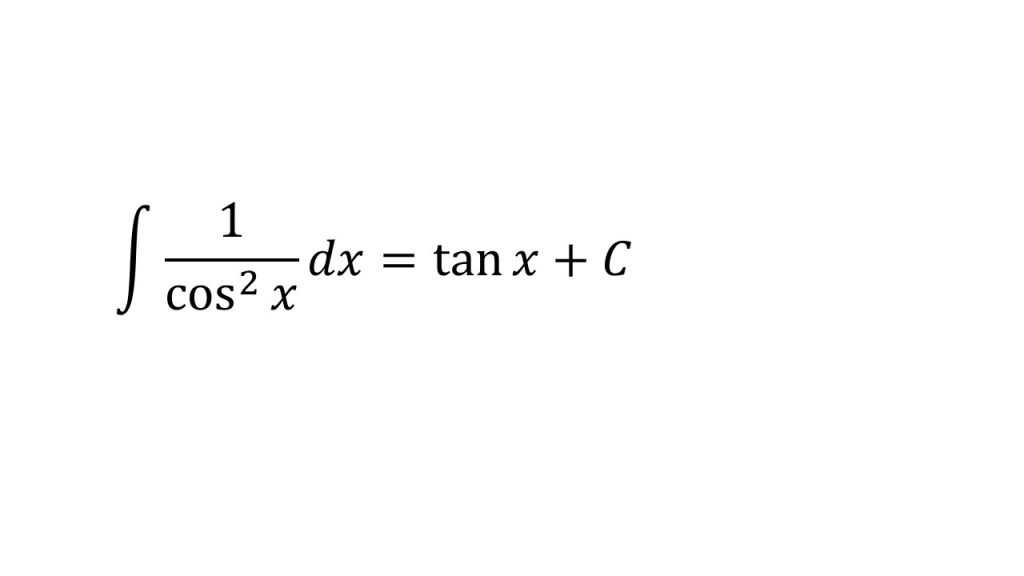
- 公式を利用しよう→積分法(数学Ⅲ)公式
- 「積分は微分の逆である」ということを意識すれば、これがなぜ成り立つかが理解できる→「積分は微分の逆である」ということを意識して積分の公式を理解しよう!
④
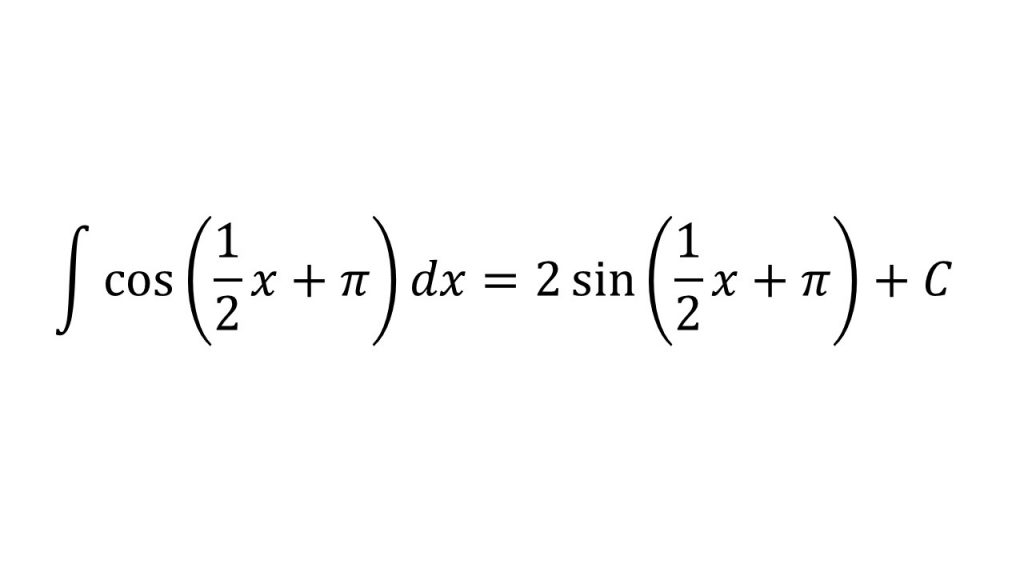
- cos(1/2x+π)が合成関数であることに注意。合成関数の積分についてはこちら→合成関数の積分
⑤
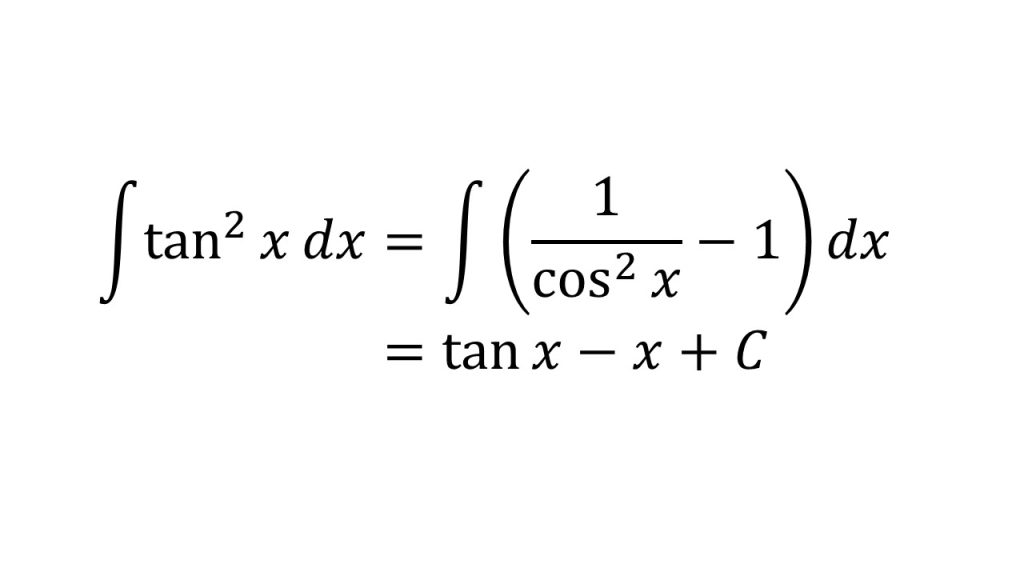
- 1+tan2θ=1/co2θという三角関数の公式を利用している→三角関数公式
⑥

⑦
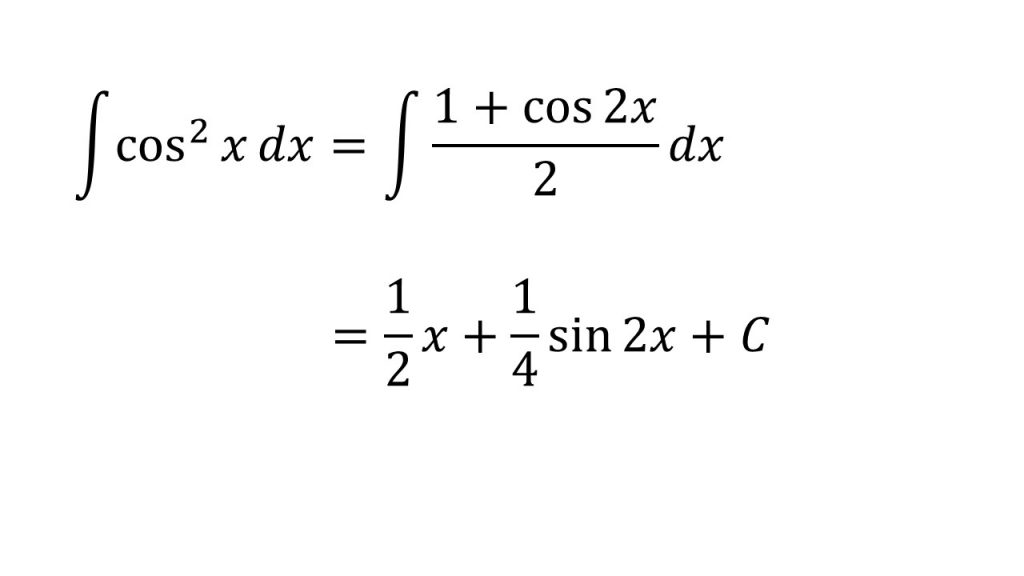
⑧
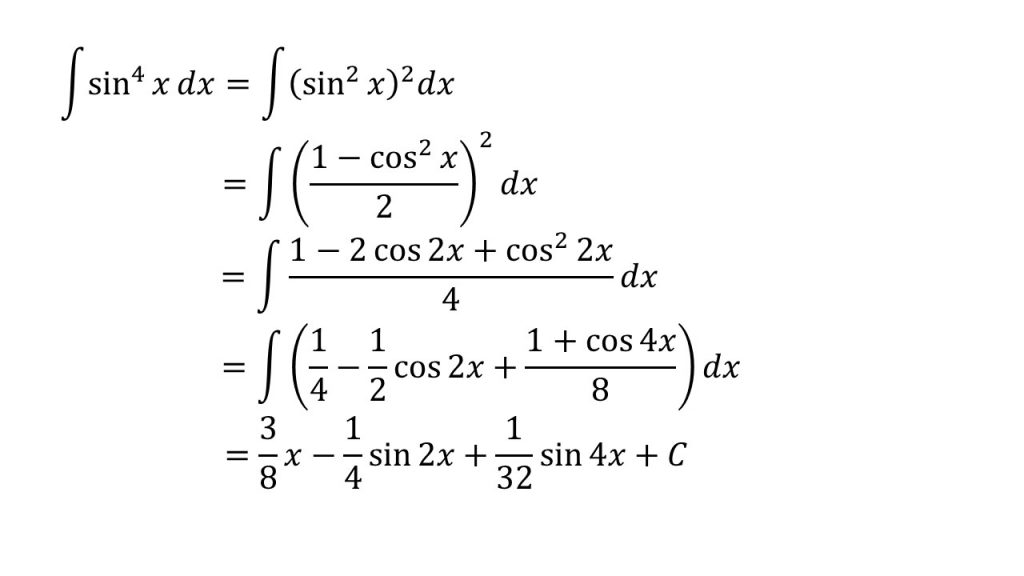
⑨
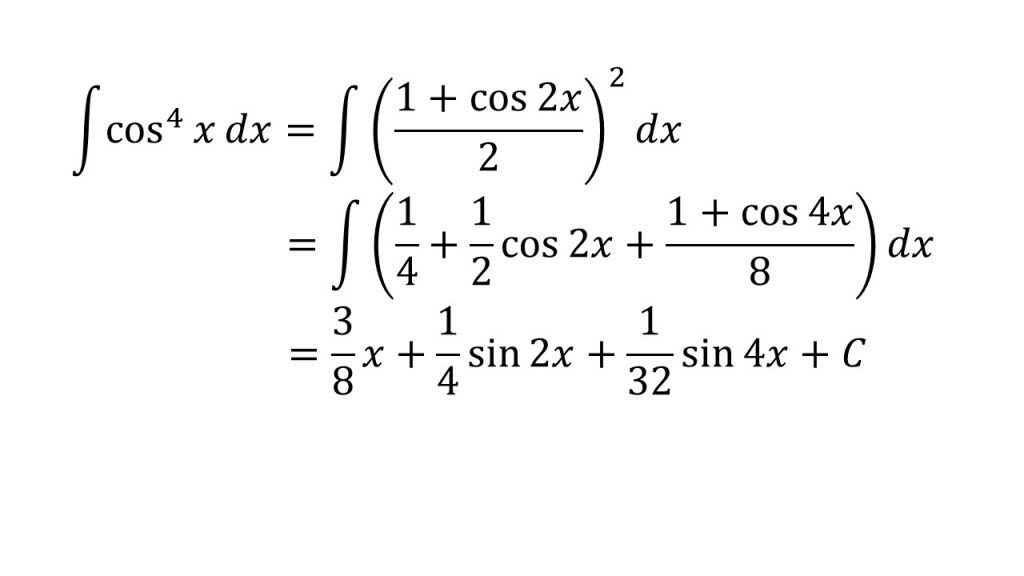
⑩
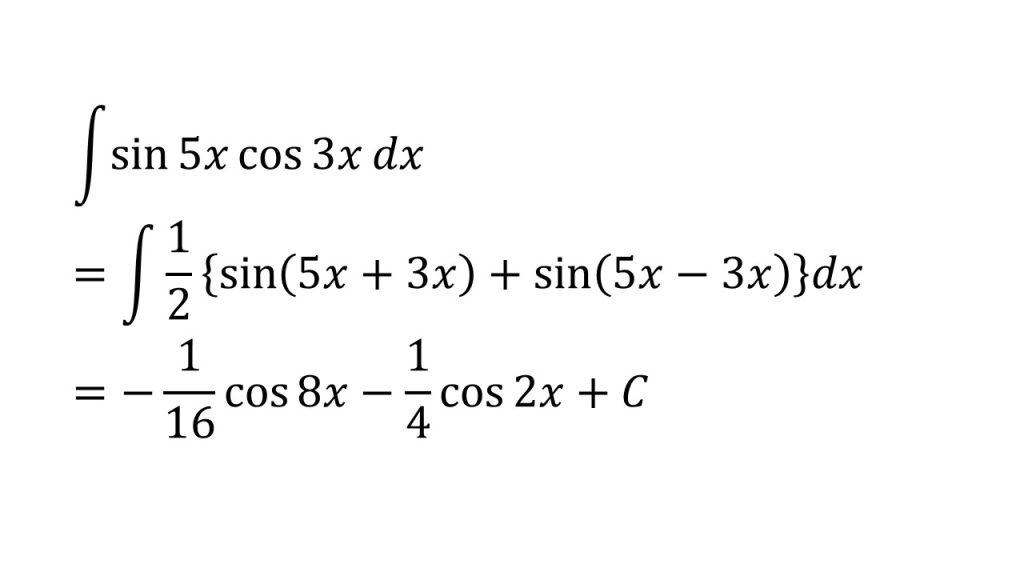
⑪
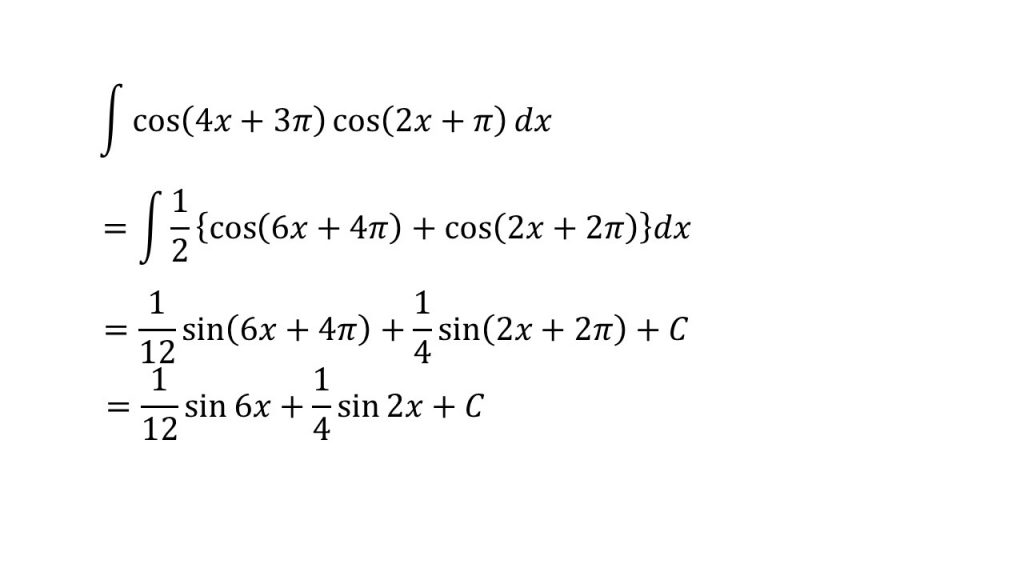
- 積和の公式を利用している→三角関数公式
- sin(6x+4π), sin(2x+2π)は合成関数であることに注意。合成関数の積分についてはこちら→合成関数の積分
- sin(6x+4π)=sin6x, sin(2x+2π)=sin2xとなる。詳しくはこちら→三角関数の性質を単位円で理解する(θ+2nπ、−θ、π±θ、π/2±θ)
⑫
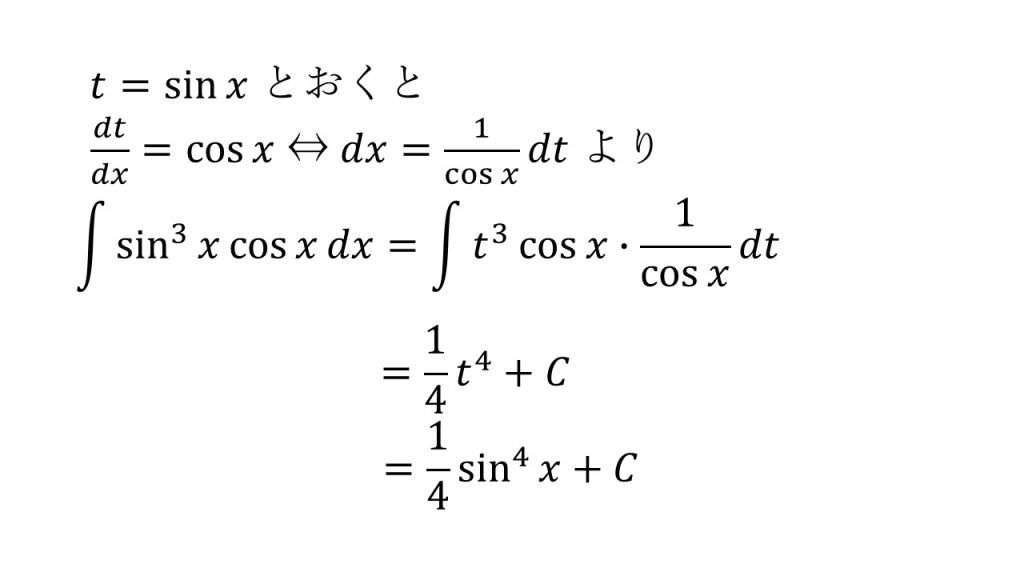
- 置換積分法
- 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
⑬
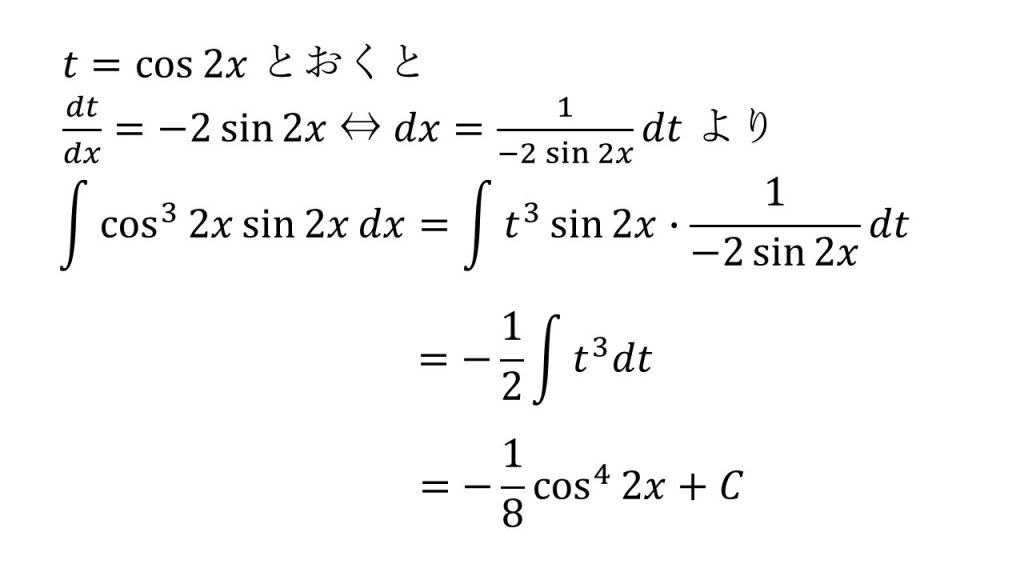
- 置換積分法
- 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
⑭

- 置換積分法
- 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
【別解】3倍角の公式を利用
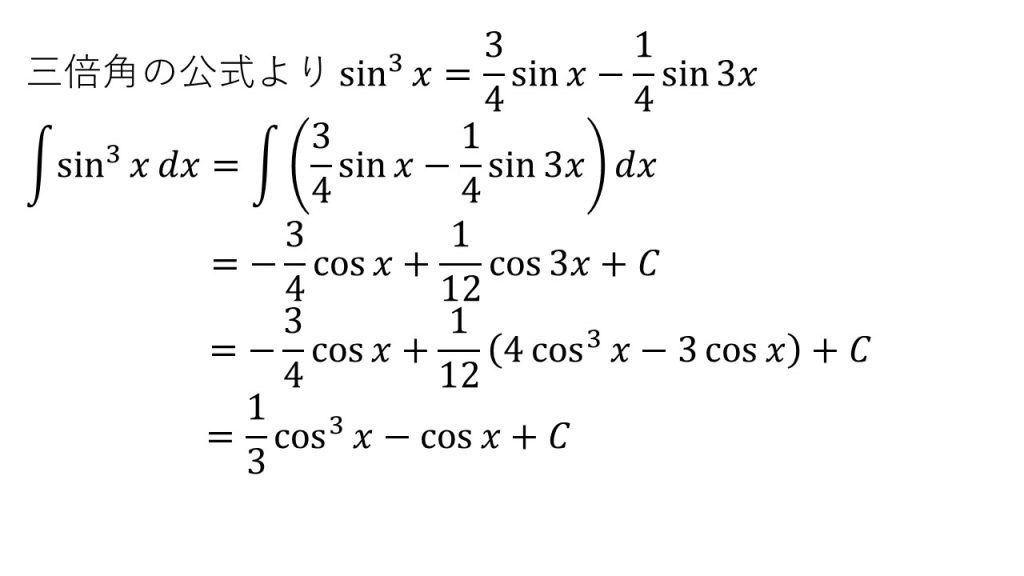
- 3倍角の公式を覚えているのであれば、3倍角の公式を利用した方が速く解けることがある。3倍角の公式についてはこちら→3倍角の公式の導出
⑮
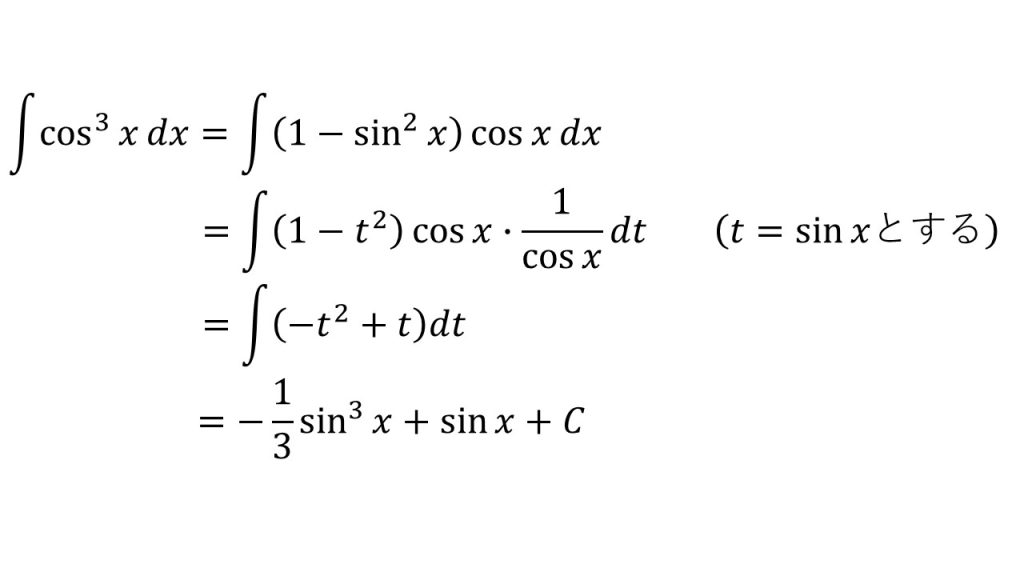
- 置換積分法
- 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
【別解】三倍角の公式を利用

- 3倍角の公式を覚えているのであれば、3倍角の公式を利用した方が速く解けることがある。3倍角の公式についてはこちら→3倍角の公式の導出
⑯
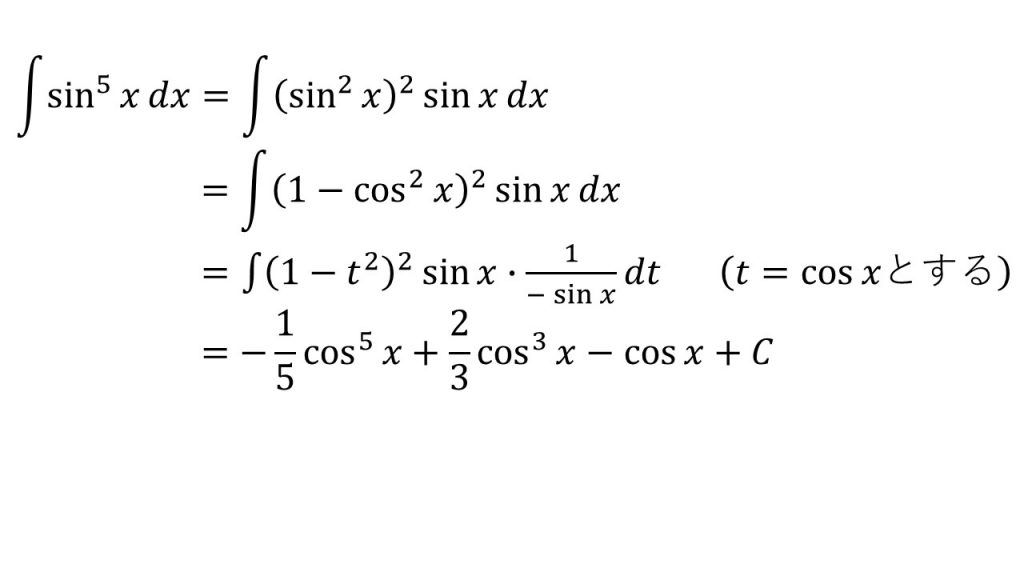
- 置換積分法
- 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
⑰
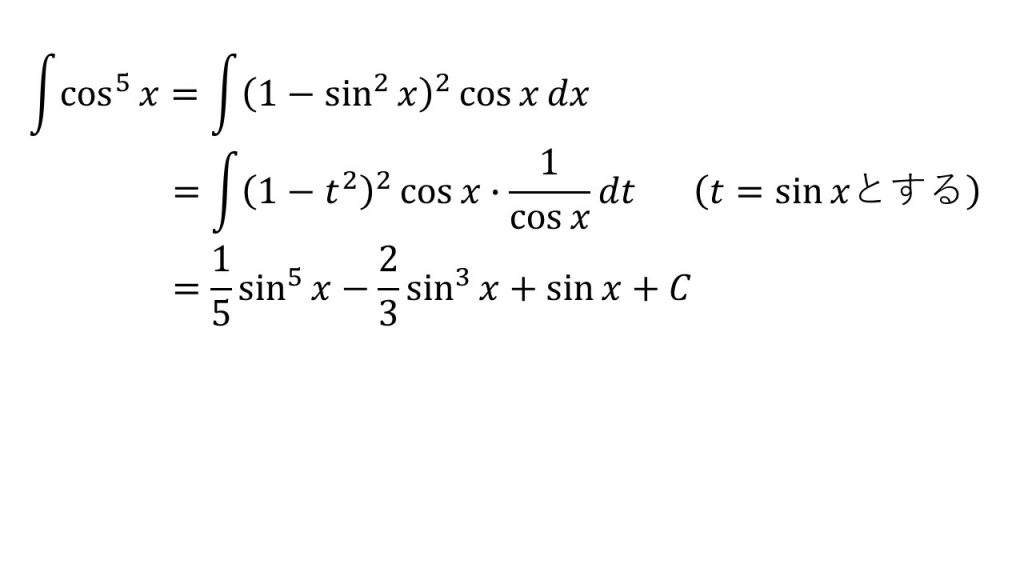
- 置換積分法
- 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
⑱
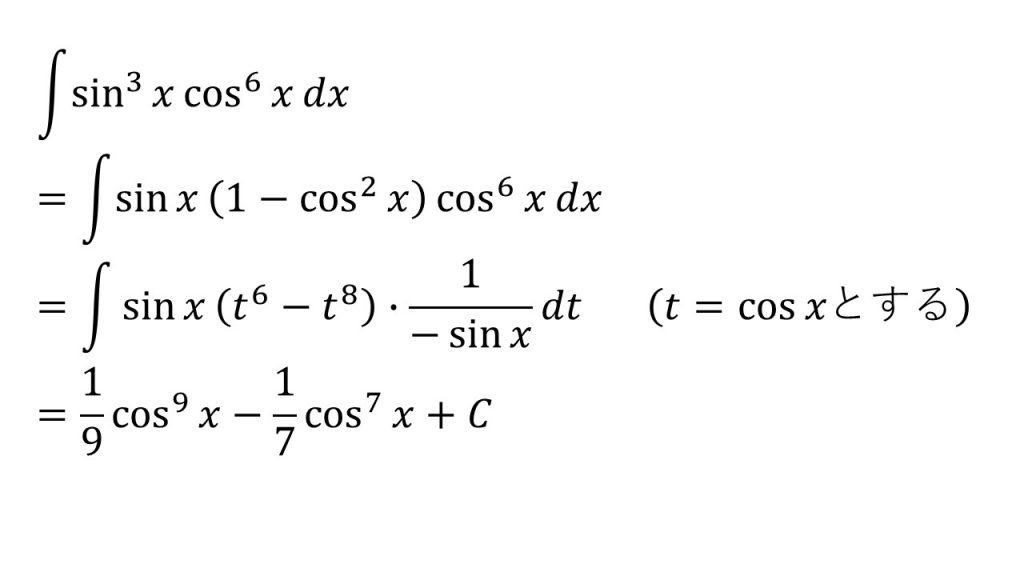
- 置換積分法
- 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
⑲

- 置換積分法
- 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
⑳

- f'(x)/f(x)の形にするパターン。なぜこれが成り立つか分からなければ、logf(x)を微分してみるとよい(対数関数の微分+合成関数の微分)。
㉑
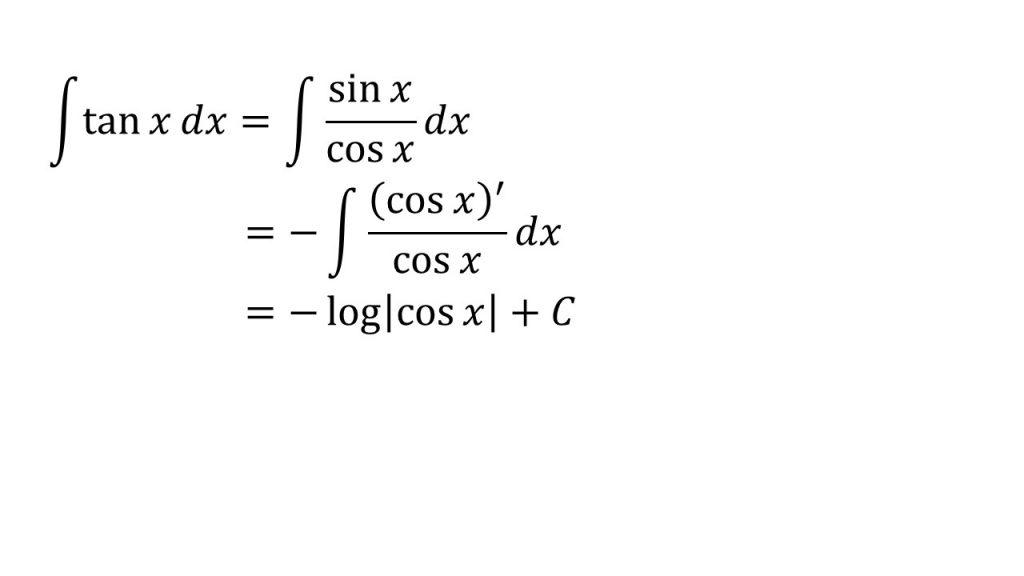
- f'(x)/f(x)の形にするパターン。なぜこれが成り立つか分からなければ、logf(x)を微分してみるとよい(対数関数の微分+合成関数の微分)。
㉒

- 定積分で表された関数の微分をしている→積分法の応用(数学Ⅲ)公式
- 簡単にいうと、「積分した後、微分すれば元に戻る」ということ。
- ただし、※でも書いているが、積分区間にxを含む場合、合成関数の微分を使うのを忘れないようにしないといけない。F(sinx), F(cosx)は合成関数のため、F'(sinx)-F'(cosx)=f(sinx)-f(cosx)としてはいけない。
㉓

- 置換積分法
- 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
- 分数式の積分についてはこちら→分数式の積分
- logM-logN=logM/N→対数公式
㉔
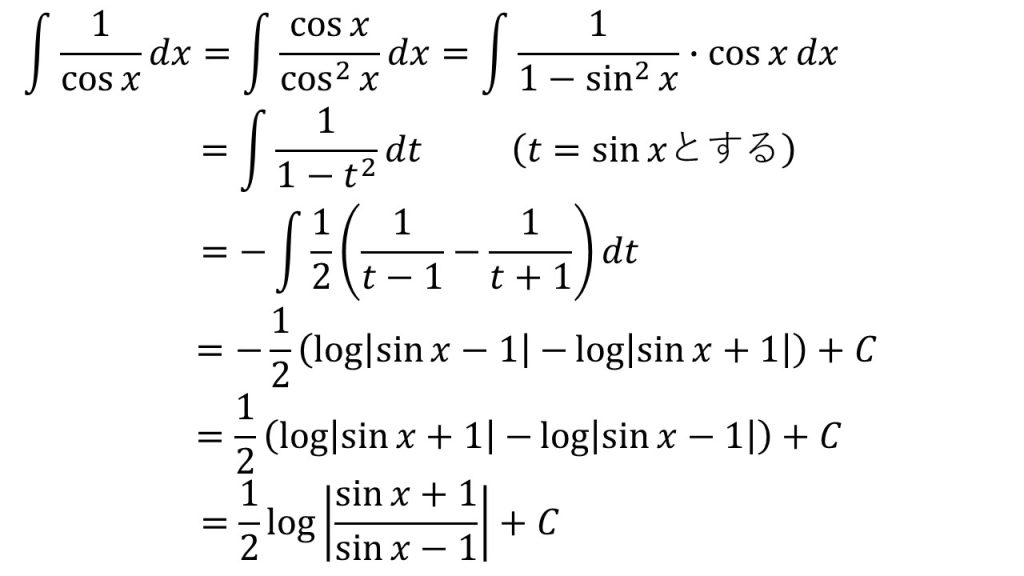
- 置換積分法
- 「t=sinxとすると1/cosxを作ることができ、t=cosxとすると1/sinxを作ることができる」ということを意識すると上手くいく。
- 分数式の積分についてはこちら→分数式の積分
- logM-logN=logM/N→対数公式
㉕
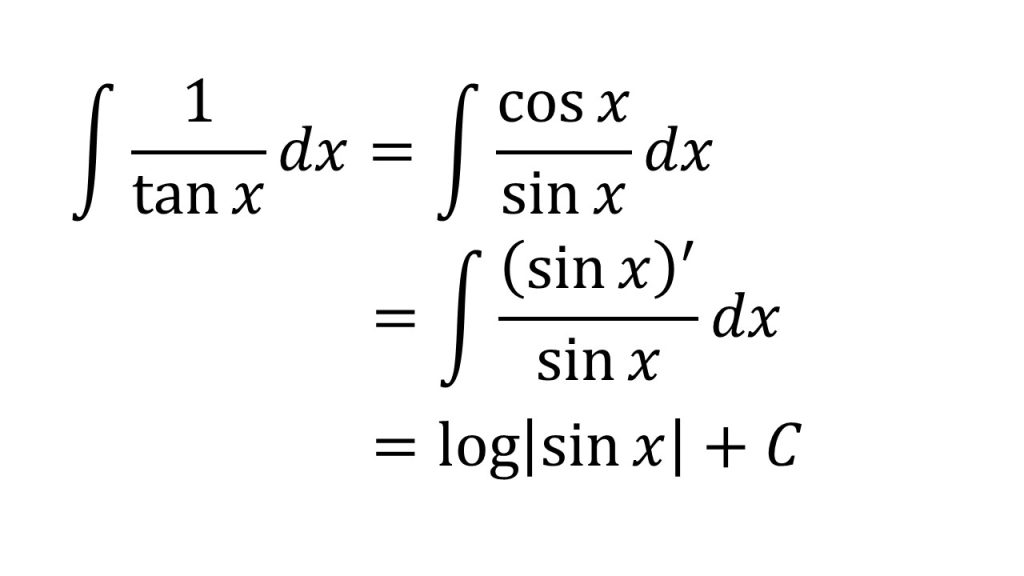
- f'(x)/f(x)の形にするパターン。なぜこれが成り立つか分からなければ、logf(x)を微分してみるとよい(対数関数の微分+合成関数の微分)。
㉖
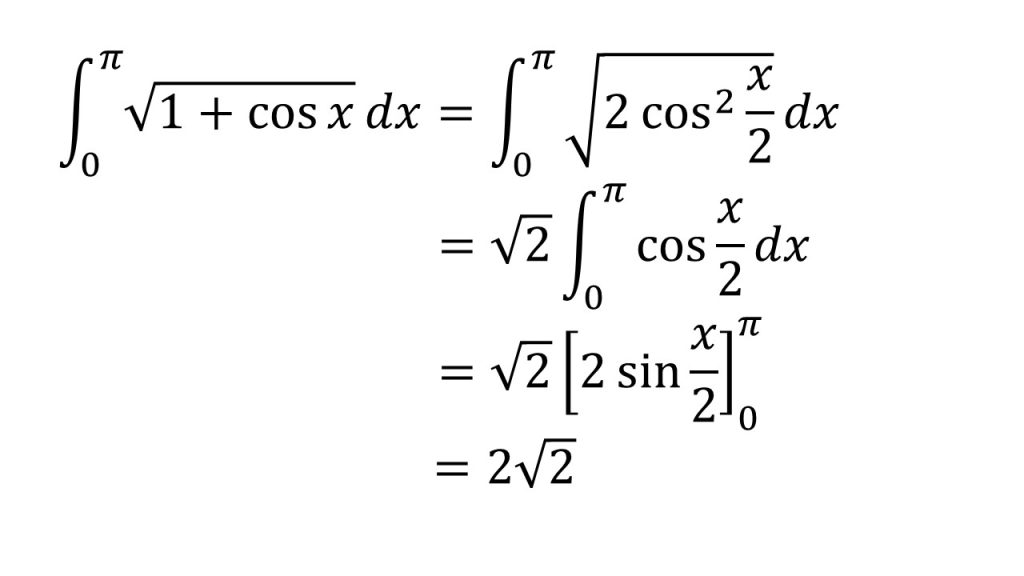
㉗
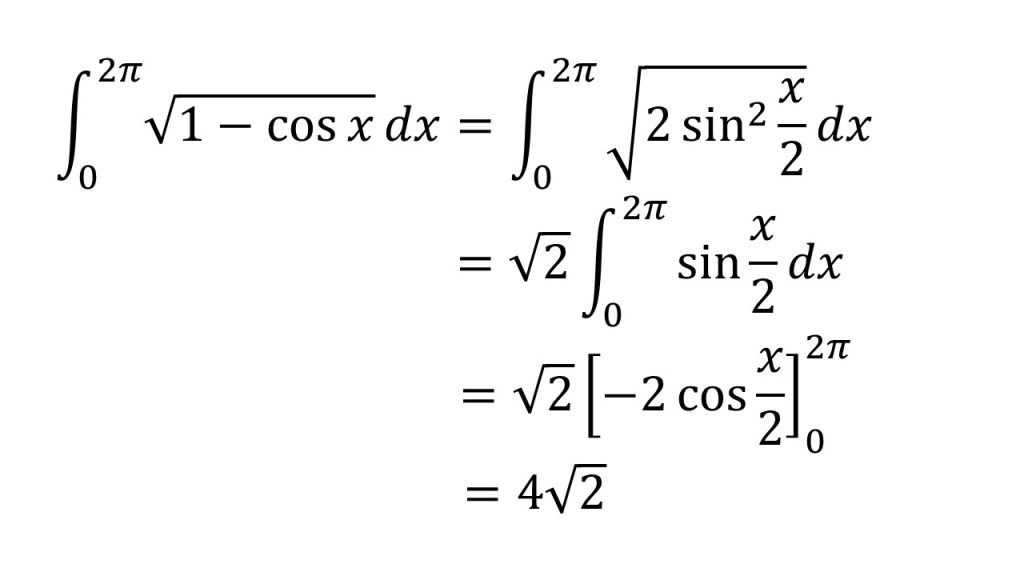
㉘

- sin(π/2-θ)=cosθとなる。詳しくはこちら→三角関数の性質を単位円で理解する(θ+2nπ、−θ、π±θ、π/2±θ)
- 半角の公式(2倍角の公式の逆)を利用している→三角関数公式
- sinxで上手くいかないときは、x=π/2-θと置換して、cosθに変換することを考えてみる。置換積分法についてはこちら→置換積分法
- インテグラルの前に-がついているときは、積分区間を反対にすることができる。
㉙

- 公式を利用しよう→積分法(数学Ⅲ)公式
- 「積分は微分の逆である」ということを意識すれば、これがなぜ成り立つかが理解できる→「積分は微分の逆である」ということを意識して積分の公式を理解しよう!
㉚

- sin(π/2-θ)=cosθとなる。詳しくはこちら→三角関数の性質を単位円で理解する(θ+2nπ、−θ、π±θ、π/2±θ)
- 半角の公式(2倍角の公式の逆)を利用している→三角関数公式
- sinxで上手くいかないときは、x=π/2-θと置換して、cosθに変換することを考えてみる。置換積分法についてはこちら→置換積分法
㉛
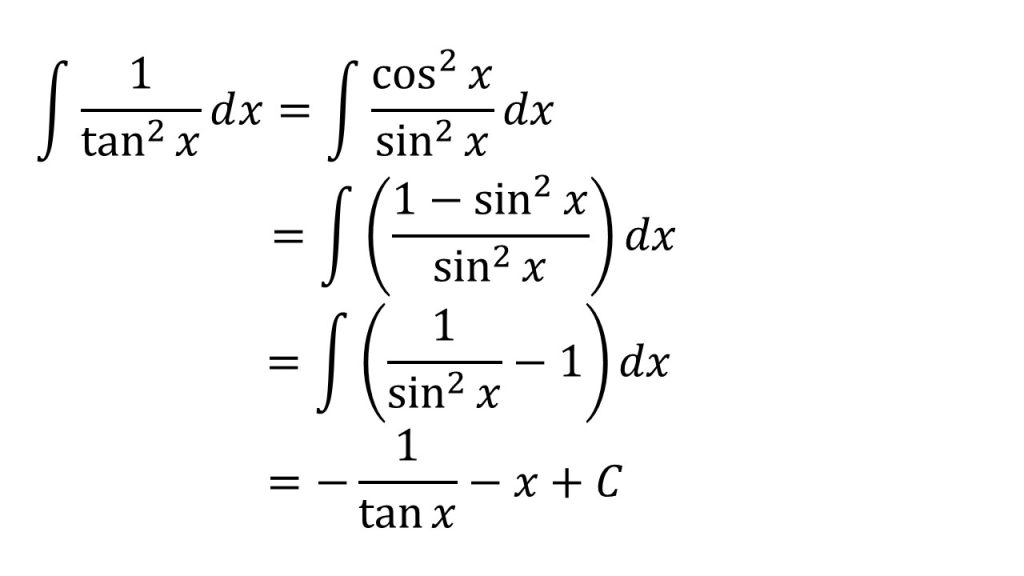
- tanxを含んだ式の積分で困ったら、tanx=sinx/cosxを利用しよう→三角関数公式
㉜
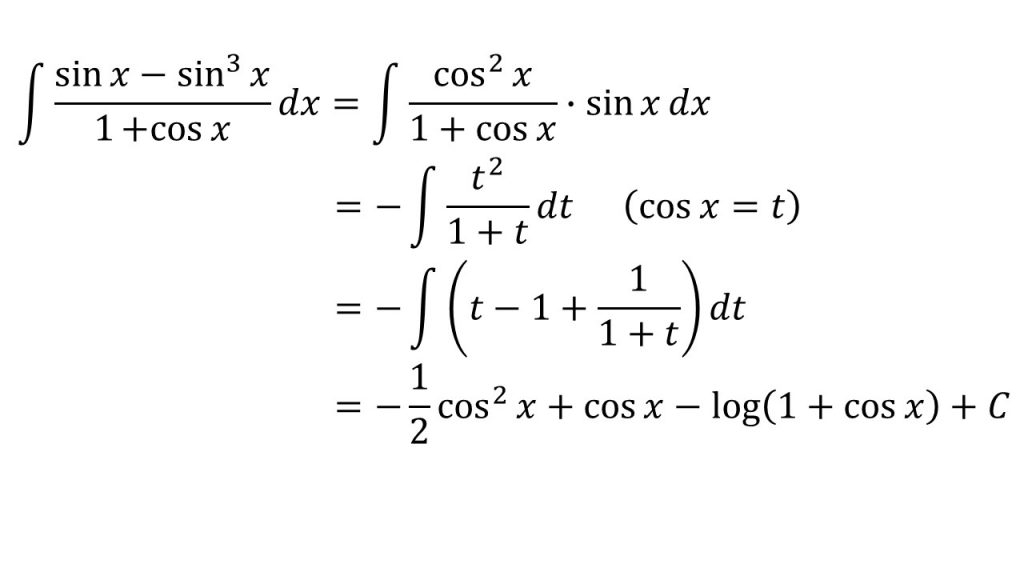
☆問題のみはこちら→積分(数学Ⅲ)計算全パターン(三角関数)(問題)
【式の種類別演習問題一覧】
【パターン別演習問題一覧】
~参考~
☆積分計算(数学Ⅲ)をマスターしよう(解説・授業・公式・演習問題一覧)
☆積分(数学Ⅲ)の計算公式の証明はこちら→「積分は微分の逆である」ということを意識して積分の公式を理解しよう!
☆微分計算(数学Ⅲ)をマスターしよう(解説・授業・公式・演習問題一覧)
