(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
溶解平衡とはどのような状態か?
今回は溶解平衡あるいは溶解度積の解説をします。まずはそもそも溶解平衡とはどのような状態なのか確認します。
溶解平衡とは、結晶から溶媒中へ溶け出すイオンの数と、溶液中から結晶に戻る(析出する)イオンの数が等しくなる状態のことです。
例えば、下図のように水の中で塩化銀が沈殿しているとき、この塩化銀の表面では銀イオンと塩化物イオンとなって水に溶け出していたり、逆に、溶液中に銀イオンや塩化物イオンがくっついて塩化銀の沈殿となっていたりします。
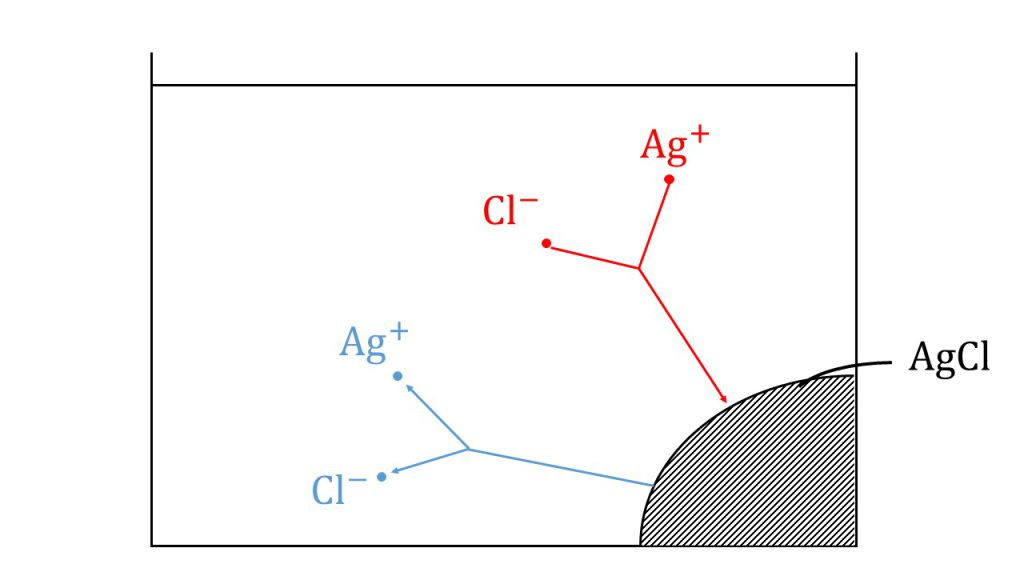
このとき溶け出すイオンの数つまり溶け出す速さと、析出するイオンの数つまり析出する速さが等しくなったときを溶解平衡というのですが、こうなると溶け出した分だけ析出するので、外からみると見かけ上、溶解が停止しているように見えます。
つまり、沈殿が形成されるとその沈殿では反応が起きていないように見えるのですが、それはあくまで「見かけ上」なので、実際はミクロな視点で見てみると絶えず反応は続いているのです。
溶解平衡(溶解度積)の計算の対象
それでは次は、溶解平衡の計算の対象となっているものについての解説をします。
溶解平衡の計算問題において扱う物質は、基本的に難溶性の塩を扱います。
難溶性の塩とは、塩化銀や塩化鉛や硫化銅や水酸化鉄や炭酸カルシウムや硫酸バリウムなど水に溶けにくい塩のことで、無機化学で「沈殿を形成する塩」として学習するものが対象となります。これらの塩は水に溶けにくいので、例えば、銀イオンと塩化物イオンを水に溶かすとそのほとんどが塩化銀となって沈殿します。
しかし、水に溶けにくいといっても水溶液中のイオンが全て沈殿になるわけではなく、ごくわずかではありますが、銀イオンや塩化物イオンは水溶液中にイオンとして存在しています。
溶解度積の導出
次に、溶解度積を平衡定数を使って導いてみようと思います。
例えば、塩化銀が下図のように水溶液中で沈殿を形成し、溶解平衡の状態になったとします。
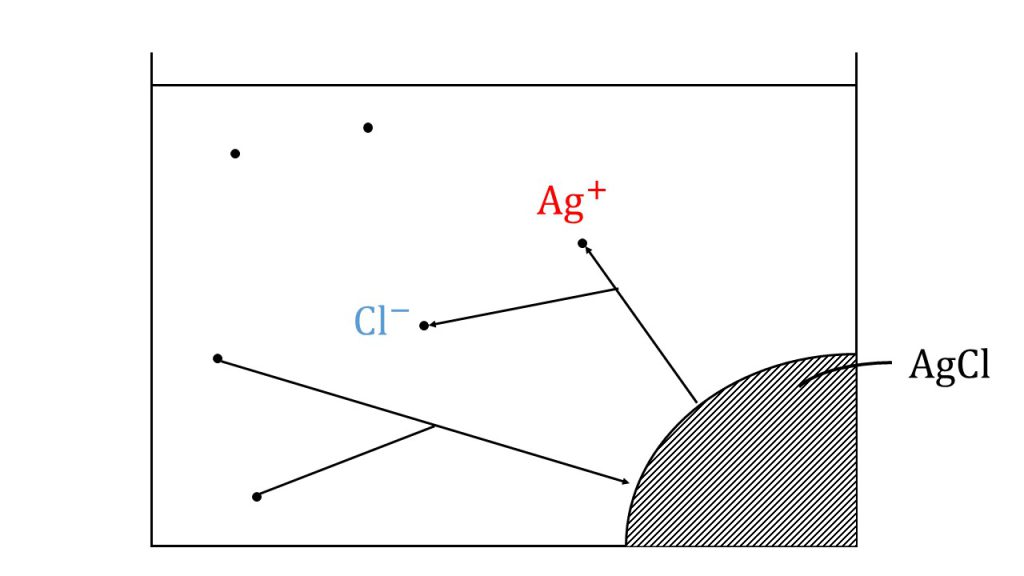
先ほども確認した通り、一見反応が止まったように見えますが、実際は溶解と析出を絶えず行なっています。そのため式で書くと、
AgCl(固) ⇆ Ag++Cl-
のようになります。塩化銀の沈殿は溶解して銀イオンと塩化物イオンになり、かつ、銀イオンと塩化物イオンはくっついて塩化銀の結晶として析出します。この反応は平衡状態となっているので、この平衡の平衡定数を定義によって導くと、
K=[Ag+][Cl-]/[AgCl(固)]
となります。ここで分母の塩化銀の結晶のモル濃度を両辺にかけてみます。
K[AgCl(固)]=[Ag+][Cl-]
すると、塩化銀の結晶のモル濃度は定数扱することができるので、この式の左辺K[AgCl(固)]はまとめて定数とみることができます。
- K[AgCl(固)]をまとめて定数扱いすることができる理由を、動画では「結晶となって沈殿している塩化銀の量は、水溶液中に存在するイオンの量に比べて非常に多く(塩化銀は難溶性の塩であるため)、溶解による塩化銀の量の変化は無視できるものだから」としています。
- ただ『化学の新研究』(三省堂)では、「固体では銀イオンと塩化物イオンが規則正しく配列しているので、そのモル濃度(固体1L中に含まれるイオンの物質量)は一定である」とされており、こちらの説明の方が適切であったと思います。
- どちらにしても、「固体の塩化銀のモル濃度は反応前後で変わらず、定数として扱うことができる」という点では変わりませんが。
したがって、K[AgCl(固)]をまとめて1つの定数Kspとすると、Ksp=[Ag+][Cl-]となります。そして、このKspのことを溶解度積と呼んでいます。
溶解度積は温度にのみ依存する
溶解度積において最も重要なことは、温度を変えない限り溶解度積は一定であるということです。
なぜ温度を変えない限り一定になるのかというと、「平衡定数は温度を変えない限り一定となる」というのが化学平衡の法則だからです。
そのため溶解平衡の計算問題の解法の方針は、溶解平衡であると判断できたら、Kspつまり溶解度積が一定となるということを使って方程式を立てるというのが基本の方針となります。
溶解平衡になっているか(沈殿が生じているか)の判断方法
ここで1つポイントがあります。Ksp=一定となるのは、溶解平衡となっているときなのですが、ではどのように溶解平衡になっているかを判断すればよいのでしょうか。
それは、沈殿が生じたときです。沈殿が生じたら、その水溶液は溶解平衡になっていると判断することができます。なぜなら沈殿の表面で溶解と析出が絶えず行われるからです。
沈殿が生じるか否かの判断方法
では今度は、沈殿が生じるか否かの判断をどのようにするかを確認します。
沈殿が生じるか否かを判断したい場合は、まず全てイオンとなった(溶解した)と仮定します。
例えば、塩化銀であれば塩化銀の沈殿は生じず、塩化銀は全て銀イオンと塩化物イオンになったと仮定します。
溶解度積Kspよりも小さいとき
そして、その銀イオンのモル濃度と塩化物イオンのモル濃度を計算して、それらをかけてみてKspつまり溶解度積よりも小さくなったら、沈殿は生じていないと判断することができます。
Kspに達していないということは、まだ溶解平衡に達していないということであり、このイオンの積がKspになるまでまだイオンが溶ける余地があるということになります。
溶解度積Kspよりも大きいとき
そして次に、塩化銀は全て銀イオンと塩化物イオンとなり、銀イオンのモル濃度と塩化物イオンのモル濃度を計算し、それらの積を求めてみたとき、Kspを超えてしまったら、それは沈殿が生じているということになります。
なぜなら、溶質のイオンの積がKspつまり溶解度積を超えるということは、ありえないからです。それは矛盾しているので、全てイオンとなって溶解しているという仮定が間違っているのであり、つまり実際は全てイオンとなったわけではなく、沈殿しているものがあるということになります。
溶媒に何かを溶かしたときは、Kspを超えないように沈殿が生成します。例えば、銀イオンや塩化物イオンを溶かしてKspを超えそうになったら、Kspを超えないように塩化銀が析出して、銀イオンと塩化物イオンのモル濃度を小さくします。
したがって、Kspつまり溶解度積は、溶かすことができるイオンの限界を示していると考えることもできます。つまり、Kspを超えないのであれば水溶液にイオンを溶かしておけますが、Kspを超える量のイオンを水溶液に溶かしておくことはできないということになります。
- 気液平衡かどうか(液体の水が存在するか)の判断方法と似ています→気体の燃焼(閉鎖系)の計算(気液平衡とは何か、飽和蒸気圧の使い方、液体が存在するかどうかの判断の方法についても解説しています)
ここまでが溶解平衡あるいは溶解度積の基本的な考え方です。
問題演習①(溶解度積を使った計算)
それではこの問題を解きます。
Ksp=[Ag+][Cl-]=8.1×10-11(mol/L)2である。AgClは水1.0Lに最大で何g溶けるか。ただし Ag=108、Cl=35.5とし、有効数字は2桁で答えます。
「最大で何g溶けるか」は、「溶解平衡に達したときに塩化銀はどれだけイオンとなって溶けているか」と考えます。
それでは答案を確認していきます。
まずは求める溶けた塩化銀の質量をw(g)とします。そして、溶解平衡つまり平衡状態を考えるので、反応前、変化量、反応後の表を作ります。今回この表の単位はmolとします。

まず反応前ですが、塩化銀を多量とします。なぜ多量とするかというと溶解平衡となっているということは、沈殿が形成されているということだからです。そして、反応前なので銀イオンと塩化物イオンは0です。次に変化量ですが、今回は溶けた塩化銀の質量をwとしているのでそれをmolにするために、塩化銀のモル質量で溶けた塩化銀の質量を割ることで、溶けた塩化銀の物質量とします。そのため塩化銀の変化量は、-w/143.5となります。そして、化学反応式の係数の比が1:1:1なので、右辺の銀イオンと塩化物イオンの変化量は共に+w/143.5となります。よって、溶解平衡に達した後は、反応前と変化量を足すのですが、結晶となって沈殿している塩化銀は変化しないものとして、溶解平衡に達した後水溶液に溶けている銀イオンの物質量はw/143.5となり、同様に溶けている塩化物イオンの物質量もw/143.5molとなります。
したがって、温度を変えない限り溶解度積は一定となるので、この溶解平衡のときの溶解度積も8.1×10-11となります。ここで注意したいのが、溶解度積はモル濃度の積なので、単位がmol/Lとなるように物質量を体積で割るのを忘れないようにしましょう。
あとは、この方程式を解きます。今回は計算は省略して、w=1291.5×10−6≒1.3×10-13となります。
1つだけ計算のポイントをいうと、8.1×10-11は81×10-12とすると、81は9の2乗なのでwの2乗を外すことができるようになります。
いかがでしょうか。これが溶解平衡となっているときの基本的な計算の流れとなります。
問題演習②(沈殿が生じるか否かの判断)
それでは次は沈殿が生じるか否かを判断する問題を解きます。
先ほどの問題と同じ温度で、Ksp=[Ag+][Cl-]=8.1×10-11(mol/L)2であるとし、0.10mol/LのAgNO3水溶液100mLに0.10mol/LのNaCl水溶液を0.20mL加えたとき、AgClの沈殿は生じるかどうか考えてみます。
それでは答案を作っていきます。
まずは仮定する
まずは、Ag+とCl-が全て塩化銀の沈殿は形成せずに水溶液中でイオンになっていると仮定します。
そして次に、硝酸銀と塩化ナトリウムの電離の反応式
硝酸銀の電離:AgNO3 → Ag++NO3-
塩化ナトリウムの電離:NaCl → Na++Cl-
を確認します。これらは難溶性の塩ではないので、水溶液中で100%電離してそれぞれイオンとなります。
銀イオンのモル濃度を求める
そのため、この仮定のもとで銀イオンのモル濃度は、以下のように求めることができます。
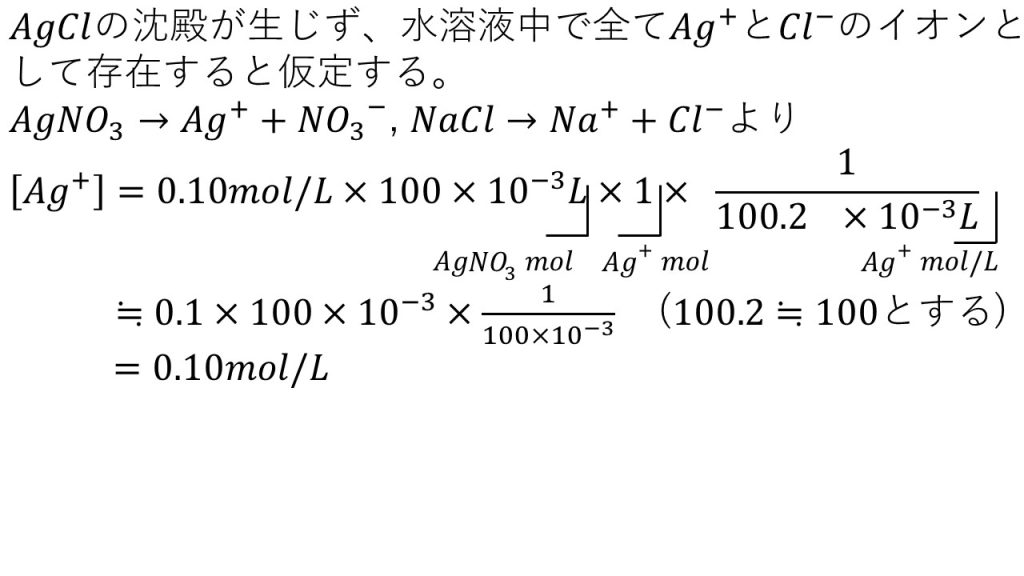
硝酸銀水溶液のモル濃度に溶液の体積をLにしたものをかけることで、溶質である硝酸銀の物質量となります。そして、硝酸銀の電離の化学反応式の係数の比が1:1:1なので、×1をすることで、銀イオンの物質量となります。さらに今回は2つの水溶液を混ぜるので、混ぜた後の体積で割ることで、混ぜた後の銀イオンのモル濃度となります。
それでは、この式を計算していくのですが、100.2は100と近似すると計算が楽になります。100.2で割るのも100で割るのも計算結果に大きな変化はないので、このように近似しても構いません。
あとは計算すると、この「Ag+とCl-が全て塩化銀の沈殿は形成せずに水溶液中でイオンになっている」という仮定のもとで、混ぜた後の銀イオンのモル濃度は0.10mol/Lとなります。
塩化物イオンのモル濃度を求める
同様にして 塩化物イオンのモル濃度を求めると、式は以下のようになります。
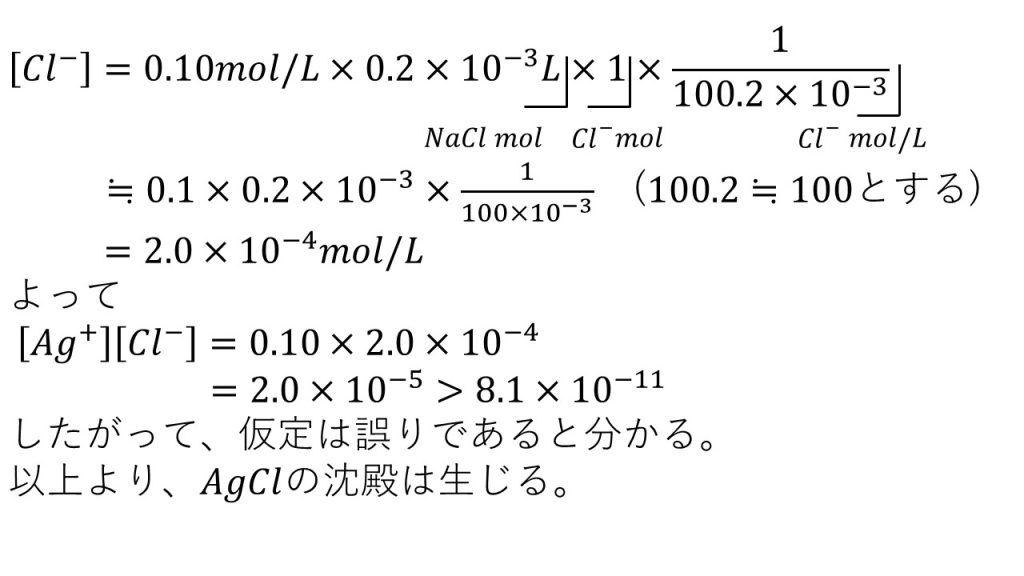
どちらも注意したいのは、混ぜた後のモル濃度を求めるようにしましょう。混ぜる前のモル濃度を使って計算してしまうと、間違えてしまうので注意してください。
仮定のもとでのモル濃度の積と溶解度積を比べる
それでは、「塩化銀の沈殿は生じず銀イオンと塩化物イオンが全てイオンになっている」という仮定のもとで銀イオンと塩化物イオンのモル濃度を求めることができたので、あとはこれらをかけると2.0×10-5となり、これは塩化銀の溶解度積である8.1×10-11を大きく上回っています。
よって、溶解しているイオンの積が溶解度積を超えるということはありえないので、この沈殿が生じないという仮定は誤りであるということが分かります。
したがって、塩化銀の沈殿は生じると判断することができます。
いかがだったでしょうか。溶解平衡あるいは溶解度積の問題の解法の流れが理解できたでしょうか。ぜひ復習しておいてください。
- 溶解平衡(溶解度積)の計算の応用問題(共通イオン効果)→共通イオン効果を扱った問題の解説(共通イオン効果とは何か、図を使った問題の解説もしています)
(3)解説授業の内容を復習しよう
(4)溶解平衡(溶解度積)の解説一覧
①溶解平衡(溶解度積)の計算(溶解平衡とは何か、溶解度積=一定の導出、沈殿が生じるかどうかの判断の方法についても解説しています)
②共通イオン効果を扱った問題の解説(共通イオン効果とは何か、図を使った問題の解説もしています)
(5)参考
☆化学の解説動画・授業動画一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識テスト一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の解説・授業・知識・演習問題一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の語呂合わせ(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
「化学計算の王道」シリーズは『思考訓練の場としての体系化学』(GHS予備校)を参考にしています。
GHS予備校についてはこちら→https://ghs-yobikou.co.jp/
思考訓練シリーズの購入はこちら→https://ghs-yobikou.shop/
