(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
根号や虚数単位iを代入して式の値を求める問題の解法
根号や虚数単位iを代入して式の値を求めるタイプの問題は2つのステップで解きます。
まずは、①根号(ルート)や虚数単位iをなくします。
そして、②式の次数下げを行います。
例題1:根号を代入して式の値を求める問題
具体的に問題を解きながら、この解法を確認してみます。
【問題】
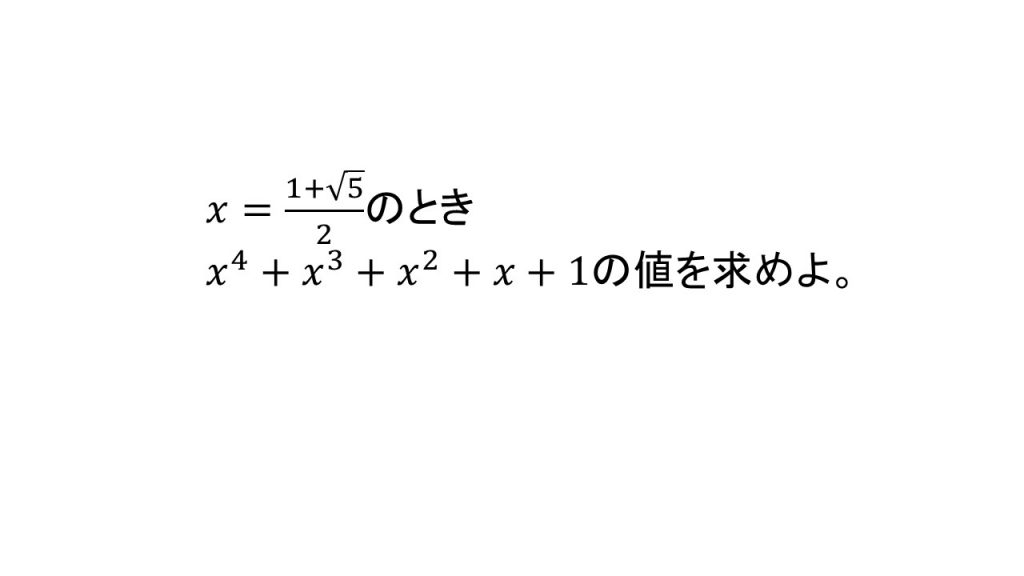
【答え】

【解説】
-1024x576.jpg)
(ア)をそのままx4+x3+x2+x+1に代入して計算して式の値を求めることもできます。しかし、それはとても面倒ですし、計算ミスをしてしまう可能性も大きいです。そのため、こういった問題を簡単に解くために
①根号(ルート)や虚数単位iをなくす
②式の次数下げ
この流れで解いてみます。
①根号(ルート)をなくす
まずはルートをなくしてみます。
やり方としては、右辺に√だけになるように式変形をして、両辺を2乗します。そうすることで、√がなくなります。
あとは、この式を整理したx2-x-1=0を使って、式の値を求めます。ここまでが、1つ目のステップとなります。
②式の次数下げ
次に、この式を使って、次数下げを行います。
イメージとしては、値を求める式をx2-x-1を使って表してみます。1番簡単なやり方は、割り算をすることなのですが、まだ習っていない人のためにまずは割り算を使わないで次数下げをする方法をご紹介します。
x4をx2-x-1を使って表してみます。このようにx2(x2-x-1)とすれば、x4ができます。あとはイコールが成り立つようにつじつまを合わせていきます。x2×(-x)で-x3となるので、+2x3を加えます。そして、x2×(-1)で-x2となるので、+2x2を加えます。そして、残りはそのまま書きます。これで、x4の次数下げが出来ました。
次に、この2x3の次数下げを行います。先ほどと同様に、2x(x2-x-1)とすることで、2x×x2=2x3となるので、この2x3をx2-x-1で表すことが出来ます。あとは、先ほどと同様につじつまを合わせていきます。2x×(-x)で-2x2となるので+4x2を加え、2x×(-1) で-2xとなるので+3xを加え、残りはそのまま書くと、つじつまが合います。
そして最後に、4x2をx2-x-1を で表すために、4(x2-x-1)とします。こうすることで、4×x2=4x2となり、あとはつじつまを合わせていきます。 4×(-x)で-4xとなので+7xを加え、4×(-1)で-4となので+5を加えることで、つじつまが合います。
このように、次数が高い順番で、x2-x-1で表すことで次数下げができます。式変形のポイントとしては、常に元に戻るか確認しながら式変形をするとよいです。
次数下げをした式にx2-x-1=0を代入する
そして次数下げが終わったら、あとは(ア)を、x4+x3+x2+x+1に代入していきます。(ア)を式変形してx2-x-1=0を導いたので、x2-x-1に(ア)を代入すると0となります。
このことを利用して、式の値を求めてみると、x2( x2-x-1)に(ア)を代入すると0になり、2x(x2-x-1)も0になり、4(x2-x-1)も0になり、残ったのは7x+5なので、これに(ア)を代入して、計算して整理すると答えが出ます。
このように、そのままやろうとすると4乗や3乗や2乗をしないといけないところを、うまく式変形することで、4乗も3乗も2乗も計算しなくてよくなり、計算しなければいけない次数が下がるので、次数下げというわけです。
割り算で次数下げをする方法
また、割り算をして次数下げをする方法も確認します。

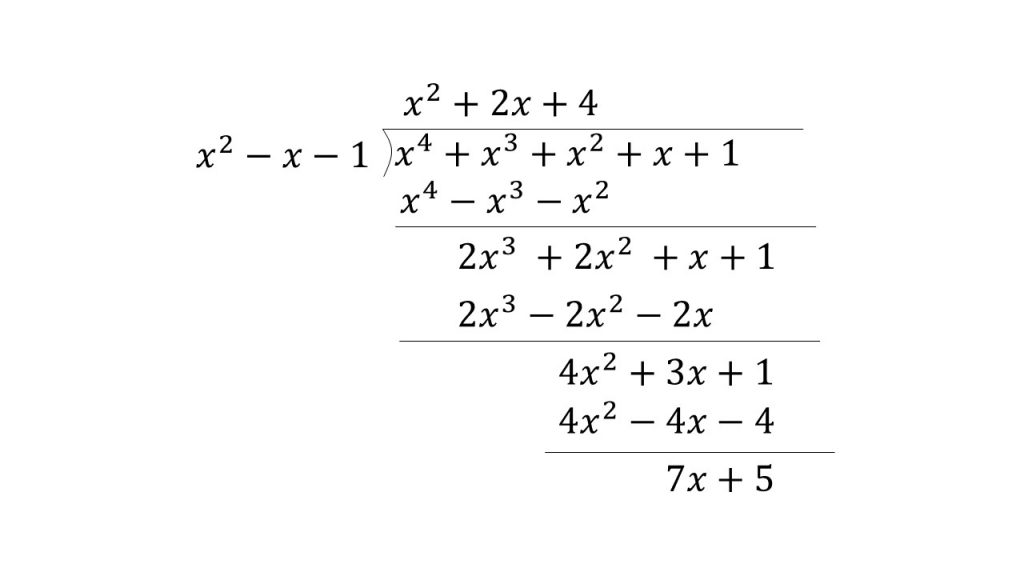
x4+x3+x2+x+1をx2-x-1で割ります。すると、商がx2+2x+4となり、余りが7x+5となります。このように、商と余りが出れば、
(割られる数)=(割る数)×商+余り
の関係を使って元の式を、
(x4+x3+x2+x+1)=(x2-x-1)(x2+2x+4)+7x+5
のようにx2-x-1で表すことが出来ます。あとは先ほどと同様に、(ア)を代入してみると、(x2-x-1)(x2+2x+4)が0になり、結局7x+5に(ア)を代入して計算すればよいということになります。
このように、整式の割り算を習っている場合は、割り算を使って次数下げをするようにしましょう。
例題2:虚数単位iを代入して式の値を求める問題
それでは次に、虚数単位iを代入して、式の値を求める問題を解いてみましょう。
【問題】

【答え】


【解説】
-1024x576.jpg)
①根号(ルート)や虚数単位iをなくす
先ほどと同様に、最初に√やiをなくしていきます。
そのために、√2iだけを右辺に残します。そして両辺を2乗して、√とiをなくします。i の2乗は-1になるので計算ミスをしないように注意してください。
そして、整理するとx2-2x+3=0になります。
②式の次数下げ
次に、このx2-2x+3=0を使って次数下げをしていきます。今回は、割り算で次数下げをします。
値を求める式を、先ほど作ったx2-2x+3で割ると、商はx2-2x-5となり、余りは2x+10となります。よって、
(割られる数)=(割る数)×商+余り
の関係から、
x4-4x3+2x2+6x-5=(x2-2x+3)(x2-2x-5)+2x+10
このように式変形ができます。
次数下げをした式にx2-2x+3=0を代入する
最後に、この式に(イ)を代入します。
x2-2x+3に(イ)を代入すると0となるので、(x2-2x+3)(x2-2x-5)が丸ごと0となり、2x+10に(イ)を代入して、計算して整理すると答えとなります。
このように、
①根号つまりルートや虚数単位iをなくす
②式の次数下げ
この手順で解くと、4乗・3乗・2乗を計算する必要がなくなり、ラクに正確に式の値を求めることができます。
(3)解説授業の内容を復習しよう
②高次式の値(代入する値に虚数単位iを含む場合、次数下げを利用)
(4)実数(数学Ⅰ)の解説一覧
①数の分類一覧(複素数、実数、有理数、無理数、整数、自然数、素数)
②根号(ルート)の中に2乗があるときの対処法(根号(ルート)は「正の平方根」という意味です)
④根号や虚数単位iを含む式を代入して式の値を求める問題の解法(次数下げ)
※虚数を習っていない場合は、後半を飛ばしてください。
⑤数学で守らないといけないルール(文字で割るときの注意点、係数に文字を含む方程式の解法、係数に文字を含む不等式の解法)
(5)複素数と方程式(数学Ⅱ)の解説一覧
①解と係数の関係の証明(三次方程式の解と係数の関係も解説しています)
②高次式の因数分解・高次方程式の解法の解説(因数定理を正確に理解しよう!)
③根号や虚数単位iを含む式を代入して式の値を求める問題の解法(次数下げ)
④1の3乗根ω(オメガ)とは何か(ωの意味と使い方についての解説)
