(1)問題

(2015年度センター試験本試数学ⅡB第3問より)
(2)答案
☆動画による解説はこちら→数列を理解できているか試すことができる良問の解説(2015年センター試験本試数学ⅡB第3問を記述問題に改題しています)

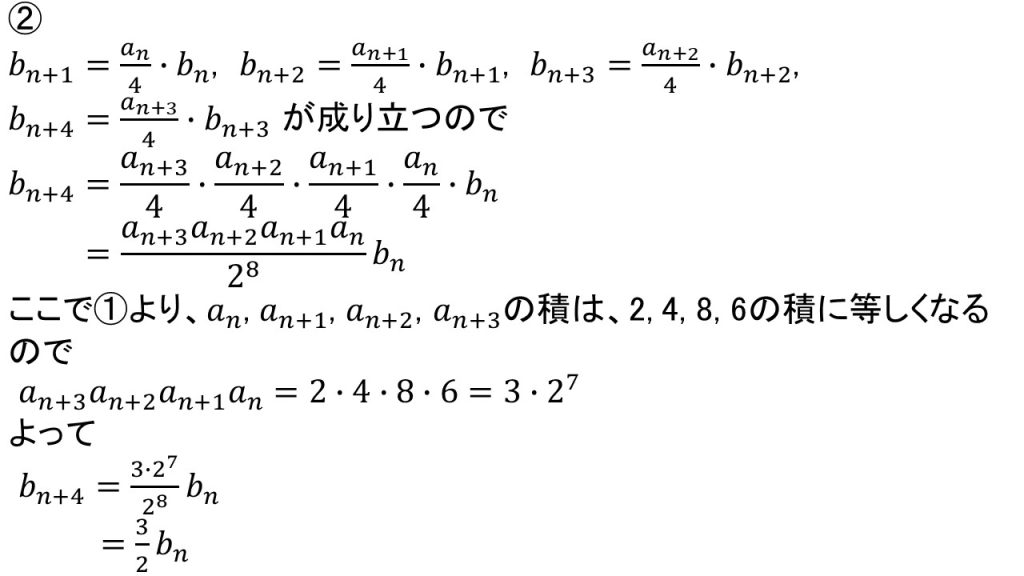


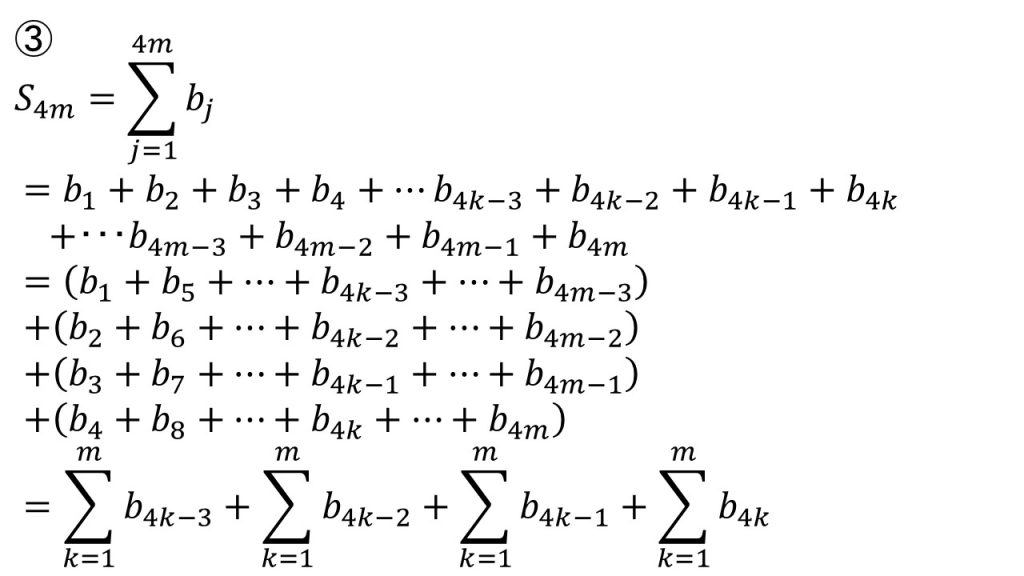
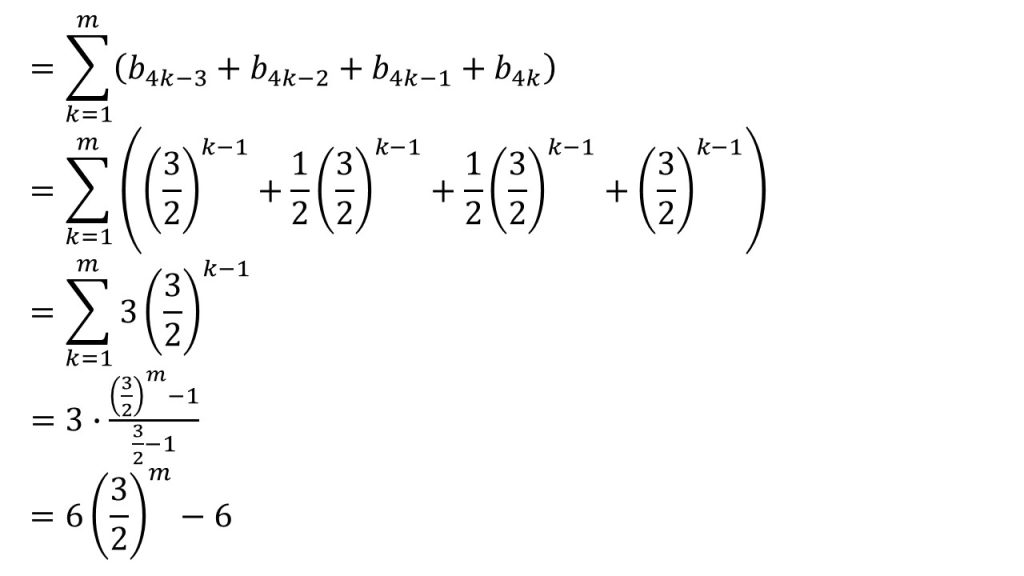
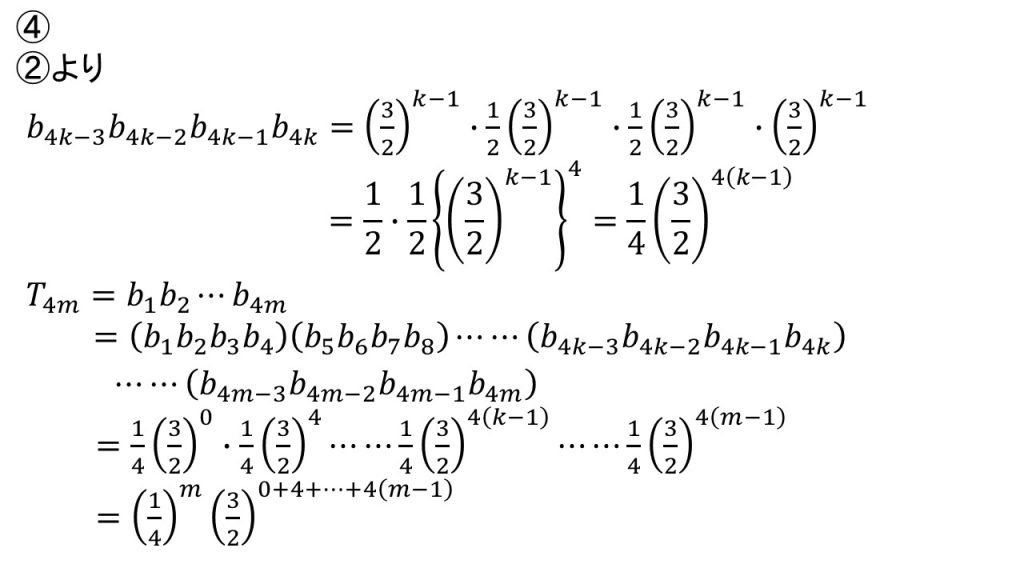

(3)解法のポイント
☆詳しい解説はこちら→数列を理解できているか試すことができる良問の解説(2015年センター試験本試数学ⅡB第3問を記述問題に改題しています)
数列の原理が正しく理解できているかを問う良問です。この問題が、できるようになったら数列はマスターしたといってもいいでしょう。
①余りは周期性を持つということは知っておきましょう。今回は一の位の数、つまり10で割った余りなので、周期性を持ちます。
数列に限らず、数学で周期性は重要なキーワードになることが多いです。見落とさないようにしましょう。
②bn+4とbnの関係式を作るなど、項数が飛んでいる場合は、間の項を順番に代入して、間を埋めるという操作をすることは知っておきましょう。
また、②の後半は、b1, b2, b3, b4の間には簡単な関係はないが、b1, b5, b9……の間には等比数列の関係があるということに気付けるかがポイントです。
このように、隣り合っている項の間の関係性が見つからないときは、飛んだ場所にある項との関係を考えてみるとよいです。
③Σの問題でよく分からなくなったら、とりあえず具体的に数列を書いてみるとよいです。
今回は、②で4つ先の項とは等比数列の関係になっていることが分かっているので、等比数列の関係になっているものでまとめます。
今回みたいにΣの上がnやmではなく、4nや4mになっていたら、「4つのセットを作って考えよう」というサインです。見落とさないようにしましょう。
④積の場合も③と同様に、具体的に書いてみて、関係があるセットでまとめます。
今回は、4つのかたまりをmセット作ることで解くことができます。
☆詳しい解説はこちら→数列を理解できているか試すことができる良問の解説(2015年センター試験本試数学ⅡB第3問を記述問題に改題しています)
(4)必要な知識
①等差数列


②等比数列

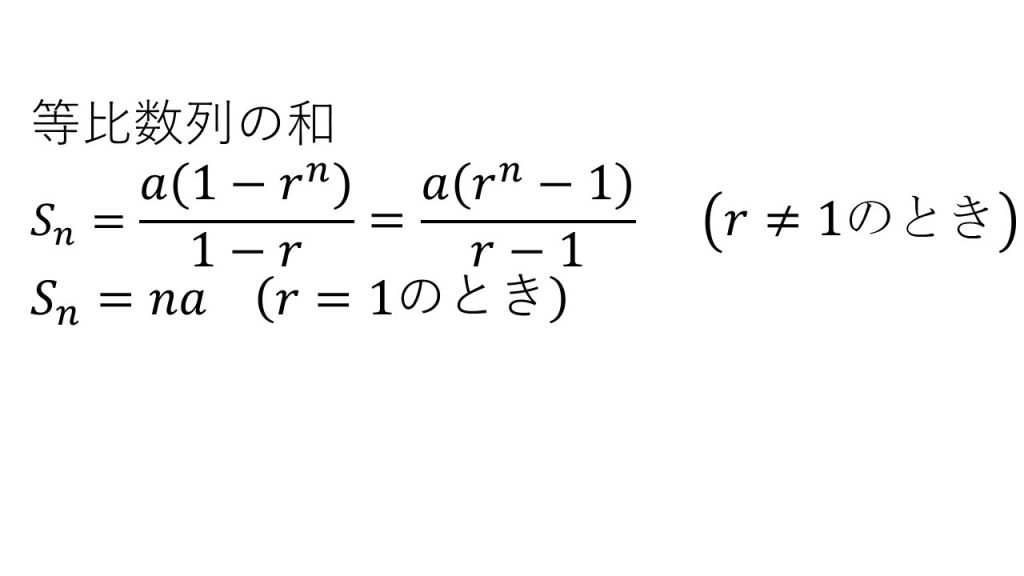
③Σの定義
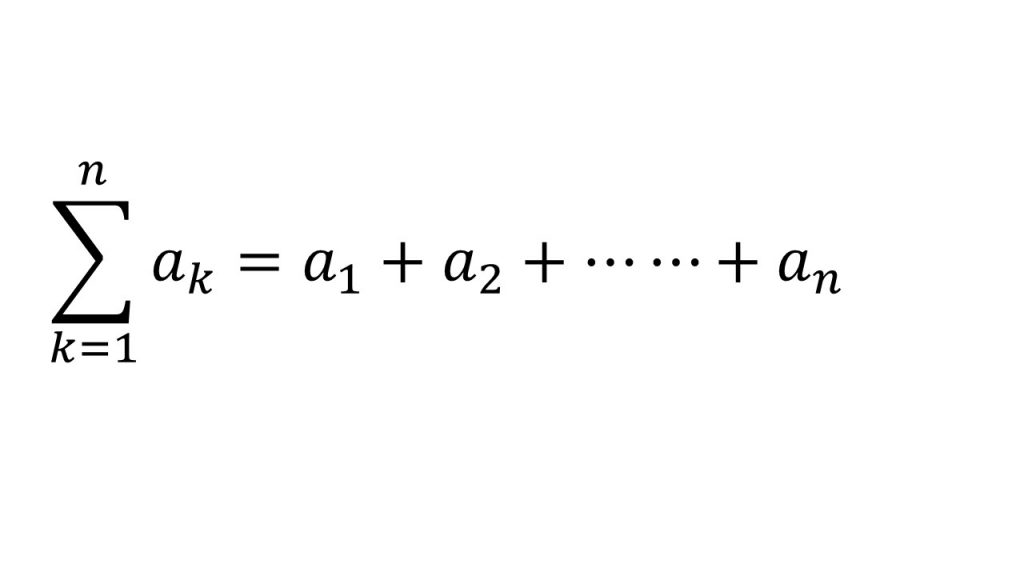
①指数法則
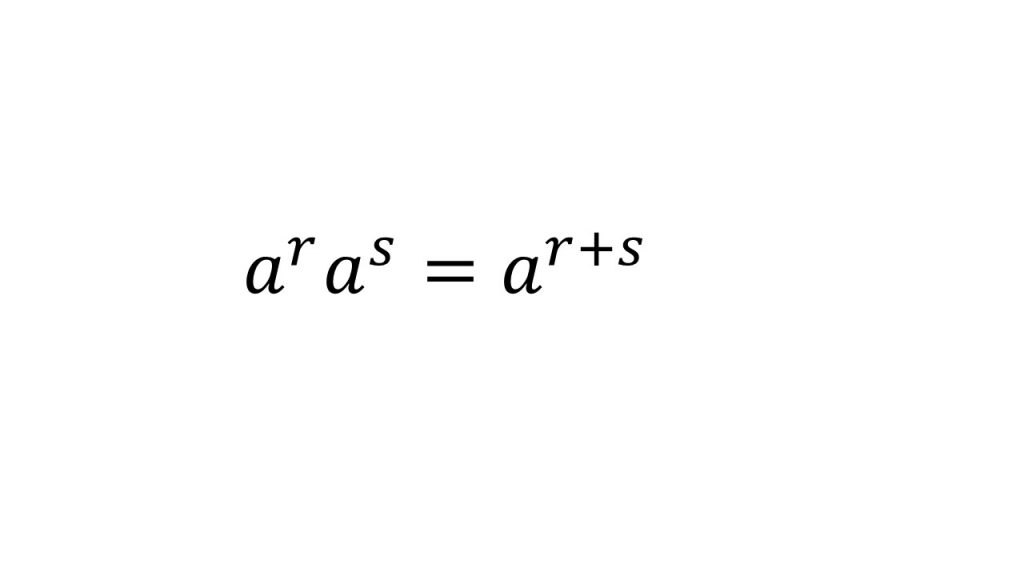
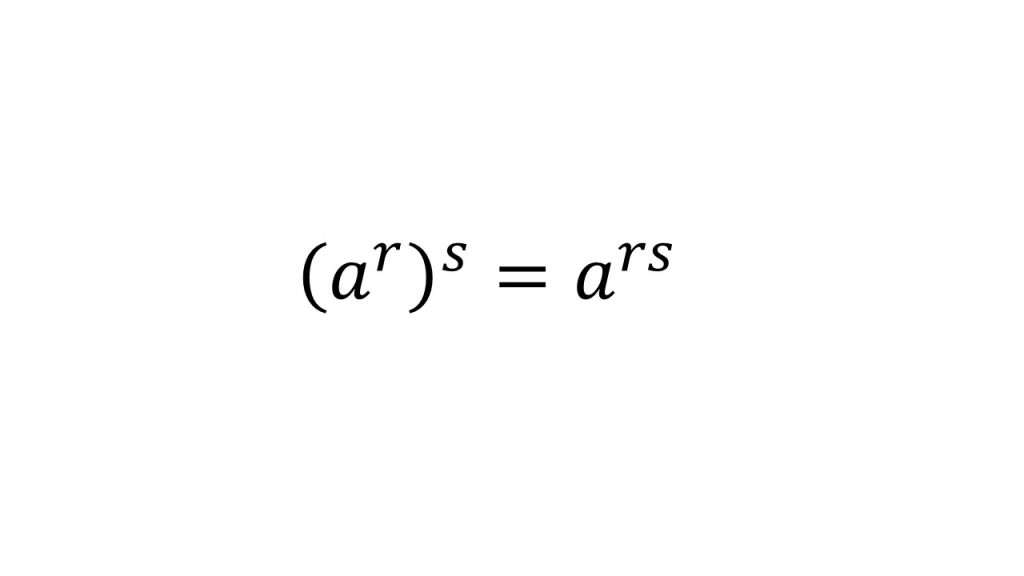
(5)動画による解説
①数列を理解できているか試すことができる良問の解説(2015年センター試験本試数学ⅡB第3問を記述問題に改題しています)
