数列を理解できているか試すことができる良問の解説（2015年センター試験本試数学ⅡB第3問を記述問題に改題しています）

（１）解説授業動画

（２）解説授業の原稿

数列を理解できているかどうかを試すことができる良問

今回は2015年センター試験本試験数学ⅡB第3問（数列）の解説をします。

この問題は数列が理解できているかどうかを試すことができるとても良い問題です。ぜひ数列の学習の仕上げとして解いてみてください。

なおセンター試験なので本来はマーク式の問題ですが、今回は記述問題として改題してあるのでご注意ください。

問題の確認

それでは、問題を確認します。

※問1の[オ]はn以外のnを使った式を答える。

問1の解説

それでは、まずは問1を解きます。

a₂, a₃, a₄, a₅は、実際に2ⁿのnに2, 3, 4, 5を代入してみて、その一の位を確認してみます。このように数列の問題は、実際にいくつか代入してみて、法則や周期性を探すところから始めることが多いです。

そして、a_[オ]=a_nの等式が何を表しているかというと、{a_n}という数列は周期性があるということを表しています。なぜなら、ある項の数字と同じ数字が、別の場所に周期的に現れるということを表しているからです。

それでは、問1の答案を確認します。

先ほども確認した通り、2ⁿのnにどんどん値を代入していきます。2¹=2なので一の位は2となり、2²=4なので一の位は4となり、2³=8なので一の位は8となり、2⁴=16なので一の位は6となり、2⁵=32なので一の位は2となります。そして、ここでa₁と同じ値が出てきました。こうなると周期性が見えてきます。実際に代入して確認してみてもいいのですが、a₆=4, a₇=8, a₈=6, a₉=2となります。

このように実際に代入していくと、{a_n}という数列は、2, 4, 8, 6, 2, 4, 8, 6, 2, 4, 8, 6……のように2, 4, 8, 6を繰り返す数列であるという周期性が見つかります。

よって、例えばa_n=2とすれば、次に2になるのは4つ後なので、a_n+4=a_nが成り立つと考えることができます。

余りには周期性がある

一の位の数というのは、10で割った余りということなのですが、余りというものには周期性があるということは数学において非常に重要なので、余りが絡む問題を解くときは必ず意識しましょう。今回で言えば、2ⁿを10で割った余りは、2, 4, 8, 6を繰り返しています。

ちなみに、この答案をちゃんと記述すると以下のようになります。

2ⁿ⁺¹=2・2ⁿなので、2ⁿ⁺¹を10で割った余りa_n+1は、2ⁿを10で割った余りa_nに2をかけたものの一の位に等しいということが分かるので、数列{a_n}は、2, 4, 8, 6を繰り返す数列である。したがって、すべての自然nに対して、a_n+4=a_nが成り立つ。

といった答案になります。

「2ⁿ⁺¹を10で割った余りa_n+1は、2ⁿを10で割った余りa_nに2をかけたものの一の位に等しい」の部分が言っていることを具体的に確認すると、a₁=2のとき、a₂は2の2倍をしたもの（つまり4）となり、a₃はa₂の2倍をしたもの（つまり8）となり、a₄はa₃の2倍をしたもの（つまり16）の一の位である6となり、a₅はa₄の2倍をしたもの（つまり12）の一の位の2となります。そして、ここでa₁と同じ2が出てきたので、以降はまったく同じことが繰り返されるといことを表しています。

問2前半の解説

それでは次は問2を解きます。

まずは、問2の前半の問題を確認します。b_n+4をb_nを使って表します。

この問題をどのように考えればよいかというと、とりあえず、まずb_n+4を作ってみようと考えてみます。そして、与えられている式を確認するとb_nを使った式は、b_n+1=a_nb_n/4しかありません。そのため、この式を使ってb_n+4を作るために、このnにn+3を代入してみます。すると、b_n+4=a_n+3b_n+3/4となります。こうなると、b_n+4を知るためにはb_n+3が必要であると分かります。

そこで、b_n+3でも同様のことをしてみると、b_n+3を知るためにはb_n+2が必要ということが分かります。次にb_n+2で同様のことをしてみると、b_n+2を知るためにはb_n+1が必要であるということが分かります。

そして、この元の式b_n+1=a_nb_n/4を見てみると、b_n+1はb_nで表されています。つまり、このようにたどってみるとb_n+4とb_nをつなげることができそうです。

これが発想のポイントとなります。

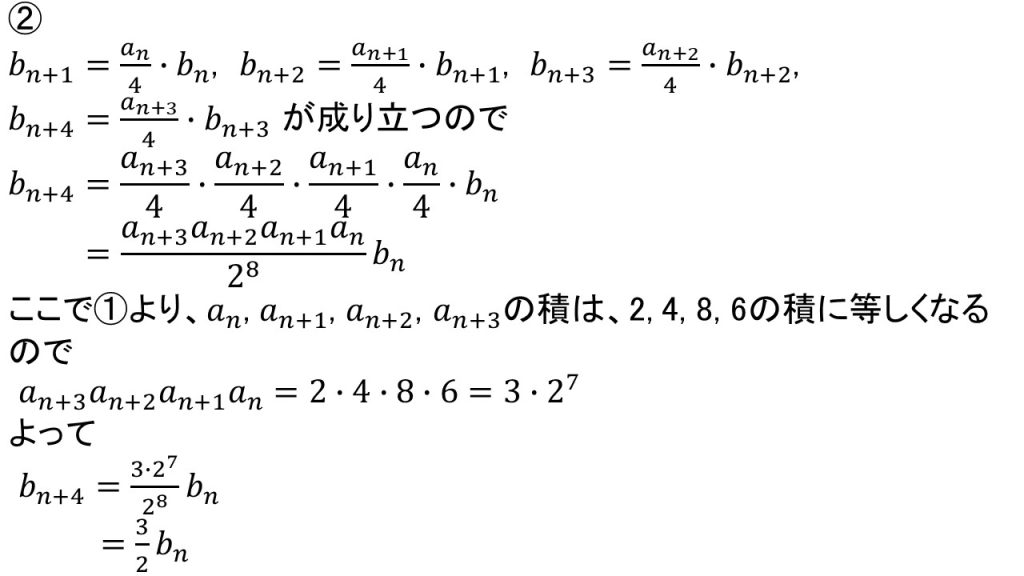
これが問2の前半の答案です。

b_n+1=a_n/4・b_nはもともと与えられている式です。この式のnにn+1を代入すると、b_n+2=a_n+1/4・b_n+1となり、この元の式のnにn+2を代入すると、b_n+3=a_n+2/4・b_n+2となり、この元の式のnにn+3を代入すると、b_n+4=a_n+3/4・b_n+3となるので、このb_n+4=a_n+3/4・b_n+3にb_n+3=a_n+2/4・b_n+2を代入し、さらにb_n+2=a_n+1/4・b_n+1を代入し、そしてb_n+1=a_n/4・b_nを代入すると、

b_n+4=a_n+3/4・a_n+2/4・a_n+1/4・a_n/4・b_n

となります。4=2²なので分母を整理すると、

b_n+4=a_n+3a_n+2a_n+1a_n/2⁸・b_n

となります。ここで問1より、a_n, a_n+1, a_n+2, a_n+3の積は2, 4, 8, 6の積に等しくなります。なぜなら、{a_n}は2, 4, 8, 6が繰り返される数列だからです。つまり、数列{a_n}のうちから連続する4つの項を取り出せば、必ず2, 4, 8, 6が1つずつ含まれています。例えば、a_n=2であればa_n+1=4, a_n+2=8, a_n+3=6となり、a_n=4であればa_n+1=8, a_n+2=6, a_n+3=2となり、a_n=8であればa_n+1=6, a_n+2=2, a_n+3=4となるように、順番がどうなるにせよ、a_n, a_n+1, a_n+2, a_n+3の積は、2・4・8・6と等しくなります。

よって、それをb_n+4=a_n+3a_n+2a_n+1a_n/2⁸・b_nに代入して約分すると、答えはb_n+4=3/2・b_nとなります。

計算のポイント

ここでの計算のポイントは、2⁸や2⁷を計算してしまわない、ということです。

こういったものは計算せずに、素因数分解の形で取っておくと、約分がしやすくなり、ラクに計算ができます。

b_n+4=3/2・b_nが意味すること

そして、ここで答えを出して終わり、としないようにしましょう。答えの式の意味を考えてみます。

b_n+4=3/2・b_n

この式は、「b_n+4はb_nに3/2をかけたものである」ということを表しています。つまり、「b_n+4とb_nは等比数列の関係になっている」ということをこの式は表しているのです。

このように、数列や漸化式の問題を解くときは、式の意味を言葉で表してみると、解決の糸口となることが多いです。それでは、このことに注意しながら、問2の後半の問題を確認してみます。

問2後半の解説

それでは、問2の後半の問題を確認します。

b_4k－3, b_4k－2, b_4k－1, b_4kを求めます。

数列の問題で、まず何をすればよいか迷ったら、とりあえず1, 2, 3など具体的に値を代入してみて、法則や規則性を探してみます。

例えば、b_4k－3のkに1, 2, 3を代入してみると、b₁, b₅, b₉となり、{b_4k－3}が表す数列は、ある項と次の項の関係がb_nとb_n+4の関係になっているということに気がつきます。そして、問2の前半で、b_n+4=3/2・b_nつまりb_n+4とb_nは等比数列の関係になっていると求めていたので、{b_4k－3}が表す数列は等比数列であるということが分かります。

したがって、問2の後半の答案は以下のようになります。

{b_4k－3}が表す数列、つまり、b₁, b₅, b₉……b_4k－3は、初項がb₁で、公比が3/2の等比数列となるので、等比数列の一般項の公式である『初項×公比の項数－1乗』となり、b_4k－3=(3/2)^k－1となります。項数はkであるということに注意しましょう。

同様に、{b_4k－2}が表す数列、つまり、b₂, b₆, b₁₀……b_4k－2は、初項がb₂で、公比が3/2の等比数列となるので、等比数列の一般項の公式を使うと、b_4k－2=1/2・(3/2)^k－1となります。

さらに、{b_4k－1}が表す数列、つまり、b₃, b₇, b₁₁……b_4k－1は、初項がb₃で、公比が3/2の等比数列となるので、b_4k－1=1/2・(3/2)^k－1となります。

そして、{b_4k}が表す数列、つまり、b₄, b₈, b₁₂……b_4kは、初項がb₄で、公比が3/2の等比数列となるので、b_4k=(3/2)^k－1となります。

ちなみに、それぞれの初項となったb₂, b₃, b₄は、問題文で与えられているb_n+1=a_nb_n/4にn=1, 2, 3を代入して求めています。

問3の解説

それでは問3を解きます。

まずは問題を確認してみると、S_nをb_nの和としたとき、S_4mを求めてみましょう。

ポイントは、S_nではなくS_4mになっているということです。このように数列の問題で、項数が4mなどになっている場合は、「4つのグループに分けよ」ということを意味しています。このヒントに気がつけるかどうかが、問3が解けるかどうかの分かれ目となります。

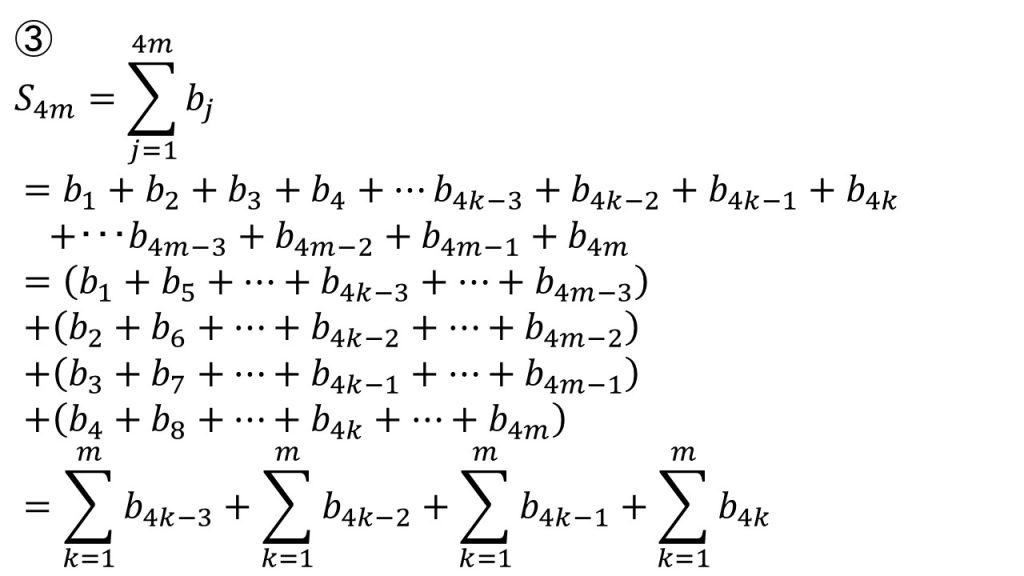
これが問3の答案の前半部分です。

S_4mはb_nのb₁からb_4mまでの和ということを表しています。

S_4m=b₁+b₂+b₃+b₄+……b_4k－3+b_4k－2+b_4k－1+b_4k+……+b_4m－3+b_4m－2+b_4m－1+b_4m

とにかく数列で分からなくなったら、このように具体的に書いてみましょう。そして、この和の式を、先ほど確認した「項数が4mになっているということは、4つのグループに分ける」という視点と、問2でb_nとb_n+4には等比数列の関係があるという2つの視点で、この式を見てみると、

S_4m=(b₁+b₅+……+b_4k－3+……+b_4m－3)
+(b₂+b₆+……+b_4k－2+……+b_4m－2)
+(b₃+b₇+……+b_4k－1+……+b_4m－1)
+(b₄+b₈+……+b_4k+……+b_4m)

このような4つのグループ分けをするということに気がつくことができます。つまり、(b₁+b₅+……+b_4k－3+……+b_4m－3)というグループと、(b₂+b₆+……+b_4k－2+……+b_4m－2)というグループと、(b₃+b₇+……+b_4k－1+……+b_4m－1)というグループと、(b₄+b₈+……+b_4k+……+b_4m)というグループの4つに分けます。

すると、それぞれのグループは問2でも確認した通り、等比数列となっています。よって、この1つ目のグループをΣで表したものは等比数列の和を表しいるということになり、2つ目のグループをΣで表したものも等比数列の和であり、3つ目のグループをΣで表したものも等比数列の和で、4つ目のグループをΣで表したものも等比数列の和となっています。

あとは、問2の後半でb_4k－3, b_4k－2, b_4k－1, b_4kの一般項は求めてあるので、それを代入して、それぞれのグループの和を求めて、それをすべて合計してもいいのですが、せっかくΣで表したので、Σの性質を使ってラクに速く計算するようにしましょう。

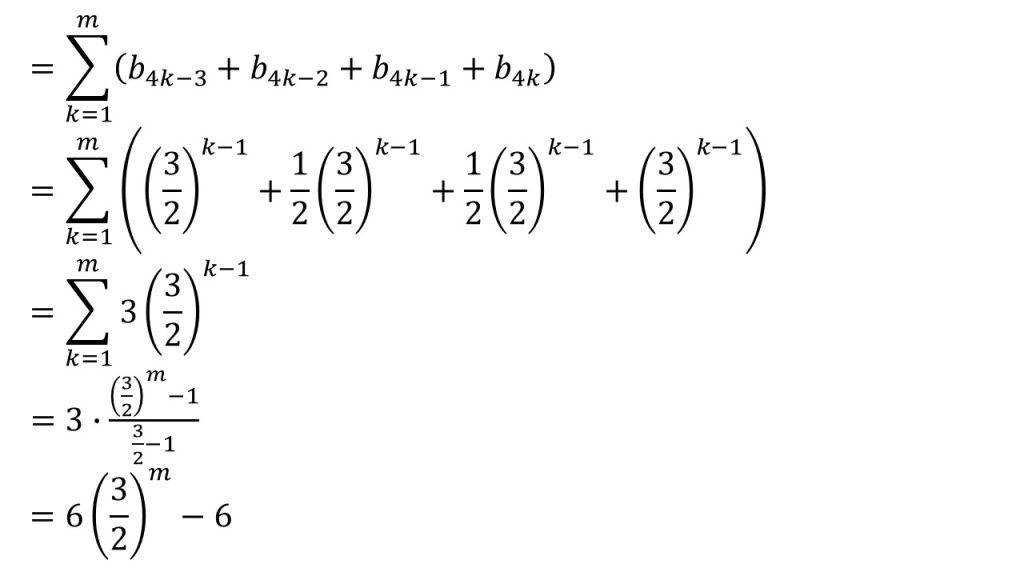
つまり、Σは分配法則が成り立つので、

Σ(b_4k－3+b_4k－2+b_4k－1+b_4k)

このように1つにまとめることができ、このようにまとめてからそれぞれを代入して、まずカッコの中を整理してから、Σの計算をして整理すると答えが出ます。

このようにすれば、それぞれでΣの公式を使う必要がなくなり、速くラクに計算することができます。

問4の解説

それでは、問4を解きます。

問4の前半はb_4k－3とb_4k－2とb_4k－1とb_4kの積を求めます。これは、それぞれの値は問2で求めているので、それぞれ代入して計算するだけです。そして後半はb₁からb_nまでの積をT_nと置いたとき、T_4mを求めてみます。

ここで問3のときに確認した通り、4mを見たら「まずは4つのグループに分けるのではないか」と考えてみましょう。

先に言うと、このT_4mを求めるときに4つのグループには分けないのですが、それでもグループ分けをするという発想は同じです。そのため、やはり数列の問題で項数が4mなどになっている場合は、まず4つのグループに分けるということを意識してみましょう。

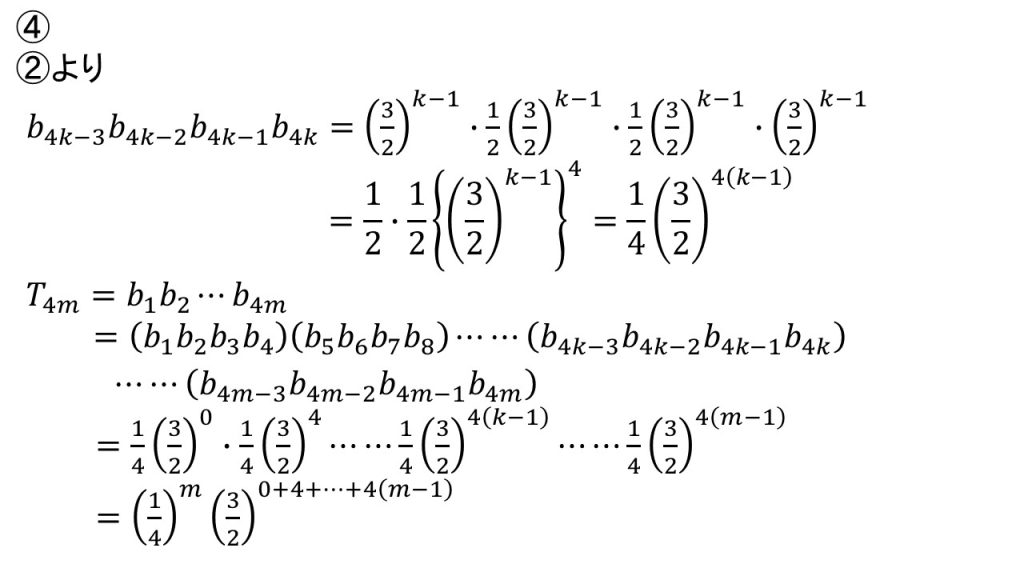
これが問4の答案の前半部分です。

まずはb_4k－3とb_4k－2とb_4k－1とb_4kの積を求めます。問2で求めたものをそれぞれ代入して計算をします。このとき指数の計算は指数法則を使うことに注意しましょう。(3/2)^k－1を4つかけているので、{(3/2)^k－1}⁴となり、指数法則により(3/2)^4(k－1)となります。

指数（数学Ⅱ）公式・指数法則一覧

b_4k－3とb_4k－2とb_4k－1とb_4kの積を求めるという誘導をヒントにしながら、T_4mを考えていきます。問3のときと同様にT_4mを具体的に考えてみます。

T_4mとはb₁からb_4mまでの積のことです。つまり、

T_4m=b₁・b₂・b₃・b₄・……・b_4m

となっており、この式をグループ分けをするという視点と、この前でb_4k－3とb_4k－2とb_4k－1とb_4kの積を求めているという2つの視点で見てみると、

T_4m=(b₁・b₂・b₃・b₄)・(b₅・b₆・b₇・b₈)……・(b_4k－3・b_4k－2・b_4k－1・b_4k)・……・(b_4m－3・b_4m－2・b_4m－1・b_4m)

このようなグループ分けをすればよいということに気がつきます。つまり、4つの積をmグループ作るということです。

このグループ分けをしたら、それぞれのグループを計算してみます。kグループ目の積は、1/2(3/2)^4(k－1)となるので、1グループ目の積は、この式のkに1を代入したものになり、2グループ目の積は、この式のkに2を代入したものになり、mグループ目の積は、この式のkにmを代入したものになります。

あとは、これを計算していきます。ここでもしっかり指数法則を使っていきます。まず、1/4がm回かけられているので、(1/4)^mとなります。そして、指数法則より、底が同じ指数のかけ算は、指数の足し算になります。よって、(3/2)^{0+4+8+……+4(m－1)}となります。

この指数の部分は、0, 4, 8, ……4(m－1)という数列の和になっています。