【考え方の基本】
- 分母の次数が分子の次数よりも大きいとき
- 分母の次数≦分子の次数のとき→次数下げ
- 置換積分法も検討してみる。
【例題】
☆問題のみはこちら→分数式の積分(問題)
①
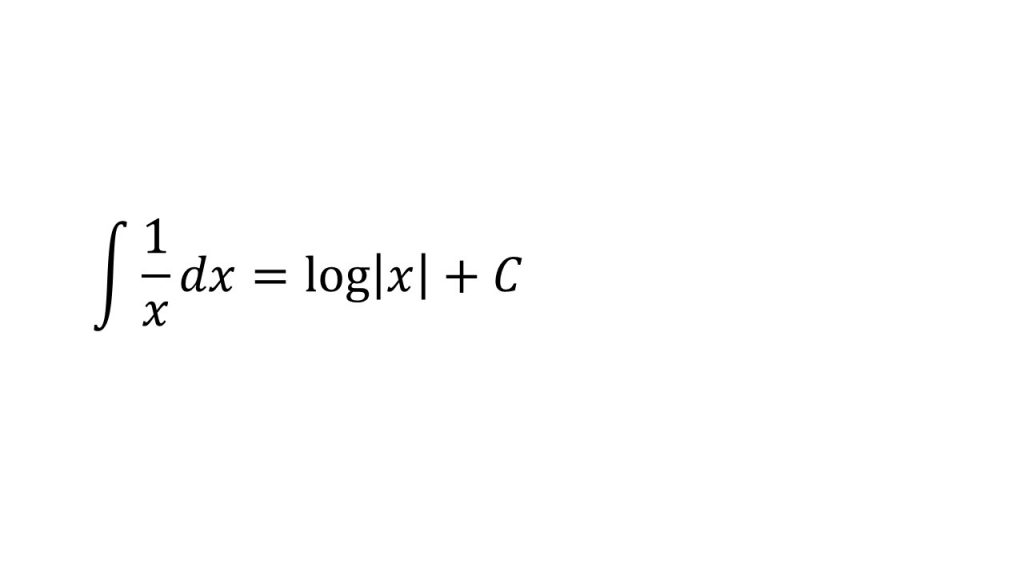
- 公式の利用→積分法(数学Ⅲ)公式
- 「積分は微分の逆である」ということも意識しよう。この問題であれば、対数関数の微分の逆をしている→「積分は微分の逆である」ということを意識して積分の公式を理解しよう!
②
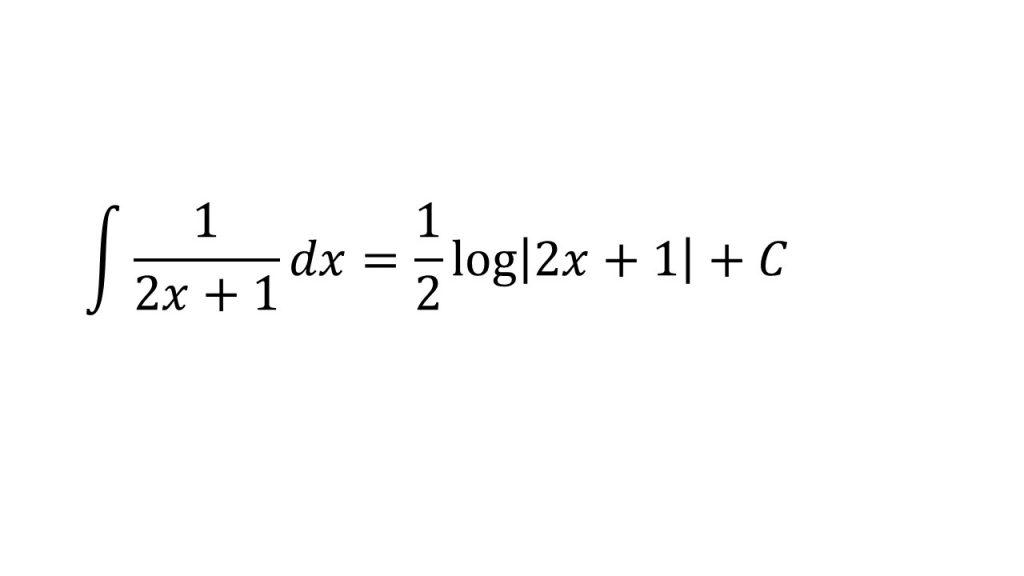
- 1/(2x+1)が合成関数となっていることに注意。
- 全体を積分(f(g(x))のf(u)をuで積分)した後、中身の微分(f(g(x))のg(x)をxで微分)の逆数をかける。
③
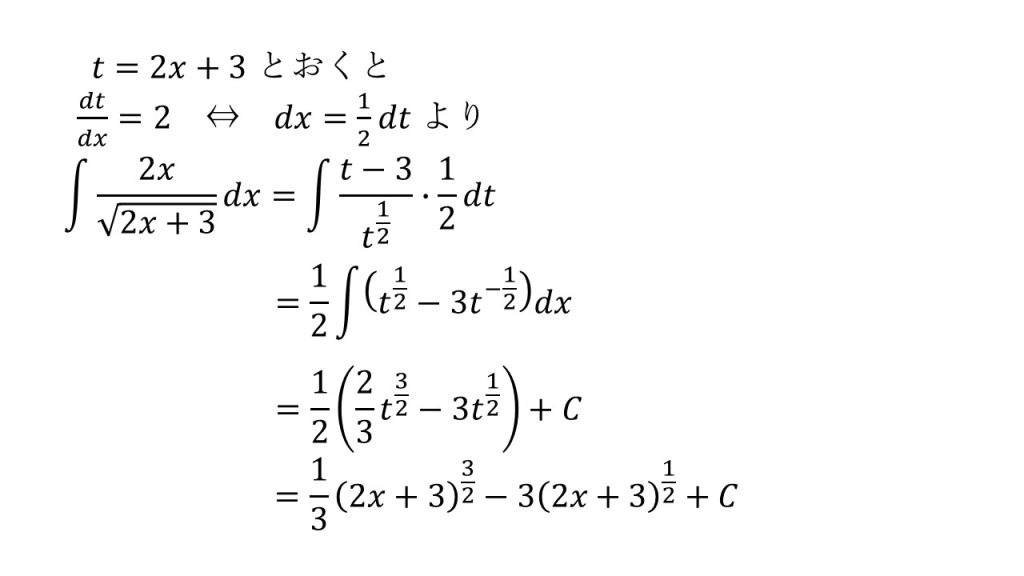
- 2x=t-3
- 置換積分法についてはこちら→置換積分法
④
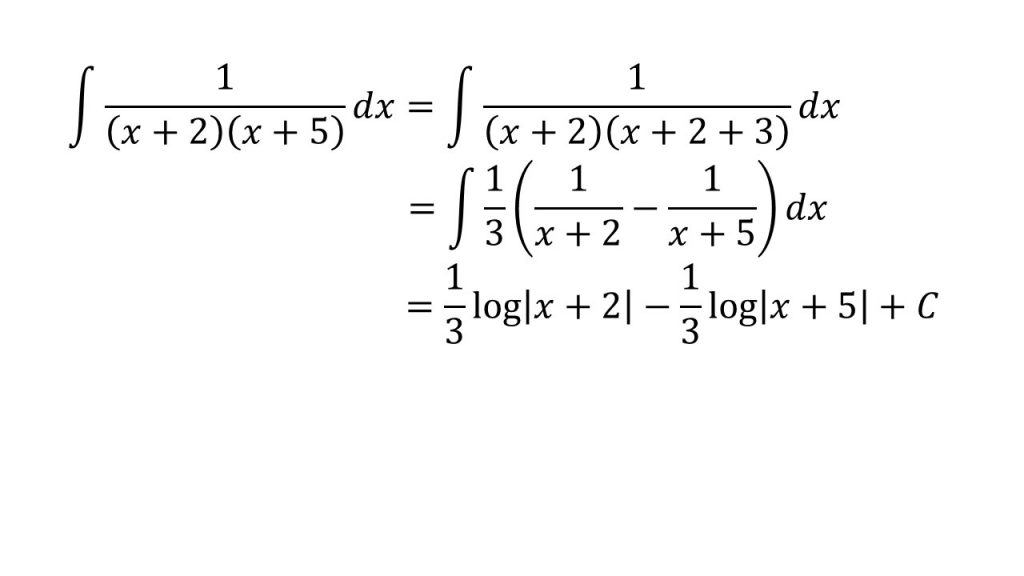
- 部分分数分解
- 部分分数分解のやり方に関してはこちら→部分分数分解のやり方
⑤
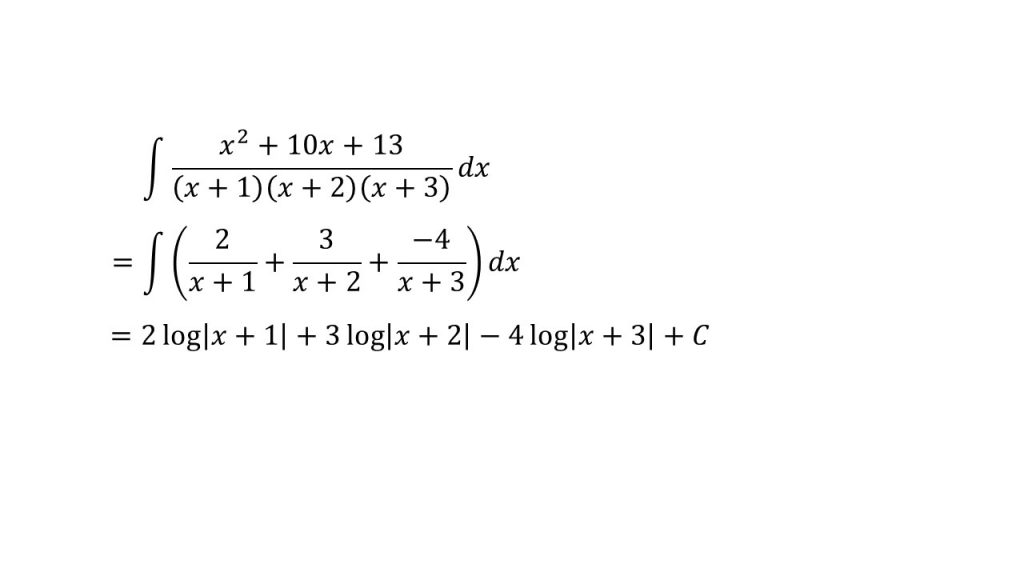
- 部分分数分解
- 部分分数分解のやり方に関してはこちら→部分分数分解のやり方
⑥
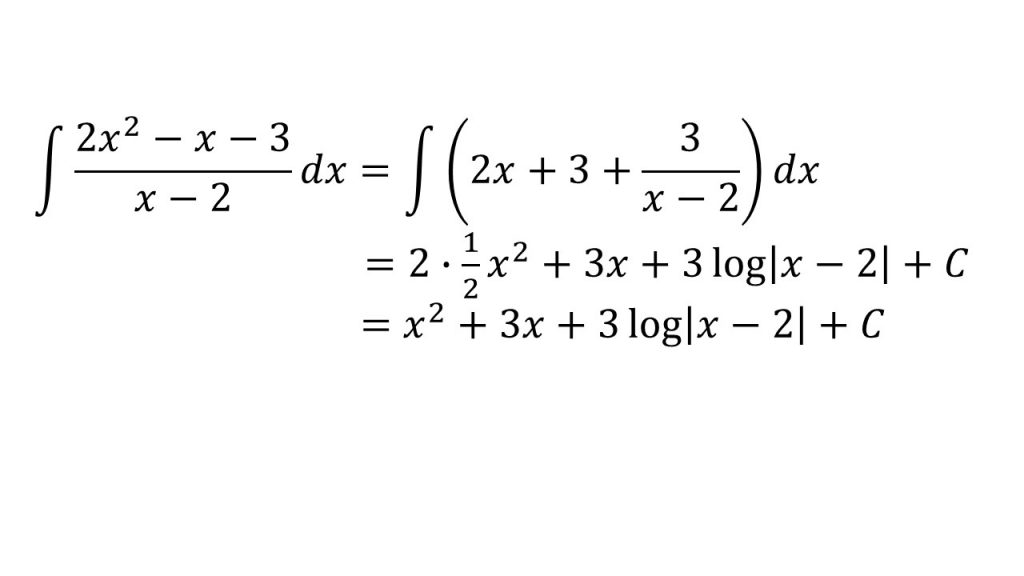
- 分母の次数≦分子の次数のとき→次数下げ
- 次数下げのやり方についてはこちらを参照してください→根号や虚数単位iを含む式を代入して式の値を求める問題の解法(次数下げ)
⑦
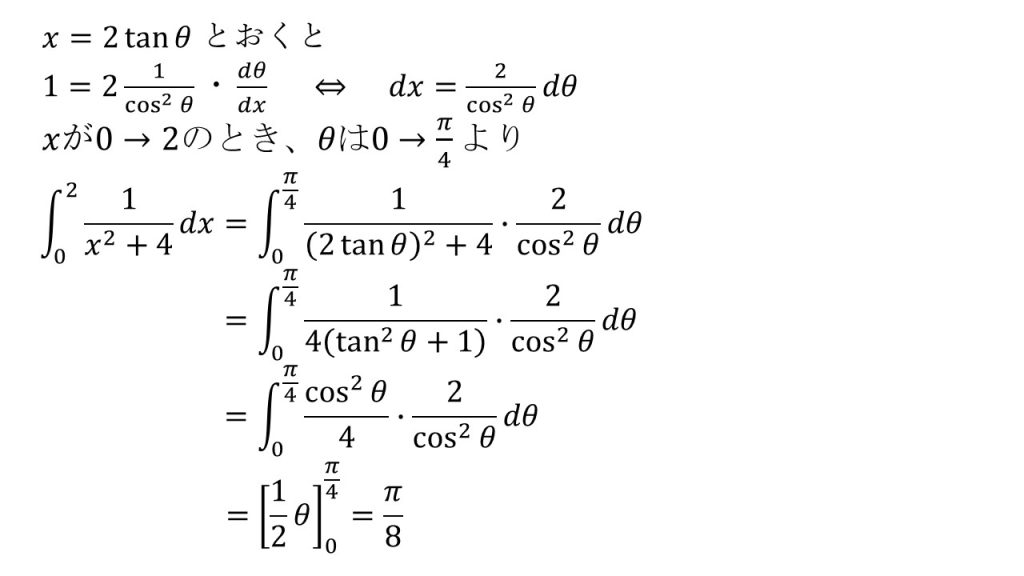
- 分母がx2+〇→x=2tanθと置換。これは特殊な置換なので覚えておこう!
⑧
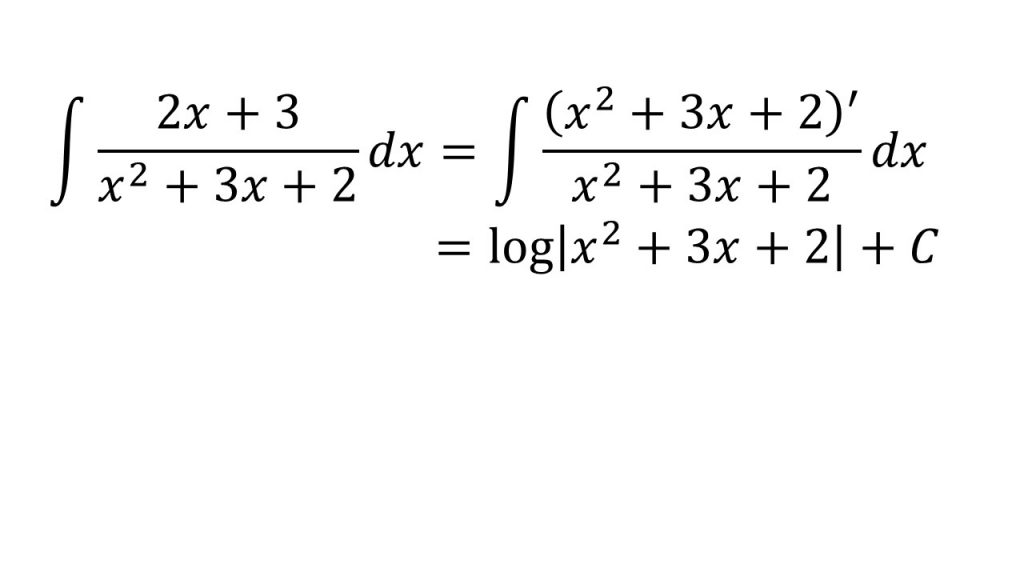
- f'(x)/f(x)の形にするパターン。なぜこれが成り立つか分からなければ、logf(x)を微分してみるとよい(対数関数の微分+合成関数の微分)。
⑨

- f'(x)/f(x)の形にするパターン。なぜこれが成り立つか分からなければ、logf(x)を微分してみるとよい(対数関数の微分+合成関数の微分)。
⑩
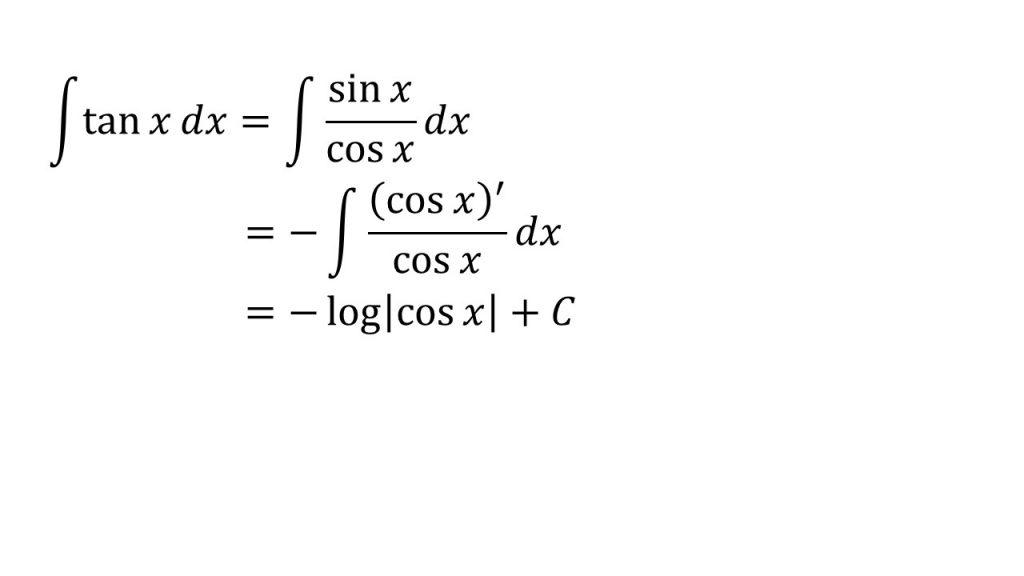
- f'(x)/f(x)の形にするパターン。なぜこれが成り立つか分からなければ、logf(x)を微分してみるとよい(対数関数の微分+合成関数の微分)。
⑪
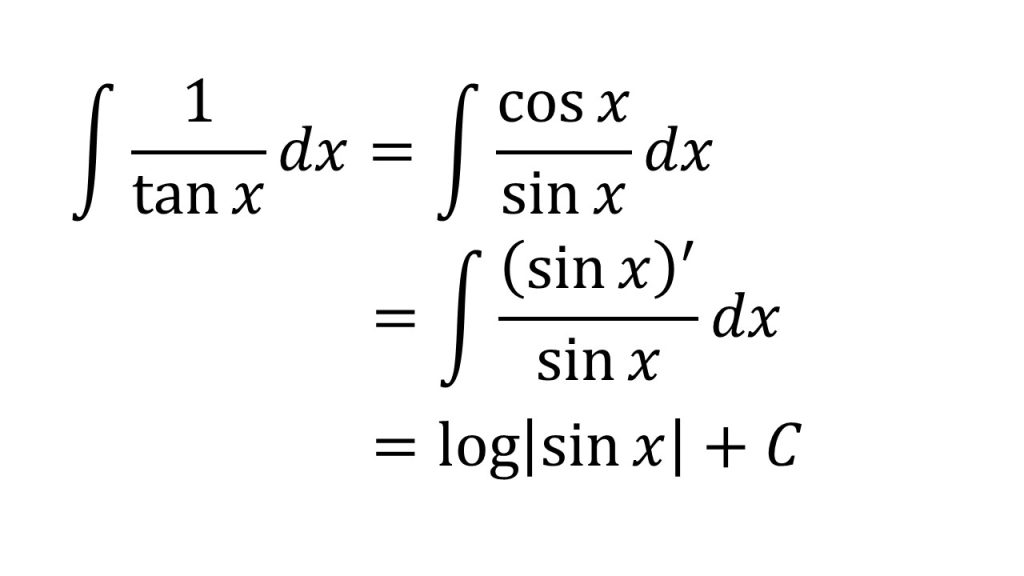
- f'(x)/f(x)の形にするパターン。なぜこれが成り立つか分からなければ、logf(x)を微分してみるとよい(対数関数の微分+合成関数の微分)。
⑫
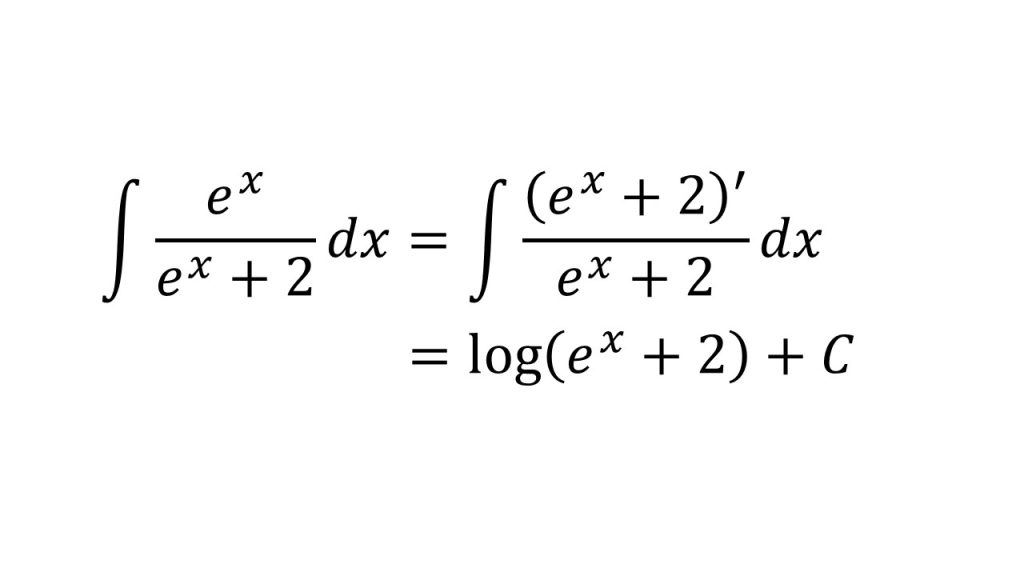
- f'(x)/f(x)の形にするパターン。なぜこれが成り立つか分からなければ、logf(x)を微分してみるとよい(対数関数の微分+合成関数の微分)。
☆問題のみはこちら→分数式の積分(問題)
【式の種類別演習問題一覧】
【パターン別演習問題一覧】
~参考~
☆積分計算(数学Ⅲ)をマスターしよう(解説・授業・公式・演習問題一覧)
☆積分(数学Ⅲ)の計算公式の証明はこちら→「積分は微分の逆である」ということを意識して積分の公式を理解しよう!
☆微分計算(数学Ⅲ)をマスターしよう(解説・授業・公式・演習問題一覧)
