(1)例題
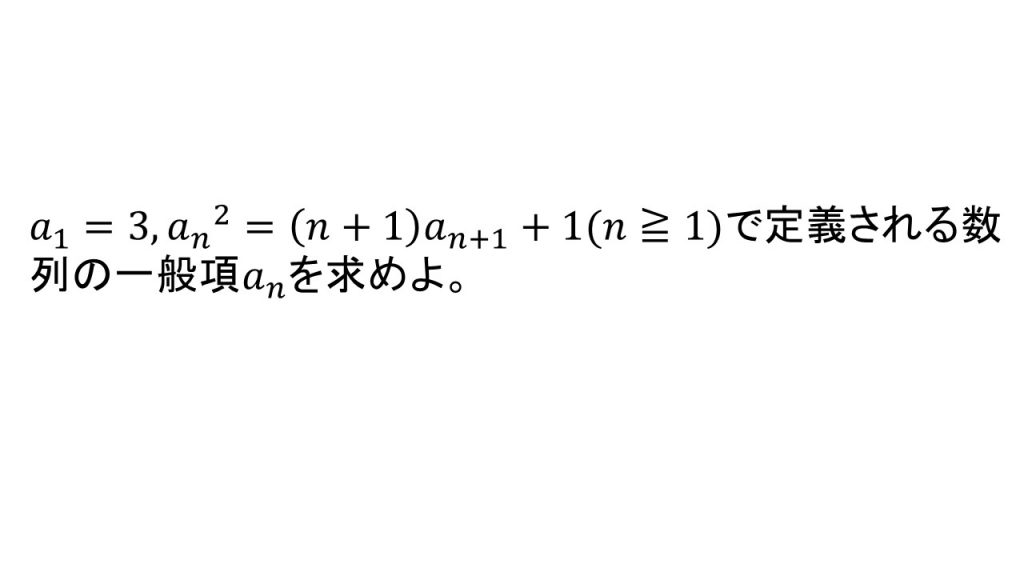
(2)例題の答案


(3)解法のポイント
通常の解法では解けない漸化式の一般項を求める場合は、n=1、n=2、n=3……と代入していき、一般項を予想します。
しかし、それではただの予想に過ぎず、答えにはならないので、その予想が正しいのかを証明しないといけません。
このように漸化式の一般項を予想して、その予想を証明する場合は、数学的帰納法を使います。
☆詳しい解説はこちら→漸化式をマスターしよう(3)応用パターン③(一般項を予想して数学的帰納法で証明するパターン、数学的帰納法の流れについても解説しています)
(4)必要な知識
①一般項を予想して数学的帰納法で証明するパターン

→一般項を予想して数学的帰納法で証明するパターンの漸化式解説動画
(5)理解すべきコア(解説動画)
①漸化式をマスターしよう(3)応用パターン③(一般項を予想して数学的帰納法で証明するパターン、数学的帰納法の流れについても解説しています)
(6)参考
☆漸化式をマスターしよう(3)応用パターン解説(隣接3項間漸化式、発想が難しい漸化式、一般項を予想して数学的帰納法で証明するパターン)
「漸化式をマスターしよう」シリーズは、『細野真宏の数列と行列が面白いほどわかる本 Version2.0』(細野真宏著、(株)中経出版発行、現在は絶版)を参考にしています。
細野真宏先生が現在発行している出版物はこちら(小学館HP)→https://www.shogakukan.co.jp/author/5885
中経出版の参考書・問題集はこちら(学参ドットコム)→https://www.gakusan.com/
