(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
RLC直列回路の式を、三角関数の合成を使って導いてみようと思います。
三角関数の合成を確認
まずは、三角関数の合成を簡単に確認します。

このように角度が同じsinとcosの足し算はsinだけの式にすることができます。このことを三角関数の合成といいます。
三角関数の合成の手順としては、まずsinの係数の分だけx軸方向に移動させ、次にcosの係数の分だけy軸方向に移動させた直角三角形をかきます。
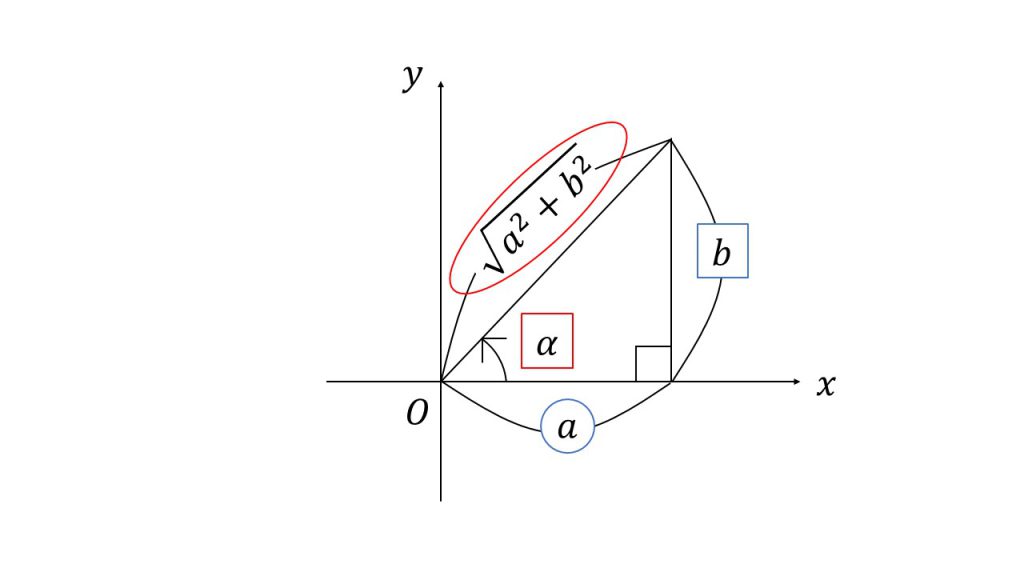
そして、その直角三角形の斜辺と角度を読み取り、斜辺の長さを係数に、直角三角形の角度を元の角度に足せば三角関数の合成ができます。
このαはこの直角三角形の角度なので、sinα=b/斜辺を満たし、cosα=a/斜辺を満たす角度となります。また、αをtanで説明する場合は、tanα=b/aとなります。
三角関数の合成についての詳しいことは数学IIの三角関数を復習するようにしてください。
RLC直列回路とは
それではRLC直列回路を考えてみます。
RLC直列回路は、下図のように交流電源に抵抗とコイルとコンデンサ−を直列でつないだ回路のことです。
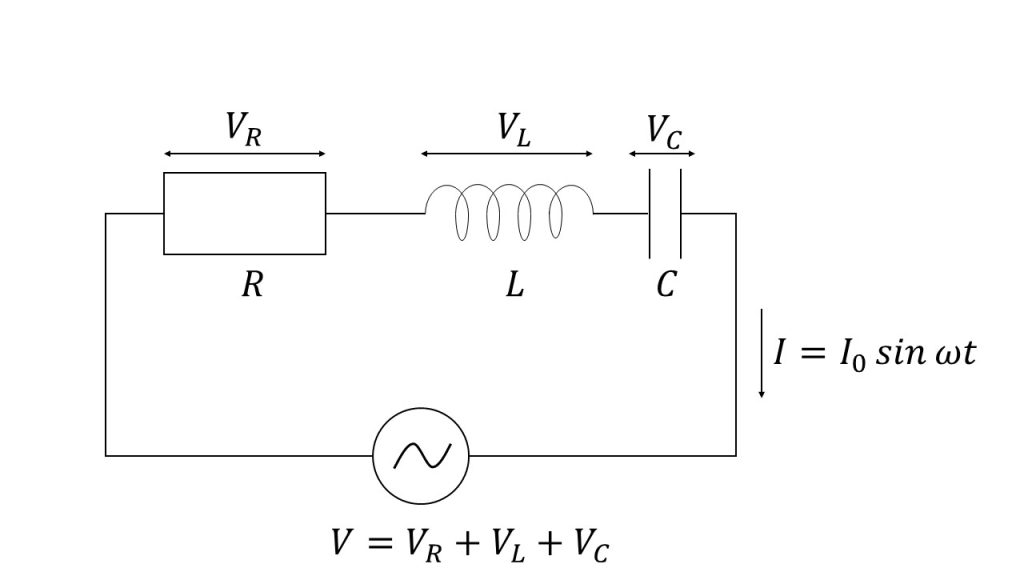
このRLC直列回路を考えるときのポイントは、抵抗、コイル、コンデンサーそれぞれで電圧は異なった値となりますが、直列回路なので、電流はどこでも同じ値となるということです。
また、それぞれの電圧を合計したものが電源の電圧となるので、
V=VR+VL+VC
となります。今回はこの電源の電圧の式を導いてみようと思います。
電源の電圧を求める
まずは、回路を流れる電流をI=I0sinωtとします。交流電源とは、電圧を時間とともに変化させる電源のことなのですが、その変化の仕方はsinの関数となります。そのため、電流もsinの関数となるので、電流の最大値をI0とし、このようにI=I0sinωtと設定してもいいのです。
それでは回路を流れる電流を設定したところで、まず、それぞれの電圧を求めてみます。まず抵抗における電圧は、抵抗における電圧の最大値をVR0としたとき、VR=VR0sinωtとなります。
そしてコイルにおける電圧は電流に対してπ/2進んでいるので、コイルにおける電圧の最大値をVL0とすると、VL=VL0sin(ωt+π/2)となります。
さらに、コンデンサーにおける電圧は、電流に対してπ/2遅れているので、コンデンサーにおける電圧の最大値をVC0としたとき、VC=VCosin(ωt−π/2)となります。
また、VR0をオ−ムの法則を使ってRI0と書き換えると
VR=VR0sinωt=RI0sinωt
となります。
そして、VL0は誘導リアクタンスを使ってωLI0と書き換えると
VL=VL0sin(ωt+π/2)=ωLI0sin(ωt+π/2)
となります。
さらに、VC0は容量リアクタンスを使って、I0/ωCと書くと
VC=VCosin(ωt−π/2)=I0/ωCsin(ωt−π/2)
となります。
電流に対して電圧がなぜ進んでいるのか、あるいは、なぜ遅れているのか、また、誘導リアクタンスや容量リアクタンスとは何かについては交流の基礎なので、もし分からない方がいれば交流の基礎を復習するようにしてください。
以上より、回路を流れている電流を設定することで抵抗、コイル、コンデンサーそれぞれの電圧を求めることができ、電源の電圧はこれらを足したものなので、Vは以下のように表すことができます。
V=RI0sinωt+ωLI0sin(ω+π/2)+I0/ωCsin(ωt−π/2)
あとはこの式を三角関数の合成を使って
◇sin(ωt+α)
このような形の式に変形します。
電源の電圧の式を三角関数の合成を使って式変形する
それでは、この電源の電圧の式を三角関数の合成を使って式変形します。
角度をそろえる
三角関数の合成をするためにまずしなければいけないことは、角度をそろえることです。三角関数が合成できるのは角度が同じになったときだからです。
そのため、sin(ωt+π/2)をcosωtとします。また、sin(ωt−π/2)を−cosωtとします。こうすることで、この3つの角度がそろいます。ちなみに、sin(ωt−π/2)が−cosωtになるのは、まず、sin(ω−π/2)を−sin(π/2−ωt)にして、sin(π/2−ωt)はcosωtなので、sin(ωt−π/2)=−cosωtとなります。
V=RI0sinωt+ωLI0sin(ω+π/2)+I0/ωCsin(ωt−π/2)=RI0sinωt+ωLI0cosωt−I0/ωCcosωt
この式変形には以下の3つの公式を使いました。
sin(θ+π/2)=cosθ
sin(−θ)=−sinθ
sin(π/2−θ)=cosθ
これらの公式が怪しい場合は数学IIの三角関数の性質を復習するようにしてください。
三角関数の合成をする
そして次に、I0cosωtでくくります。
RI0sinωt+ωLI0cosωt−I0/ωCcosωt=RI0sinωt+(ωL−1/ωC)I0cosωt
すると、角度が同じでsinとcosの足し算になっているので、三角関数の合成ができます。
まずはsinの係数分の底辺の長さで、cosの係数分の高さとなっている直角三角形を考え、その斜辺の長さが係数となり、この角度をαとすると、この式は次のように合成することができます。
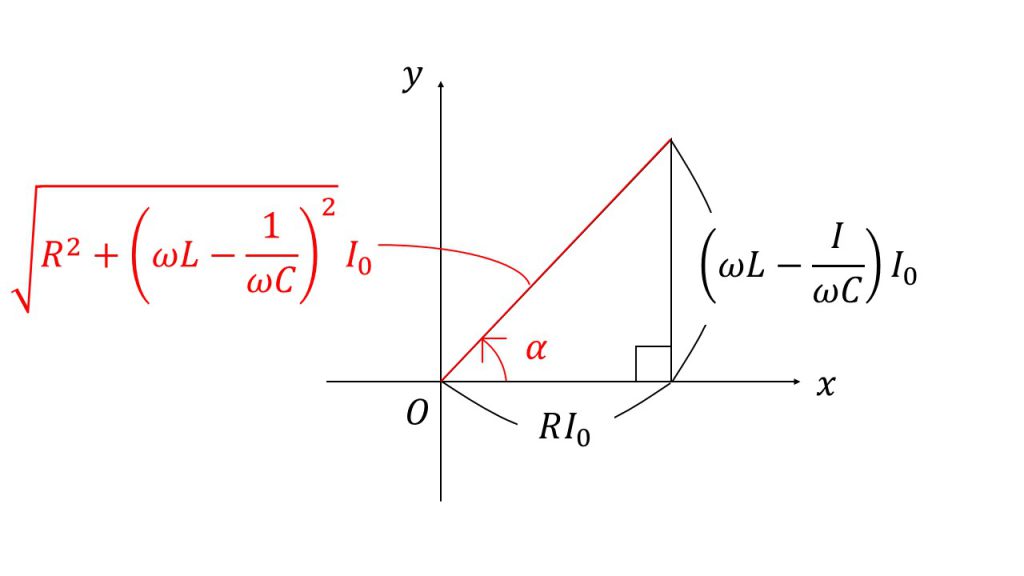
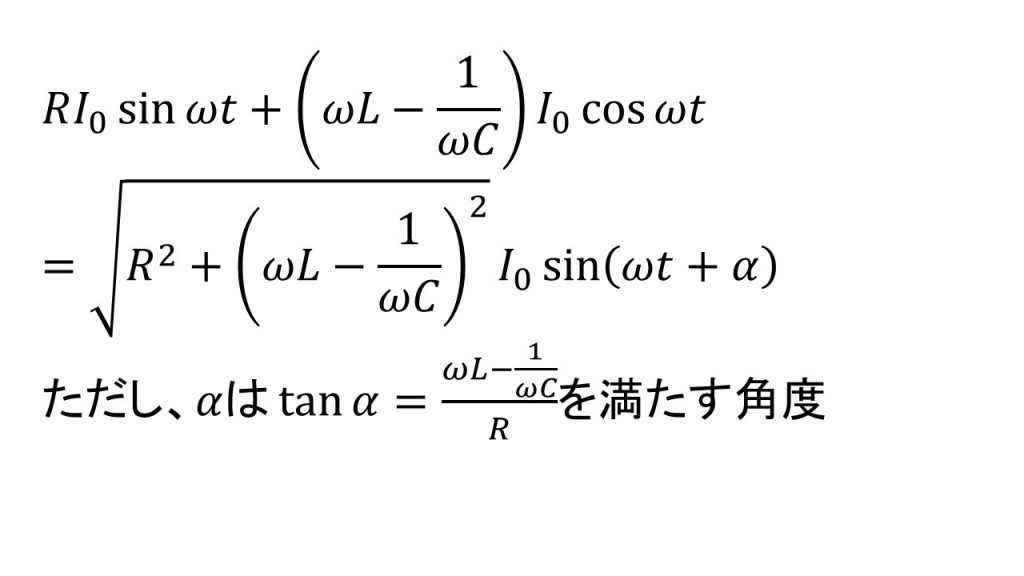
ちなみに、この
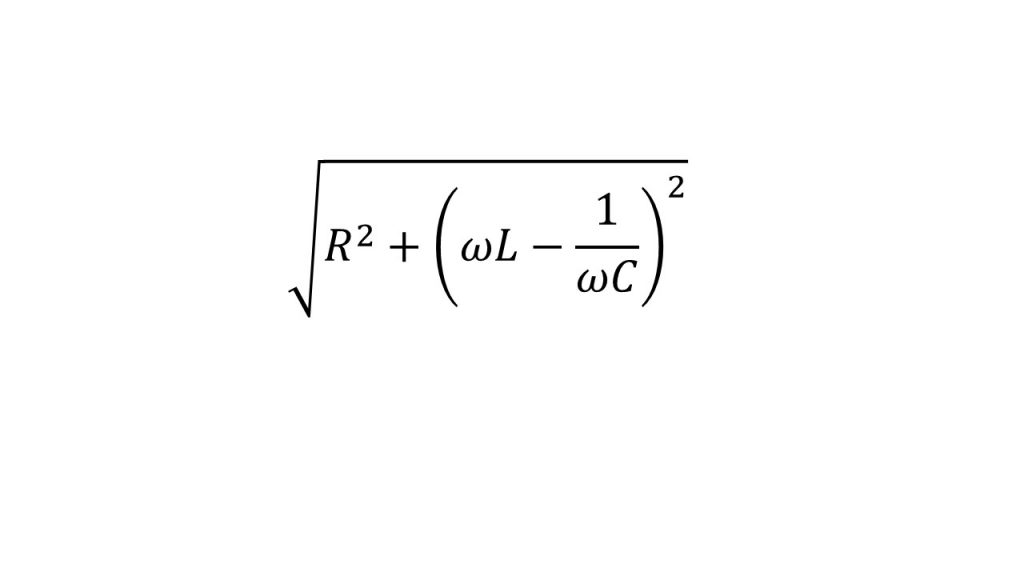
のことをインピ−ダンス、αのことを遅角といいます。
インピーダンスの補足
それでは最後に、インピ−ダンスと遅角について補足します。インピ−ダンスをZとすると、RLC直列回路の電源の電圧は
V=ZI0sin(ωt+α)
と書けます。
そして、sin(ωt+α)=1のときはV=ZI0となり、ZI0とはVの最大値を表しています。つまりV0=ZI0となり、この式はオ−ムの法則と同じ形になります。
よってインピ−ダンスとは、抵抗・コイル・コンデンサ−をまとめて1つの抵抗とみなしたものと考えることができます。
遅角についての補足
また、遅角についてですが、なぜ+なのに「遅れている角度」とよばれているかを説明します。
今回のように、電流を基準として電圧を表せば、「電圧の位相は電流の位相よりもαだけ進んでいる」と言えます。これはすなわち、電圧を基準とすると、「電流の位相は電圧よりもα遅れている」とも言えます。
それゆえに遅角とよばれているのです。
いかがだったでしょうか。RLC直列回路の電圧の式を導くときは、ベクトルを使うよりも三角関数の合成を使った方が式変形は簡単だったと思います。ぜひ自分でも三角関数の合成を使ってRLC直列回路の電源と電圧の式を導いてみてください。
(3)解説授業の内容を復習しよう
問題作成中
(4)交流と電気振動(電磁気)の解説一覧
②交流回路における抵抗・コイル・コンデンサーの考え方(なぜコイルとコンデンサーで電流と電圧の位相がズレるのか)
④RLC直列回路の式を三角関数の合成を使って導く(インピーダンスや遅角についても解説しています)
(5)参考
☆物理の解説動画・授業動画一覧(力学・熱力学・波動・電磁気・原子)
☆物理に関する現象や技術(力学、熱力学、波動、電磁気、原子)
