an+1=an+f(n)（階差数列を利用する漸化式）【漸化式をマスターしよう】

（１）例題

（２）例題の答案

（３）解法のポイント

a_n+1=a_n+f(n)の形の漸化式は階差数列を使った解法となります。a_nの係数が1であることに注意してください。a_nの係数が1でなければ階差数列を使った解法にはなりません。
※anの係数が1ではないときの解法→漸化式をマスターしよう（２）基本パターン⑧（最も重要なパターン、これが理解できたら漸化式の基本はマスターしたと言えます）

また、数列の問題でn-1を扱うときは、n≧2の場合分けと、後でn=1の確認をすることを忘れないようにしてください。

☆詳しい解説はこちら→漸化式をマスターしよう（２）基本パターン⑦（階差数列の公式を使うパターン）

（４）必要な知識

①階差数列の公式を使う漸化式

→階差数列の公式を使うパターンの漸化式解説動画

②Σの定義

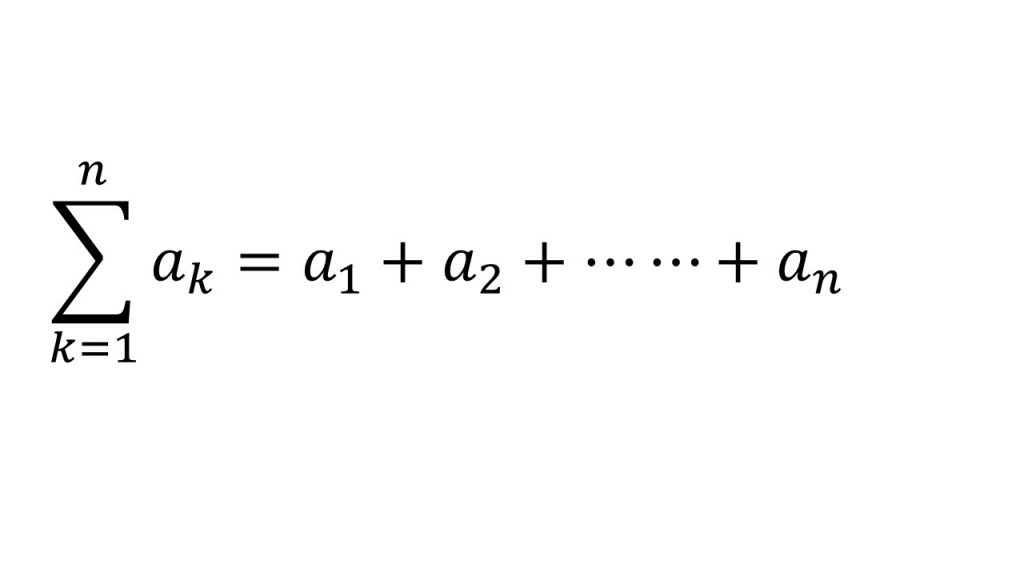
③Σの計算

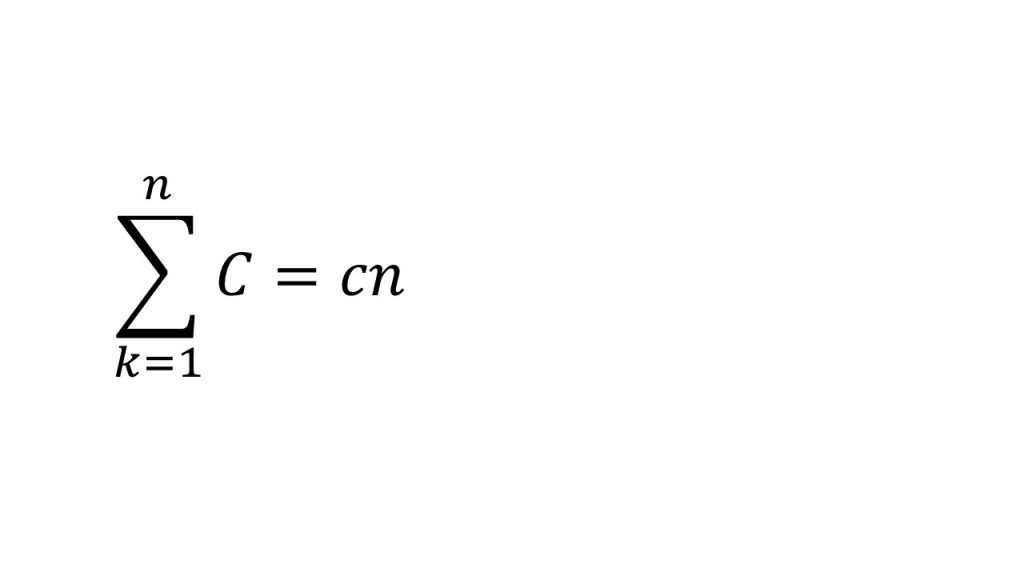
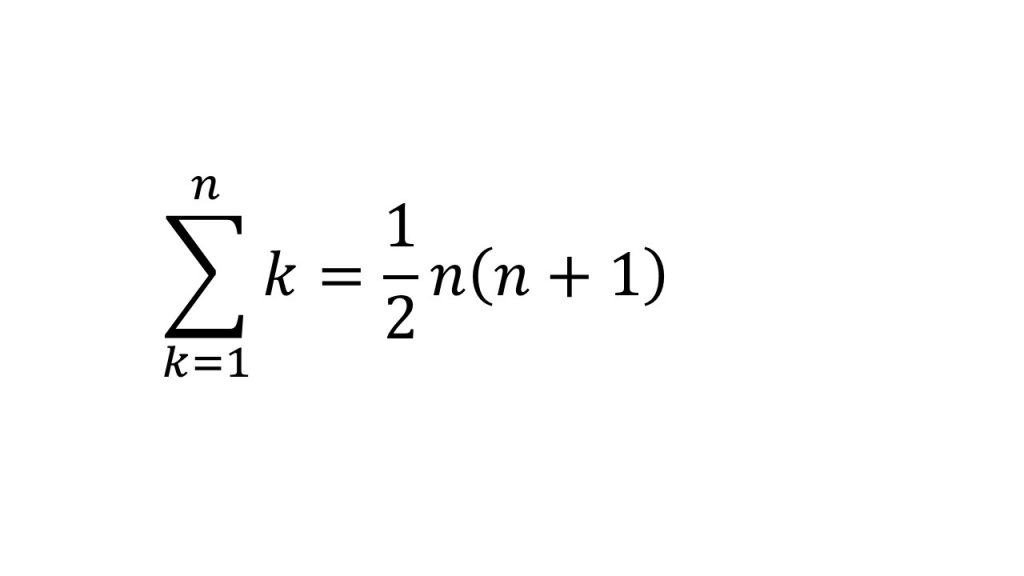
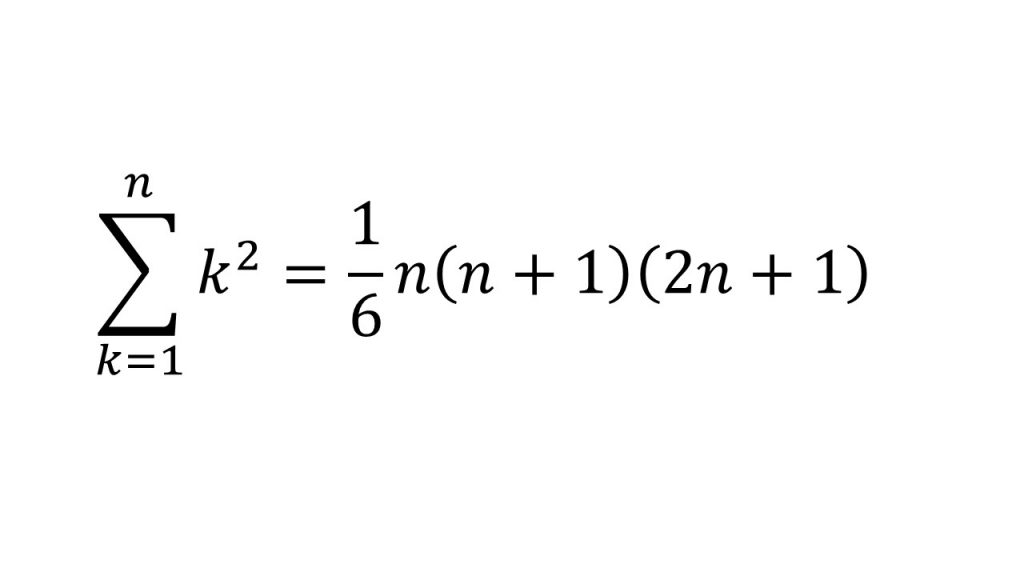
（５）理解すべきコア（解説動画）

①漸化式をマスターしよう（２）基本パターン⑦（階差数列の公式を使うパターン）

②階差数列の公式の原理（答案の書き方、なぜn≧2にするのか、そもそもなぜこの公式が成り立つのかについて解説しています）

（６）参考

☆漸化式をマスターしよう（２）基本8パターン

☆漸化式公式

☆漸化式（数学B）をマスターしよう

☆数学Bの勉強法

☆数学Bの解説動画・授業動画一覧

☆数学B公式一覧

☆数学の解説動画・授業動画一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学公式一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆計算のテクニック（数学）

☆絶対に知っておかないといけない数学の原則

☆数学に必要な思考法

☆数学学習に必要な参考書・問題集

---

「漸化式をマスターしよう」シリーズは、『細野真宏の数列と行列が面白いほどわかる本 Version2.0』（細野真宏著、(株)中経出版発行、現在は絶版）を参考にしています。

細野真宏先生が現在発行している出版物はこちら（小学館HP）→https://www.shogakukan.co.jp/author/5885

中経出版の参考書・問題集はこちら（学参ドットコム）→https://www.gakusan.com/