(1)例題

(2)例題の答案
①
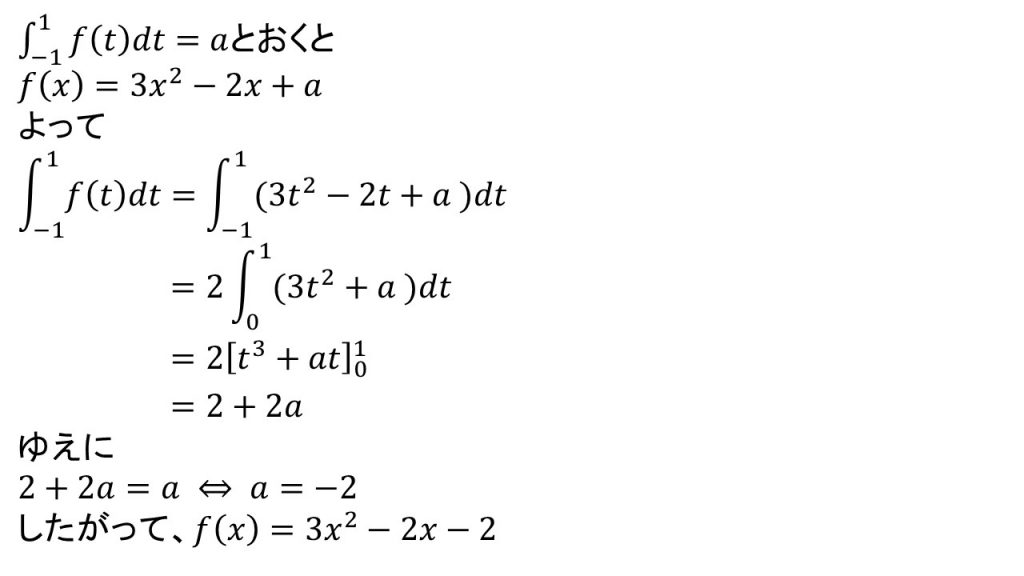
②
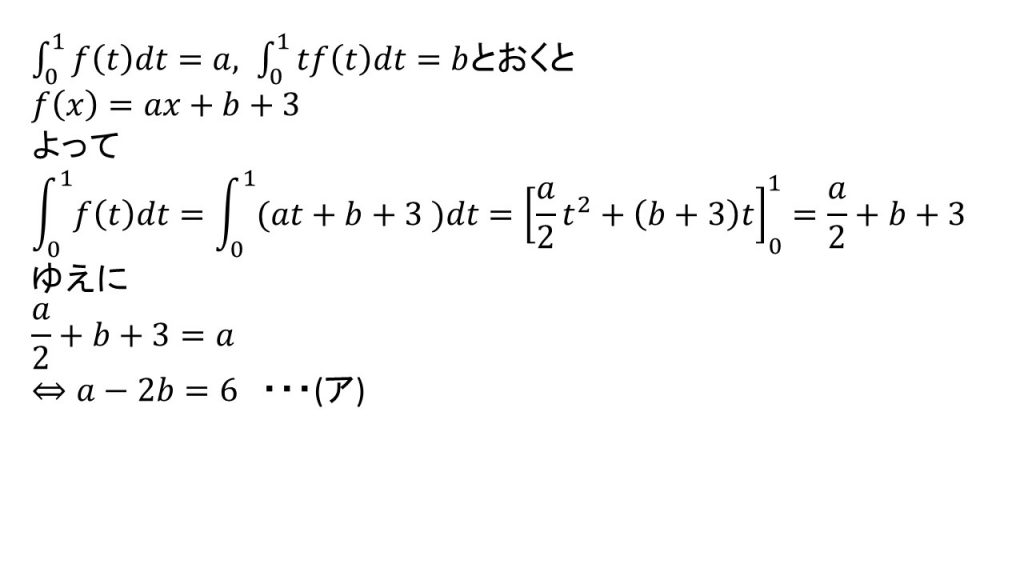
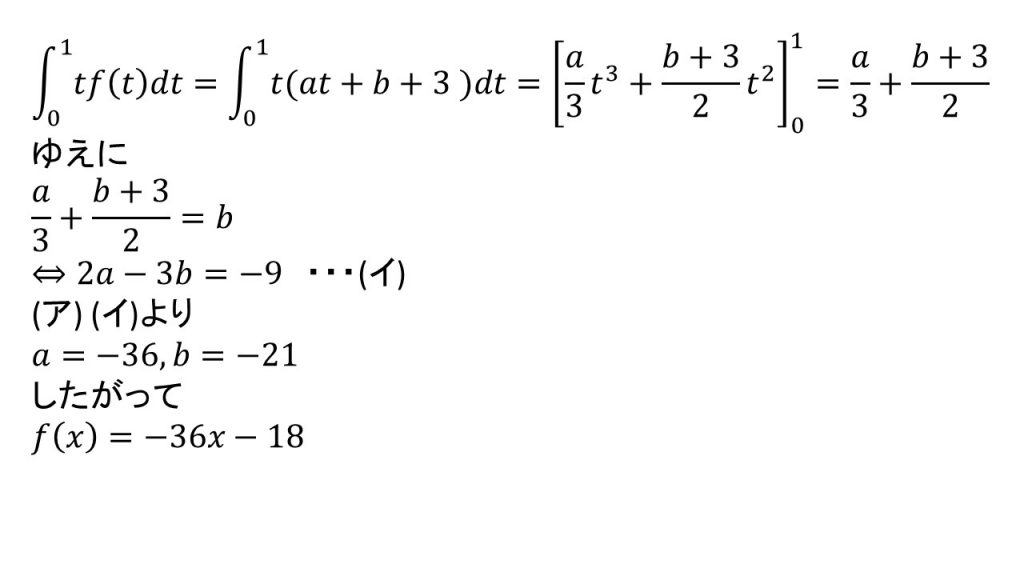
(3)解法のポイント
tはxとは無関係なので、tの式は定数として扱います。
つまり、tの定積分の部分は答えがどのようになろうとも定数なので、=aとまとめておいてしまってもOKです。
すると、例えば、(1)なら、
f(x)=6x²-x+a
となります。
つまり、
f(t)=6t²-t+a
なので、これを-1から1までの積分区間で定積分するとaを求めることができ、f(x)も求めることができます。
(1)例題

(2)例題の答案
①
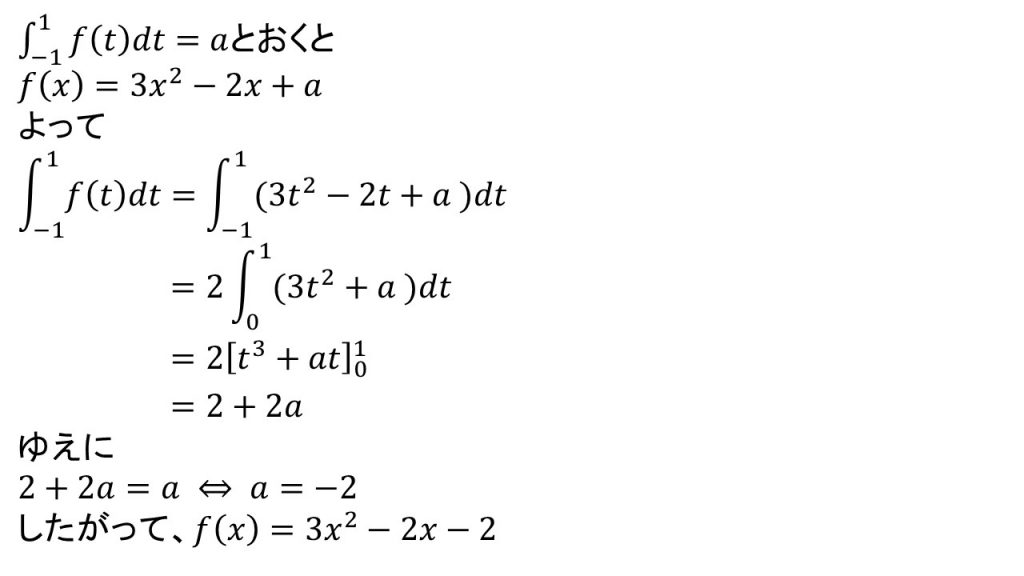
②
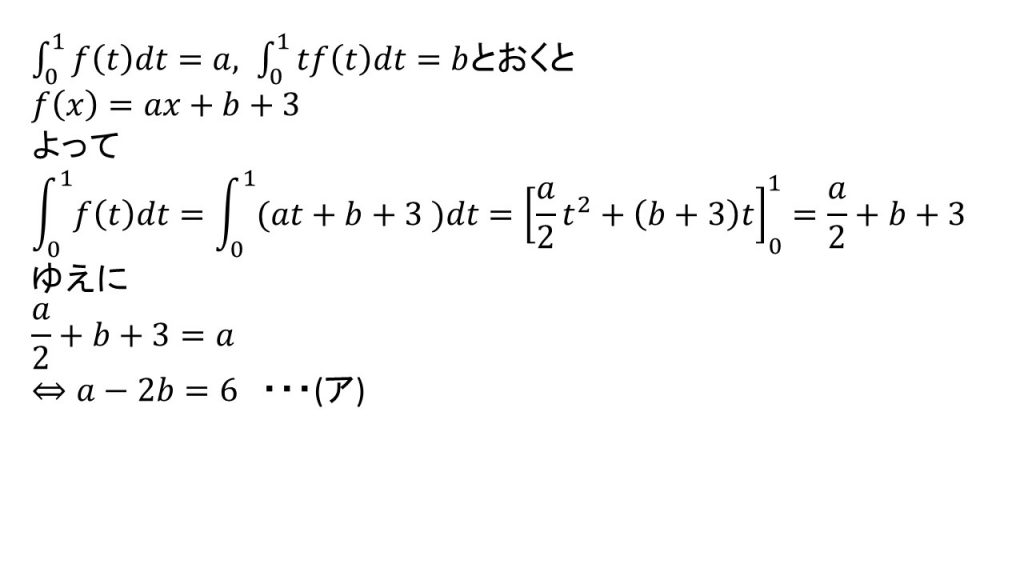
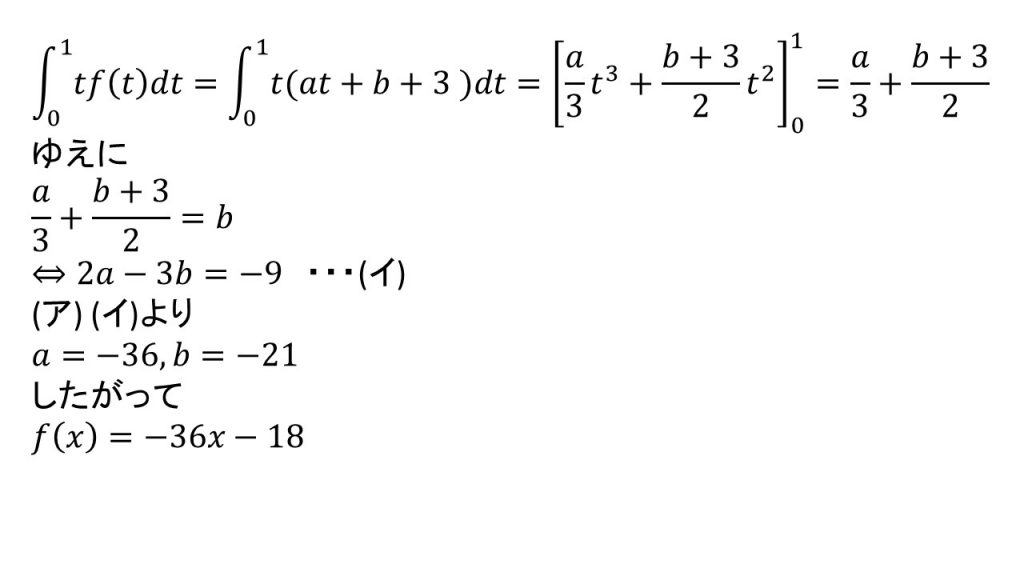
(3)解法のポイント
tはxとは無関係なので、tの式は定数として扱います。
つまり、tの定積分の部分は答えがどのようになろうとも定数なので、=aとまとめておいてしまってもOKです。
すると、例えば、(1)なら、
f(x)=6x²-x+a
となります。
つまり、
f(t)=6t²-t+a
なので、これを-1から1までの積分区間で定積分するとaを求めることができ、f(x)も求めることができます。