漸化式をマスターしよう（２）基本8パターン解説（①特性方程式を利用する漸化式、②n乗の項を含む漸化式、③分母と分子にanを含む漸化式、④anan+1を含む漸化式、⑤anにルートや指数がついている漸化式、⑥和Snが与えられているパターン、⑦階差数列の公式を使うパターン、⑧an+1=pan+f(n)）

（１）解説授業動画

• 前：漸化式をマスターしよう（１）基本中の基本（等差数列の漸化式、等比数列の漸化式、そもそも漸化式とは何か）
• 次：漸化式をマスターしよう（３）応用パターン解説（隣接3項間漸化式、発想が難しい漸化式、一般項を予想して数学的帰納法で証明するパターン）

☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル

（２）解説授業の原稿

①特性方程式を利用する漸化式（a_n+1=pa_n+q）

それでは基本のパターンを8つ解説します。

まずは基本パターン①：a_n＋1=pa_n+qを解説します。このパターンの漸化式は、この後に解説する漸化式の基本となっているパターンなので必ず解けるようにしてきましょう。

まず注意しておきたいのは、この漸化式は等差数列でも等比数列でもありません。a_nの係数が1であれば等差数列で、定数項がなければ等比数列なのですが、この漸化式には両方あるので、等差数列の解き方も等比数列の解き方も使えません。

• 漸化式をマスターしよう（１）基本中の基本（等差数列の漸化式、等比数列の漸化式、そもそも漸化式とは何か）

では、どのようにこのパターンの漸化式を解けばよいのかというと、特性方程式というものを使って解きます。特性方程式とは何かについては、実際に使っていくところを見てもらったほうが早いと思うので、早速この

a₁=1、a_n+1=2a_n+1

の漸化式を答案を確認していきます。

まずは、a_n+1とa_nをαとした方程式を解きます。するとα=2α＋1となりα=−1となるので、a_n+1=2a_n+1は、

a_n+1+1=2(a_n+1)

に式変形することができると分かります。

このパターンの漸化式はa_n+1とa_nをαとおき、そのαを使って

a_n+1−α=p(a_n−α)

と一般的に式変形することができます。今回で言えば、α=−1なので、左辺はa_n+1−(−1)でa_n+1+1となり、右辺は2(a_n+1)となります。

実際にこのa_n+1+1=2(a_n+1)を展開して整理してみると、元の式a_n+1=2a_n+1に戻ります。つまり、漸化式a_n+1=2a_n+1と漸化式a_n+1+1=2(a_n+1)は同じものなので、漸化式a_n+1=2a_n+1を解くためには漸化式a_n+1+1=2(a_n+1)を解けばよいということになります。

そして、このa_n+1とa_nをαとおいた方程式のことを特性方程式と言うのです。つまり特性方程式とは、a_n＋1=pa_n+qからa_n+1−α=p(a_n−α)への式変形をするためのαを見つけることができる方程式ということになります。

では、なぜこのような式変形をする必要があるのでしょうか。それは、この先の答案を見れば分かります。

特性方程式を使って、a_n+1+1=2(a_n+1)に式変形をしたら、カッコの中のa_n+1をb_nとおきます。すると、a_n+1+1=2(a_n+1)の右辺は2b_nとなり、左辺はb_n＋1となります。なぜb_n+1となるかというと、このb_n=a_n+1の式のnの部分をn+1にしてみると、b_n+1=a_n+1+1となるからです。

そして、置きかえた後の式b_n+1=2b_nを見てみると、この漸化式は等比数列を表す漸化式となっています。つまり、この漸化式b_n+1=2b_nが表す数列{b_n}は、初項a₁+1で、公比が2の等比数列となります。数列{b_n}の初項つまりb₁がa₁+1となるのは、b_n=a_n+1の式のnに1を代入してみると、b₁=a₁+1となるからです。

よって、b_nは等比数列の一般項の式を使うと、b_n=(a₁+1)･2ⁿ⁻¹=2×2ⁿ⁻¹となるので、b_n＝2ⁿとなります。そして今回求めるものはa_nなので、b_n=a_n+1を代入して、a_n+1=2ⁿとなるので、a_n=2ⁿ−1となります。これで、この漸化式の一般項を求めることができました。

• 漸化式をマスターしよう（１）基本中の基本（等差数列の漸化式、等比数列の漸化式、そもそも漸化式とは何か）

最初にもお伝えしたとおり、このパターンの漸化式は他のパターンの漸化式を解く上での基本となるので、この答案の流れは必ず自分でできるようになっておきましょう。

ちなみに、なぜ特性方程式α=2α＋1を使えば、この式変形ができるかについては今回は割愛しますが、いつか機会があればまた解説しようと思います。

漸化式を解くための基本にして奥義

それではこれからこのパターンの漸化式の解法を踏まえた上で様々なパターンの漸化式を解いていきますが、その前に、漸化式を解くために必要な考え方を確認します。

漸化式を解くためには、まず左辺をn+1、右辺をnの形にします。そして、この形にすれば置き換えをすることができ、置き換えをすることでより簡単な漸化式となり、解くことができるようになります。

この流れこそが漸化式を解くための基本であり、奥義なのです。

例えば、今回の答案でいえば、a_n+1+1=2(a_n+1)の部分が左辺をn+1、右辺をnの形に式変形する段階です。左辺のn+1に対応する部分が、右辺ではnになっています。そして、それ以外の部分は同じ形となっています。この形にすることができれば、置き換えをすることでより簡単な漸化式となり、元の漸化式の一般項を求めることができます。

このように、左辺をn+1、右辺をnに置き換えて簡単な漸化式に直すという流れを意識すると、漸化式は解くことができます。

②n乗を含む漸化式

それでは次は、a_n+1=p･a_n+qⁿのようにn乗を含む項がある漸化式を解いてみます。

このタイプの漸化式のポイントは、両辺をqⁿ⁺¹で割ることです。実際にやってみましょう。

例えば、

a₁=2、a_n+1=4a_n+6･2ⁿ

の漸化式があった場合、2ⁿがあるので両辺を2ⁿ⁺¹で割ります。すると、

a_n+1/2ⁿ⁺¹=4a_n/2ⁿ⁺¹+6･2ⁿ/2ⁿ⁺¹

のようになります。

そしてここから式変形するのですが、ポイントは左辺をn+1、右辺をnとすることです。

2ⁿ⁺¹で割っているので、左辺はn+1となっています。しかし、右辺はこのままではnとn+1が混ざっています。そこで、2ⁿ⁺¹を2･2ⁿとして2と4で約分をすると、右辺は2･a_n/2ⁿとなります。また、6･2ⁿ/2ⁿ⁺¹の項も約分すると、3となります。

このようにすることで、左辺はn+1、右辺はnの形にすることができたので、a_n/2ⁿ=b_nと置くと、左辺はb_n+1となり、右辺は2b_n+3となります。そして、

b_n＋1=2b_n+3

は先ほど解いた特性方程式を使って解くパターンの漸化式となったので、もうこの漸化式は解くことができます。

• 漸化式をマスターしよう（２）基本パターン①（特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義）

特性方程式を使って、α=2α+3とするとα=−3となり、式変形をすると

b_n+1+3=2(b_n+3)

となり、置き換えをしてc_n=b_n+3とすると

c_n+1=2c_n

となって、等比数列となります。そして、c₁はb₁+3なので、

c_n=(a₁/2¹+3)･2ⁿ⁻¹=2ⁿ⁺¹

となり、c_nにb_n+3を代入すると

b_n=2ⁿ⁺¹−3

となります。

よって、b_n=a_n/2ⁿなので、

a_n=(2ⁿ⁺¹−3)･2ⁿ

となり、分配法則を使って展開すると

a_n=2²ⁿ⁺¹−3･2ⁿ

となります。

このパターンの漸化式も、先ほど確認した漸化式を解くための基本にして奥義の流れで解いています。まずは左辺をn+1、右辺をnの形にして、置きかえて、解くことができる漸化式にしています。

• 漸化式をマスターしよう（２）基本パターン①（特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義）

ちなみに、a_n+1=4a_n＋6･2ⁿのようにn乗を含む項があるので、両辺を2^n＋1で割ったわけですが、この2ⁿのn乗がn+1乗になっていたり、n−1乗になっていたとしても両辺を2ⁿ⁺¹で割ります。なぜなら、左辺をn+1にすることが目的だからです。

また、慣れてきたら置きかえはせずにそのまま解いても構いません。

③a_nが分母と分子に含まれている漸化式

それでは次は、a_n+1=a_n/pa_n+qのパターンの漸化式を解きます。

このように分母と分子にa_nを含むパターンの漸化式は両辺の逆数をとります。実際に

a₁=1、a_n+1=3−a_n/a_n

を解いていきましょう。

このように分母と分子にa_nを含む場合は両辺の逆数をとります。すると

1/a_n+1=3−a_n/a_n

このようになります。そして次に式変形をするのですが、やはり意識することは、左辺をn+1、右辺をnの形にすることです。つまり、右辺の分数をa_n/3−a_n/a_nと分解して、約分をして

1/a_n+1=3･1/a_n−1

とします。

このように式変形すると、左辺のn+1に対応する部分が右辺でnの形になっているので、1/a_n=b_nと置き換えることができ、このように置き換えると

b_n+1=3b_n−1

のように解くことができる簡単な漸化式になります。

• 漸化式をマスターしよう（２）基本パターン①（特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義）

あとは先ほどと同様に、特性方程式を使って解いていきます。α=3α−1とするとα=1/2となり、

b_n+1−1/2=3(b_n−1/2)

となり、b_n−1/2=c_nとおくと、

c_n+1=3c_n

となるので、

c_n=(1/1−1/2)･3ⁿ⁻¹=3ⁿ⁻¹/2

となり、

b_n=3ⁿ⁻¹/2＋1/2

となるので、

1/a_n=3ⁿ⁻¹/2＋1/2

となります。したがって、この両辺の逆数をとると

a_n=2/(3ⁿ⁻¹＋1)

となります。

少し注意したいのが、3ⁿ⁻¹/2+1/2の式の逆数をとるときに、3ⁿ⁻¹/2と1/2の2つの項をそれぞれバラバラに逆数でとって、2/3ⁿ⁻¹+2としてしまってはいけないということです。両辺の逆数をとるときは、(3ⁿ⁻¹+1)/2のように1つの分数にまとめてから逆数にするようにしましょう。

このパターンの漸化式もやはり左辺をn+1、右辺をnの形にして置き換えて簡単な漸化式にするという流れで解いています。

• 漸化式をマスターしよう（２）基本パターン①（特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義）

④a_na_n+1を含む漸化式

次は、a_n･a_n+1=pa_n+qa_n+1のパターンの漸化式を解きます。

a_n･a_n+1を含むパターンの漸化式は、両辺をa_n･a_n+1で割ります。実際にやってみましょう。

a1=1、9a_n･a_n＋1=a_n−2a_n+1

の漸化式は、まず両辺をa_n･a_n+1で割ります。すると、

9=1/a_n+1−2･1/a_n

になります。そして次に、左辺がn+1、右辺がnになるように式変形します。すると

1/a_n+1＝2･1/a_n+9

となり、左辺がn＋1、右辺がnの形になったら、1/a_n＝b_nで置き換えをすることができ、そして

b_n+1=2b_n+9

のように、解くことができる簡単な漸化式となります。

• 漸化式をマスターしよう（２）基本パターン①（特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義）

あとは特性方程式を使い式変形をします。α=2α+9とすると、α=－9となり、

b_n+1+9=2(b_n+9)

のようになりますが、今回はb_n+9をc_nと置き換えずに解いてみます。置き換えなかったとしても、b_n+9をまとめて1つの数列と考えて、初項b_n+9で、公比が2の等比数列となるので、等比数列の一般項の式に代入すると

b_n+9=(b₁+9)･2ⁿ⁻¹

となり、計算すると

b_n=5･2ⁿ−9

となります。b_n=1/a_nを代入して、

1/a_n=5･2_n−9

となり、両辺の逆数をとると答えは

a_n=1/(5･2ⁿ−9)

となります。やはり逆数にするときは、まとめて逆数にするのに注意しましょう。

くどいようですが、左辺をn+1、右辺をnの形にして、置きかえて簡単な漸化式にするという流れで解きます。

• 漸化式をマスターしよう（２）基本パターン①（特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義）

⑤a_nに√や指数がついている漸化式

それでは次は、a_nに√や指数がついているパターンの漸化式を解きます。

このようなパターンの漸化式は、両辺を対数でとります。ちなみに、√は1/2乗と表すこともできます。

• 指数法則を使いこなそう（累乗根は分数乗に、割り算や分数は－1乗にする）

それではこの

a₁=√5、a_n+1=√a_n

の漸化式を解きます。√a_nのようにa_nに√がついている場合は、両辺を対数でとります。このとき底は何にしても問題ありません。底を2にしても5にしても10にしても、あるいはeにしても構いません。今回は10を底とする対数で両辺を取り、

log₁₀a_n＋1=log₁₀√a_n

とします。ここから式変形をしていきます。

まず、√は先ほども確認した通り1/2乗のことなので、右辺はlog₁₀a_n^1/2となります。そして、対数の計算公式より、真数の累乗は対数の前に出すことができます。

• 対数（数学Ⅱ）公式一覧

そして、1/2log₁₀a_nにすると、左辺がn+1、右辺がnの形となったので、log₁₀a_n=b_nと置きかえると、この漸化式は

b_n+1=1/2b_n

と簡単な漸化式になります。そして、この漸化式は等比数列を表しており、初項がb₁つまりlog₁₀a₁で、公比が1/2の等比数列なので、

b_n=(log₁₀√5)･(1/2)ⁿ⁻¹

のようになります。

ここからはa_nを求めるために式変形していきます。(1/2)ⁿ⁻¹を対数の前に書き、√5はやはり5^1/2とすると、(1/2)ⁿ⁻¹･log₁₀5^1/2となり、そして今度は、対数の係数を対数の中に入れます。つまり、対数の係数は真数の累乗となるので、真数の部分の指数は1/2･(1/2)ⁿ⁻¹となり、

b_n=log₁₀5^{1/2･(1/2)^n−1}=log₁₀5^{(1/2)^n}

となります。そして、b_n=log₁₀a_nなので、

log₁₀a_n= log₁₀5^{(1/2)^n}

となり、両辺の真数をみると

a_n=5^{(1/2)^n}

となります。このような対数の方程式を解くときのポイントは、両辺を底が同じ対数のなかに全て入れてしまうということです。

このパターンもやはり基本の流れとなっています。

• 漸化式をマスターしよう（２）基本パターン①（特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義）

⑥和S_nと漸化式

次は和が与えられているパターンの解説をします。

和Snが与えられているときに使う2つの式

S_nつまりa_nの和が与えられているときは、

a₁=S₁
a_n=S_n－S_n−1　(n≧2)

の2つの式を使います。

S_nとはa₁からa_nまでの和のことなので、S₁とはa₁までの和ということになり、それはつまりa₁のことです。

また、S_n−1とはa₁からa_n−1までの和ということなので、S_nからS_n−1を引くことでa_nだけが残るので、これらの式が成り立ちます。

ただし、2番目の式（a_n=S_n－S_n−1）を使うときは、nは2以上でないといけません。なぜなら数列において項数は自然数でないといけないからです。もしnが1になってしまえば、n−1は0となってしまい、0番目が存在するということになってしまいます。このように、数列の単元においてn−1を扱うときは、nは2以上にしないといけないということは覚えておきましょう。

• 階差数列の公式の原理（答案の書き方、なぜn≧2にするのか、そもそもなぜこの公式が成り立つのかについて解説しています）

例題で解法を確認

それではこの問題を解いていきます。

S_n=−7+2n−a_nのときa_nを求めよ。

まずは、1番目の式を使ってa₁を求めていきます。このS_n=−7+2n−a_nの式のnを1にしてみます。すると、

S_n=−7+2･1−a₁

のようになり、S₁はa₁のことなので、左辺をa₁にして、

a₁=−7+2･1−a₁

となります。そして整理すると、a₁=−5/2となります。

続いて、「n≧2のとき」と書いてから、2番目の式a_n=S_n−S_n−1を使います。

a_n=S_n−S_n−1なので、S_nは問題文で与えられている式を代入し、S_n−1はS_nの式のnをn−1にしたものを代入します。そうすると、

a_n=−7+2n−a_n−{−7+2(n−1)−a_n−1}

となります。そしてこの式の両辺を整理すると、

a_n=1/2a_n−1+1

となります。

これは特性方程式を使って解くことができるパターンの漸化式です。

• 漸化式をマスターしよう（２）基本パターン①（特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義）

左辺がnで右辺がn−1になっているのがやりにくい場合は、nの部分をn+1にして考えてみるとよいでしょう。今回は左辺をn、右辺をn−1のままで解きました。

特性方程式をα=1/2α＋1とするとα=2となり、

a_n−2=1/2(a_n−1−2)

となり、置き換えを使うと、

b_n=1/2b_n−1

となります。するとb_nは公比が1/2の等比数列なので、

a_n−2=(a₁−2)･(1/2)ⁿ⁻¹

となります。よってa_nで解くと、

a_n=−9(1/2)ⁿ+2・・・(ア)

となります。

ただしこの問題はここでは終わりません。これではまだ答案の途中です。なぜなら、これまではn≧2のときの話をしているので、ここで終わってしまうとnが1のときもこの式（a_n=−9(1/2)ⁿ+2）が成り立つとは言えないからです。

よって、ここからはn=1のときもこの式（a_n=−9(1/2)ⁿ+2）が成り立つことを確かめます。a_n=−9(1/2)ⁿ+2の右辺にn=1を代入し計算すると、

−9･(1/2)+2=−5/2

となり、計算結果と最初に求めたa₁の値が一致するので、この式（a_n=−9(1/2)ⁿ+2）はn=1のときも成り立つことが確認できました。よって、全ての自然数nにおいてS_n=−7+2n−a_nになるときのa_nはa_n=−9(1/2)ⁿ+2となります。

n≧2のときとn=1のときで答えが変わってくることもあるので、a_n=S_n−S_n−1のときのように、数列の問題でn−1を扱うときは必ずn≧2のときを求めた後、n=1でも成り立つかどうかを確認しましょう。

⑦a_n+1=a_n+f(n)（階差数列を利用する漸化式）

それでは次はa_n+1=a_n+f(n)のパターンの漸化式を解きます。

f(n)は階差数列

このパターンの漸化式のポイントは、a_nの係数が1になっていることです。a_nの係数が1になっていればf(n)は階差数列となります。

なぜならこのパターンの漸化式は

a_n+1−a_n=f(n)

の形に式変形することができ、この式は、ある項からその前の項を引けばnを含んだ式f(n)、つまりなんらかの数列となっているということを意味しているからです。

よって、このf(n)が階差数列であると分かれば、

この階差数列を使った公式を使うことができます。階差数列を使った公式がなぜこのようになるかは、別の動画で解説しているので、ぜひそちらもご覧になってください。

• 階差数列の公式の原理（答案の書き方、なぜn≧2にするのか、そもそもなぜこの公式が成り立つのかについて解説しています）

特に注意したいのが、Σの上がn−1になっていることです。この公式はn−1を扱っているので、和が与えられているパターンと同様に、n≧2のときしかこの公式は使えません。

例題で解法を確認

以上の点に注意して、a₁=1、a_n+1=a_n+3n²−4nの漸化式を解いてみます。

まずはa_nの係数を見ます。今回はa_nの係数が1になっているので、3n²−4nはa_nの階差数列になります。したがって、答案は以下のようになります。

まずは必ずn≧2を記述して、階差数列の公式を使います。Σの上をn−1にするのを忘れないようにしましょう。また、Σの中の(3k²－4k)をnで書いてしまう人がよくいるのですが、必ずΣの下の文字と合わせてkで書くようにしましょう。

あとは、このΣの計算をしていきます。Σは分配法則が成り立つので、

Σ(3k²－4k)=3Σk²－4Σk

のように分配し、

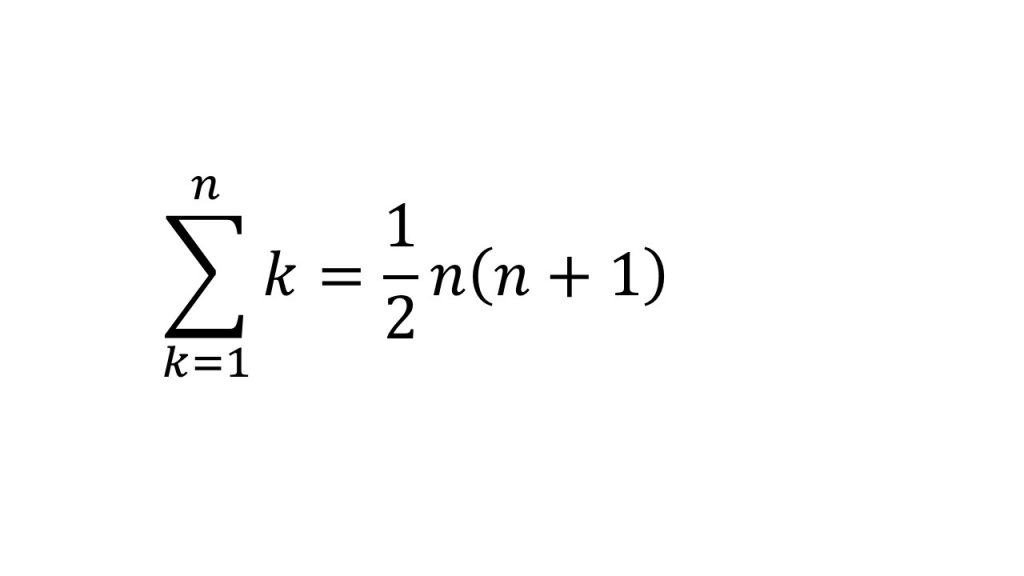
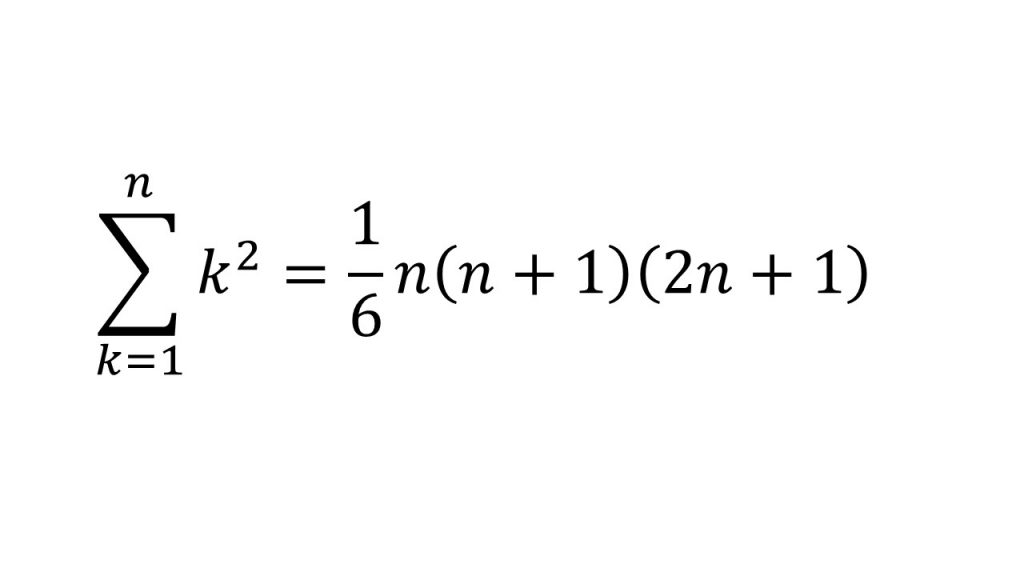
これらの公式を使っていきます。ただし、これらの公式を使うときに注意しなきゃいけないのは、Σの上がn−1になっているので、この2つの公式のnをn−1にしないといけません。それらに気をつけて計算すると、

a_n=1+3･1/6(n−1)･n･(2n−1)−4･1/2(n−1)･n

となります。

ここからの計算にもポイントがあり、全て展開して整理しようとするのではなく、まず分数でくくるようにしましょう。今回でいえば、約分をしたあとに3･1/6(n−1)･n･(2n−1)と、4･1/2(n−1)･nの項に1/2が残るので、全体を1/2でくくります。そうすると、1は2倍して2となり、真ん中の項+3･1/6(n−1)･n･(2n−1)は1/2が外に出て、最後の項−4･1/2(n−1)･nも2倍して係数が4となり、まとめると、

1/2{2+(n−1)･n(2n−1)−4(n−1)･n}

になります。このように分数で全体をくくると分数の計算をしなくてよくなるので、計算ミスが減り、正確にかつ速く計算することができるようになります。

最後にカッコの中を整理すると、a_n=1/2(2n³−7n²+5n+2)のようになります。

そして、ここで答えとしてはいけません。なぜなら、最初からここまではあくまでもn≧2のときの話をしているので、n=1のときもa_n=1/2(2n³−7n²+5n+2)が成り立つかは示されていないからです。

よって、n=1のときもこれが成ち立つことを確認するために、a_n=1/2(2n³−7n²+5n+2)の右辺にn=1を代入して計算してみます。そうすると、

1/2(2･1−7･1+5･1+2)=1

となるので、問題文で与えられているa₁=1と、1/2(2n³−7n²+5n+2)のnに1を入れたものが一致するので、a_n=1/2(2n³−7n²+5n+2)はa₁=1のときも成り立つことが分かります。よって、すべての自然数nにおいて、a_n=1/2(2n³−7n²+5n+2)となります。

• 階差数列の公式の原理（答案の書き方、なぜn≧2にするのか、そもそもなぜこの公式が成り立つのかについて解説しています）

⑧a_n+1=pa_n+f(n)（最も重要なパターンの漸化式）

それでは次は、a_n+1=pa_n+f(n)のパターンです。

これが基本のパターンの最後のパターンとなります。最後のパターンですが、このパターンは重要なパターンとなります。この漸化式の解法が理解できれば、漸化式の基本はマスターできたと言えます。

ではどのような漸化式か確認しましょう。

a_n+1=pa_n+f(n)の形の漸化式です。

先ほどの階差数列の公式を使った漸化式と形は似ていますが、今回はa_nの係数が1ではありません。もしa_nの係数が1であれば、このf(n)が階差数列となり、階差数列の公式を使って解くことができます。しかし今回はa_nの係数が1ではないので、f(n)は階差数列とはなりません。

• 漸化式をマスターしよう（２）基本パターン⑦（階差数列の公式を使うパターン）

ではこのパターンの漸化式はどのように解いたらいいのかというと、左辺がn+1、右辺がnの形をムリヤリ作ることで解きます。

例題1：a_n+1+α(n+1)+β=p(a_n+αn+β)の形にムリヤリ式変形する

実際にやってみましょう。

a₁=0、a_n+1＝2a_n+2n−2

先ほども確認したとおり、a_nの係数が2となっているので、この2n−2は階差数列ではありません。また、a_n+1とa_nをαとした特性方程式を使って解くこともできません。なぜなら、この2n−2が定数ではなくnを含む式になっている場合は、特性方程式を使うことができないからです。

• 漸化式をマスターしよう（２）基本パターン①（特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義）

ではどのようにしたら良いかというと、左辺がn+1、右辺がnとなるような式変形を目指します。

a_n+1+2(n+1)=2(a_n+2n)のように、対応する場所の左辺ではn+1、右辺ではnの形になっており、それ以外が同じ形になっていれば、置き換えを使うことができるので、漸化式を解くことができます。

しかし、a_n+1＝2a_n+2n−2の式を見ただけで、a_n+1+2(n+1)=2(a_n+2n)のように式変形するのは難しいです。そこで、とりあえず分からない部分をα、βと置いて式を作り、そのαとβを求めていくという方針で答案を進めます。

まずは、

a_n+1+α(n+1)+β=2(a_n+αn+β)

のように、左辺はn+1の係数をαとし定数項をβとし、右辺はa_nの係数である2でくくったあと、nの係数をαとし定数項をβとします。次に、a_n+1+α(n+1)+β=2(a_n+αn+β)の式を展開して整理します。すると、

a_n+1=2a_n+(β−α)

となり、この式と元の式

a_n+1＝2a_n+2n−2

と比較して元の式ではnの係数が2なのでα=2となり、元の式は定数項が−2なのでβ−α=−2となります。あとはこの2つを連立させると、α=2、β=0と求めることができます。

αとβを求めたら、a_n+1+α(n+1)+β=2(a_n+αn+β)に求めたαとβを代入します。すると

a_n+1+2(n+1)= 2(a_n+2n)

のようになります。

つまり、この元の漸化式a_n+1＝2a_n+2n−2は、a_n+1+2(n+1)= 2(a_n+2n)のように式変形できるということになります。

このαとβは、a_n+1+2(n+1)= 2(a_n+2n)とa_n+1＝2a_n+2n−2が同じになるときのαとβなので、そのαとβを代入したら、a_n+1+2(n+1)= 2(a_n+2n)になっているので、元の漸化式a_n+1＝2a_n+2n−2と、このa_n+1+2(n+1)= 2(a_n+2n)は同じ式であるということになります。実際にa_n+1+2(n+1)= 2(a_n+2n)を展開して整理してみると、元の式a_n+1＝2a_n+2n−2に戻ります。

これで元の漸化式を左辺がn+1、右辺がnの形にできたので、a_n+2nをb_nとおくと、b_n+1=2b_nとなり、解くことができる簡単な漸化式となります。b_nは初項がb₁で、公比が2の等比数列なので、b_n=(0+2･1)･2ⁿ⁻¹の式となり、計算すると2ⁿとなります。よって、b_nにa_n+2nを代入してa_nで解くと、a_n=2ⁿ−2nとなります。

いかがでしょうか。このαとβを使ってムリヤリ式変形をするという答案の流れが理解できたでしょうか。このパターンの答案も結局のところ左辺をn+1、右辺をnの形にして置き換えて簡単な漸化式にするという基本の流れで解いているのです。

• 漸化式をマスターしよう（２）基本パターン①（特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義）

例題2：a_n+1+α(n+1)²+β(n+1)+γ=p(a_n+αn²+βn+γ)の形にムリヤリ式変形する

それではもう1問このパターンの問題を解いてみます。

a₁=0、a_n+1=2a_n+n²−n+1

今回はf(n)の部分がnの二次式になっています。しかし解法の流れは先ほどと同じです。それでは答案を確認していきます。

今回はf(n)の部分がnの二次式なのでα、β、γの3つの文字を使って、左辺がn+1、右辺がnの形となるようにします。

今回はnの2乗の項と作らないといけないので、左辺にはα(n+1)²が必要です。そして残りのnの項と定数項を調整するために、左辺にはβ(n+1)とγが必要になります。右辺はまずa_nの係数でくくったあと、左辺のn+1に対応する部分をnに変えます。そしてγはそのままγと書きます。すると、

a_n+1+α(n+1)²+β(n+1)+γ=2(a_n+αn²+βn+γ)

となります。

これでα、β、γを使って変形したい形の式を作ることができたので、α、β、γを求めるために、この式a_n+1+α(n+1)²+β(n+1)+γ=2(a_n+αn²+βn+γ)を展開して整理するとこのように、

a_n+1=2a_n+αn²+(−2α+β)n+(α−β+γ)

となります。よって元の漸化式

a_n+1=2a_n+n²−n+1

と比較すると、n²の係数が1になっているので、α=1となり、nの係数が−1なので−2α+β=−1となり、定数項が1なので−α−β+γ=1となります。あとはこの3つを連立させると、α=1、β=1、γ=3と求めることができます。

そして、ここで求めたα、β、γをa_n+1+α(n+1)²+β(n+1)+γ=2(a_n+αn2+βn+γ)に代入すると、

a_n+1+(n+1)²+(n+1)+3＝2(a_n+n²+n+3)

のようになります。つまり元の漸化式a_n+1=2a_n+n²−n+1は、この形a_n+1+(n+1)²+(n+1)+3＝2(a_n+n²+n+3)に式変形することができるということになります。実際にこの式a_n+1+(n+1)²+(n+1)+3＝2(a_n+n²+n+3)を展開して整理してみると、元の漸化式a_n+1=2a_n+n²−n+1に戻ります。

これで左辺がn+1、右辺がnの形ができたので、この2(a_n+n²+n+3)の部分をb_nと置くと、b_n+1=2b_nとなり、b_nは初項がb₁、公比が2の等比数列なので計算すると、b_n=(0+1+1+3)･2ⁿ⁻¹=5･2ⁿ⁻¹となります。よって、b_nにa_n+n²+n+3を代入してa_nで解くと答えは、a_n=5･2ⁿ⁻¹−n²−n−3となります。

いかがでしょうか。このf(n)がnの二次式であっても同様の解法で解けるということが分かったと思います。ちなみに、f(n) の部分はn乗などでも同様の流れで解くことができます。とにかく漸化式は左辺がn+1、右辺がnの形を作れば解くことができるのです。

（３）解説授業の内容を復習しよう

①漸化式の基本パターンを全てマスターしよう（問題一覧）

（４）漸化式をマスターしよう（数学B）の解説一覧

①漸化式（数学B）公式一覧

②漸化式をマスターしよう（１）基本中の基本（等差数列の漸化式、等比数列の漸化式、そもそも漸化式とは何か）

③漸化式をマスターしよう（２）基本8パターン（①特性方程式を利用する漸化式、②n乗の項を含む漸化式、③分母と分子にanを含む漸化式、④anan+1を含む漸化式、⑤anにルートや指数がついている漸化式、⑥和Snが与えられているパターン、⑦階差数列の公式を使うパターン、⑧an+1=pan+f(n)）

④漸化式をマスターしよう（３）応用パターン解説（隣接3項間漸化式、発想が難しい漸化式、一般項を予想して数学的帰納法で証明するパターン）

（５）数列（数学B）の解説一覧

①数列（数学B）公式一覧

②複利計算の解説（そもそも複利とは何か、積み立て預金の計算について解説しています）

③階差数列の公式の原理（答案の書き方、なぜn≧2にするのか、そもそもなぜこの公式が成り立つのかについて解説しています）

④数列を理解できているか試すことができる良問の解説（2015年センター試験本試数学ⅡB第3問を記述問題に改題しています）

⑤数学的帰納法の分かりやすい答案の書き方（等式バージョン）

⑥数学的帰納法の分かりやすい答案の書き方（不等式バージョン）

（６）参考

☆漸化式をマスターしよう（数学B）解説動画・授業動画一覧

☆漸化式（数学B）公式一覧

☆漸化式（数学B）をマスターしよう（漸化式全パターンの解説・授業・演習問題一覧）

☆数列（数学B）公式一覧

☆数列（数学B）の解説・授業・公式・演習問題一覧

☆数学的帰納法（数学B）の解説・授業・公式・演習問題一覧

☆数学Bの解説動画・授業動画一覧

☆数学B公式一覧

☆数学Bの解説・授業・公式・演習問題一覧

☆数学Bの典型パターン一覧

☆数学の解説動画・授業動画一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学公式一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の解説・授業・公式・演習問題一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学典型パターン一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の語呂合わせ

☆数学学習に必要な参考書・問題集

---

「漸化式をマスターしよう」シリーズは、『細野真宏の数列と行列が面白いほどわかる本 Version2.0』（細野真宏著、(株)中経出版発行、現在は絶版）を参考にしています。

細野真宏先生が現在発行している出版物はこちら（小学館HP）→https://www.shogakukan.co.jp/author/5885

中経出版の参考書・問題集はこちら（学参ドットコム）→https://www.gakusan.com/