(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
気体の性質は、ミクロな視点つまり気体分子で考えるとその原理が理解しやすくなります。
気体の圧力を気体分子で考える
まずは、気体の圧力を気体分子で考えてみましょう。物理で気体の圧力は、以下のように表されると習います。
P=Nmv2/3V
化学を選択していて物理を選択していない方もこの式は知っておきましょう。Pは気体の圧力でVは体積、そしてNが気体分子の分子数、mが気体分子の質量で、vが気体分子の速さとなっています。
この式が意味することでまず重要なのが、気体の圧力は気体の分子数に比例するということです。
なぜそうなるのかは、この式の導き方を知っていれば理解できます。今回この式の導出は省略しますが、物理選択者であれば必ず自分でこの式を導けるようにしましょう。
物理を選択していない方も、この式は気体分子が壁に及ぼした力積から求めているということは知っておきましょう。
力積とは、気体分子が壁に衝突したときに生じるものです。つまり、気体の圧力は気体分子が壁にぶつかった結果生じているものであると考えることができるということです。
そのため、よりたくさんの気体分子が壁にぶつかった方が気体の圧力は大きくなり、逆に、壁にぶつかる分子が少なくなった方が気体の圧力は小さくなるということが言えます。
このように、気体の性質を考えるうえで、気体の圧力は気体分子が壁にぶつかって生じていると考えることはとても重要になります。
混合気体を気体分子で考える
それでは次に、混合気体を気体分子で考えてみます。以下のように、容積Vの容器に気体Aと気体Bを混ぜて入れます。

前提として、理想気体であれば、それぞれの気体分子はぶつかったり分子間力によって影響を受けたりすることなく、容器全体に拡散していきます。このような前提のもとであれば、気体Aも気体Bもそれぞれの運動に関わり合うことなく容器全体に広がっていきます。
混合気体の状態方程式
そのため、Aの分圧をPA、Aの物質量をnA、Bの分圧をPB、Aの物質量をnBとすると、
PAV= nART
PBV= nBRT
といった状態方程式が立てられ、さらに、AとBの全圧をPとすると、
PV= (nA+nB)RT
といった状態方程式が立てられます。
このとき注意したいのが、この3つの状態方程式のVは全て同じものであるということです。それぞれがお互い関係なく容器いっぱいに拡散するので、Aにとっての容積も、Bにとっての容積も、AとBを混ぜたものにとっての容積も全て同じVになるのです。
ドルトンの分圧の法則
したがって、これらの式から、全圧は各成分気体の分圧の合計となるという関係が成り立ちます。
P=PA+PB
この関係のことをドルトンの分圧の法則といいます。
また、PAV=nARTとPBV=nBRTの2つの式から、分圧の比はその成分気体の物質量の比になっているということも言えます。
PA:PB=nA:nB
そして、これらも先ほどの気体の圧力は気体分子の衝突によって生じているという考え方で考えてみると、AとBが壁にぶつかって生じた圧力は、Aが壁にぶつかって生じた圧力とBが壁にぶつかって生じた圧力の合計になると考えることができ、そして、物質量とは粒子の数を表しているので、AとBの分圧の比はAの気体分子の数とBの気体分子の数の比に等しくなると考えることができます。
気体分子の運動エネルギー
気体の圧力と運動エネルギー
また、先ほどの気体の圧力の式をこのように式変形してみます。
P=Nm/3V=2/3×N/V×1/2mv2
すると、1/2mv2つまり運動エネルギーの式を作り出すことができます。このことが意味していることは、気体の圧力は気体分子の運動エネルギーに比例するということです。
これも気体分子の衝突によって気体の圧力が生じているという考え方で理解することもできます。
つまり、運動エネルギーが大きいということはそれだけ運動が激しいということなので、壁にぶつかるときの勢いも大きくなります。気体分子がゆっくり壁にぶつかるときよりも、勢いよく衝突するときの方が気体の圧力が大きくなるというように考えることができます。
気体分子の運動エネルギーは絶対温度に比例する
また、気体分子の運動エネルギーは、ボルツマン定数kをつかって
1/2mv2=3/2kT
と表すことができます。物理選択者の方はこの式も導けるようにしておいてください。
このTは絶対温度のことなので、この式が意味していることは、気体分子の運動エネルギーは温度に比例しているということになります。
これもある意味当然で、温度を上げるということは気体分子の熱運動を激しくするということなので、それは気体分子の運動エネルギーが大きくなるということになります。
ちなみに、気体の内部エネルギーは気体分子の運動エネルギーをその分子数の分だけ合計したものなので、内部エネルギーも温度に比例することになります。
ボイルの法則を気体分子で考える
それでは次に、これまでの考え方を使ってボイルの法則とシャルルの法則を考えてみます。
まずはボイルの法則です。
PV=一定
となるのがボイルの法則です。なぜこの法則が成り立つかを考えてみましょう。
以下のように容積Vの容器の中に、ある気体が入っているとします。そしてこの容器の容積を半分にしてみます。それぞれで温度と気体の粒子数は変わらない場合、圧力がどうなるか考えてみましょう。
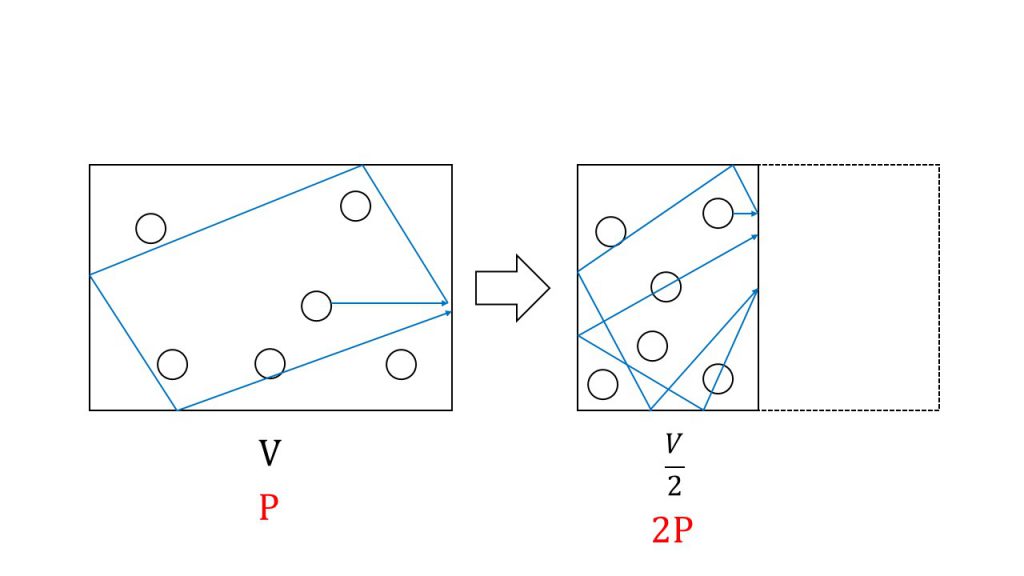
繰り返しになりますが、気体の圧力は気体分子が壁にぶつかった結果生じたと考えます。気体分子は自由に飛び回っているので、気体分子がある壁にぶつかったあとは、その分子は跳ね返って容器の中を飛び回り、またこの壁にぶつかっていきます。
ということは、容器の体積を小さくすると、気体分子が一定時間に壁にぶつかる衝突回数が増えるということになります。そのため、体積を半分にした場合は壁への衝突回数が2倍になるので圧力は2倍となります。よって、圧力と体積の積は温度を変えない限り常に一定となります。
シャルルの法則を気体分子で考える
それでは次にシャルルの法則を考えてみます。シャルルの法則とは、圧力を変えないとき、
V/T=一定
となるという法則です。こちらも気体分子の運動で考えてみます。
例えば以下のように体積を変えることのできる容器の中に気体を入れます。そして、外から気体を押す圧力を変えない状況で温度を2倍にしてみます。するとどうなるでしょうか。
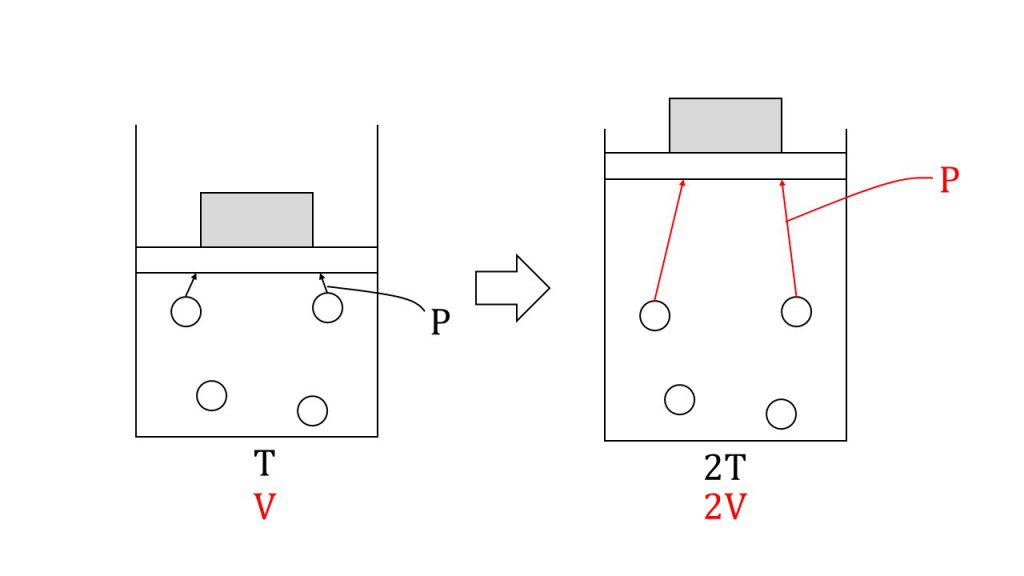
温度を上げるということは、気体分子の熱運動が激しくなるということであり、気体分子の運動エネルギーも2倍になるということになります。そのため気体分子はより激しく壁にぶつかっていきます。
しかし、外から気体を押す圧力は変わらないので、つり合うためには気体の圧力も変わらないようにしないといけません。
ではどうすればよいかというと、体積も2倍にすることで壁への衝突回数を半分にして圧力を一定に保つのです。よって、体積÷温度は常に一定の値となるのです。
気液平衡を気体分子で考える
最後に、気液平衡も気体分子で考えてみます。
気液平衡とは、液体表面の粒子が他の液体粒子からの分子間力を振り切って気体となっていく粒子の数と、気体分子が液体の粒子の分子間力につかまって液体になっていく粒子の数が等しくなったときを気液平衡といいます。
つまり簡単にいうと、蒸発する分子数と凝縮する分子数が等しくなったときを気液平衡といいます。

このようになると、蒸発と凝縮は起きてはいるのですが、気体部分の分子の数は常に一定となります。
ということは、気体の圧力も一定となります。そして、この一定になった圧力のことを飽和蒸気圧あるいは蒸気圧というのです。
飽和蒸気圧は温度にのみ依存しているということは重要なのであわせて知っておきましょう。
気液平衡の状態から体積を変えるとどうなるか
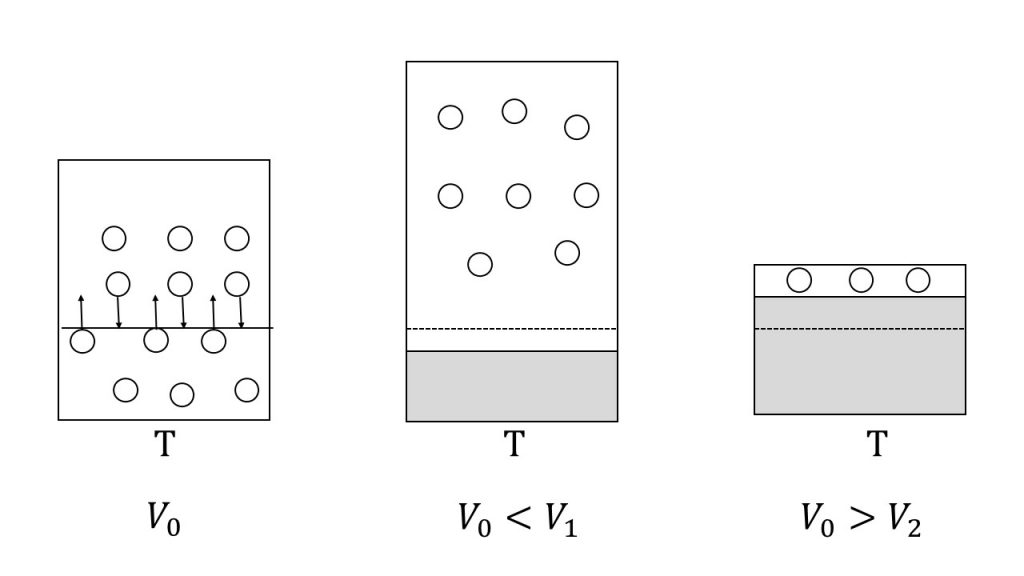
それでは気液平衡の状態から温度を変えずに体積だけ変えてみたらどのようになるか考えてみましょう。
先ほども確認した通り、温度を変えない限り飽和蒸気圧は変わりません。そのため、気体の圧力は変化しないようにしないといけません。
よって、体積を大きくした場合は気体分子の数がそのままだと壁への衝突回数が減ってしまうので、気体分子の数を増やさないといけません。したがって、液体の分子が気体分子になって気体分子の数を増やすので、液体の量は減少します。
また、体積を小さくした場合、圧力を変化させないようにするためには、気体分子の数を減らさないといけません。したがって、気体分子が液体になるので、液体の量は増加します。
このように、気液平衡も気体分子を考えることで理解しやすくなります。
いかがだったでしょうか。気体の性質も原理は気体分子で考えると理解しやすくなるということが分かったと思います。ぜひ今後気体の問題を考えるときは気体分子の運動を考えるようにしましょう。
(3)解説授業の内容を復習しよう
④気体の圧力・気体分子の運動エネルギー・気体分子の2乗平均速度・単原子分子の理想気体の内部エネルギーの4つを導けるようになろう。
(4)気体の性質(理論化学)解説一覧
①理想気体の状態方程式の使い方(理想気体とは何か、混合気体の考え方、計算の工夫の仕方についても解説しています)
②混合気体の計算の基本(全圧・分圧の考え方、ドルトンの分圧の法則についても解説しています)
③気体の燃焼(開放系)の計算(化学反応式を使った計算の仕方、燃焼の化学反応式の作り方についても解説しています)
④気体の燃焼(開放系)の計算の応用問題(複雑に見える問題でも1つの方程式にすることができます)
⑤気体の燃焼(閉鎖系)の計算(気液平衡とは何か、飽和蒸気圧の使い方、液体が存在するかどうかの判断の方法についても解説しています)
(5)気体の状態変化(熱力学)の解説一覧
②気体の性質は気体分子で考えることで理解しやすくなります(気体の圧力、混合気体、ドルトンの分圧の法則、気体の運動エネルギー、気体の内部エネルギー、ボイルの法則、シャルルの法則、気液平衡、飽和蒸気圧)
③理想気体の状態方程式の使い方(理想気体とは何か、混合気体の考え方、計算の工夫の仕方についても解説しています)
④気体の内部エネルギーの表し方(内部エネルギーの増加量の3つの表し方、熱力学の第1法則、定積変化、定圧変化、等温変化、断熱変化、マイヤーの関係についても解説しています)
⑤気体が吸収した熱量の求め方(定積モル比熱、定圧モル比熱、熱力学の第1法則、定積変化、定圧変化、等温変化、断熱変化、熱効率)
⑥気体が外部にする仕事(pΔVになるわけ、p-Vグラフ、熱機関のサイクル、定積変化、定圧変化、等温変化、断熱変化、断熱自由膨張)
⑦定積変化・定圧変化・等温変化・断熱変化におけるp-VグラフとV-Tグラフ(ポアソンの法則についても解説しています)
(6)参考(化学)
☆化学の解説動画・授業動画一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識テスト一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の解説・授業・知識・演習問題一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の語呂合わせ(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
(7)参考(物理)
☆物理の解説動画・授業動画一覧(力学・熱力学・波動・電磁気・原子)
☆物理に関する現象や技術(力学、熱力学、波動、電磁気、原子)
