(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
そもそも極値とは
そもそも極値とは関数の増加と減少が変わる場所のことを言います。
増加から減少に変わる場所のことを極大値といい、減少から増加に変わるところを極小値と呼んでいます。
導関数と極値
そして、増加と減少が変わる場所ということはつまり、その関数の導関数の正負が変わる場所でもあります。導関数が正であるということは元の関数は増加しているということであり、導関数が負であるということは元の関数は減少しているということを表しているからです。
さらに、導関数の正負が変わる場所があるということは、導関数のグラフがx軸より上の部分と下の部分の両方あるということにもなります。
例えば、関数f(x)が極大値をとるとき、導関数f’(x)がどのようになっているかというと、
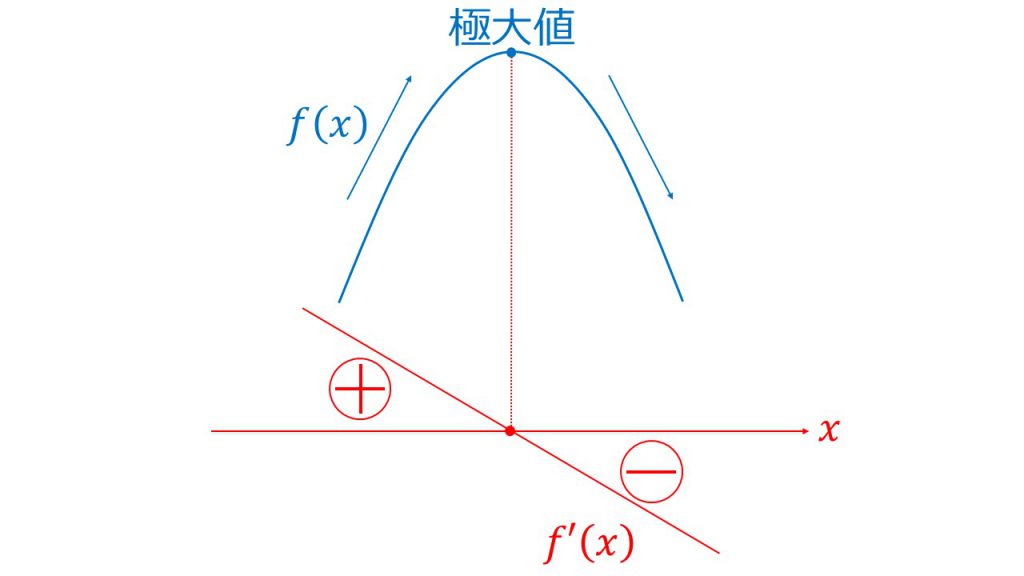
このようにx軸よりも上の部分つまりプラスとなっている部分と、x軸よりも下の部分つまりマイナスとなっている部分があるということになります。
またf(x)が極小値をもつときは導関数f’(x)は
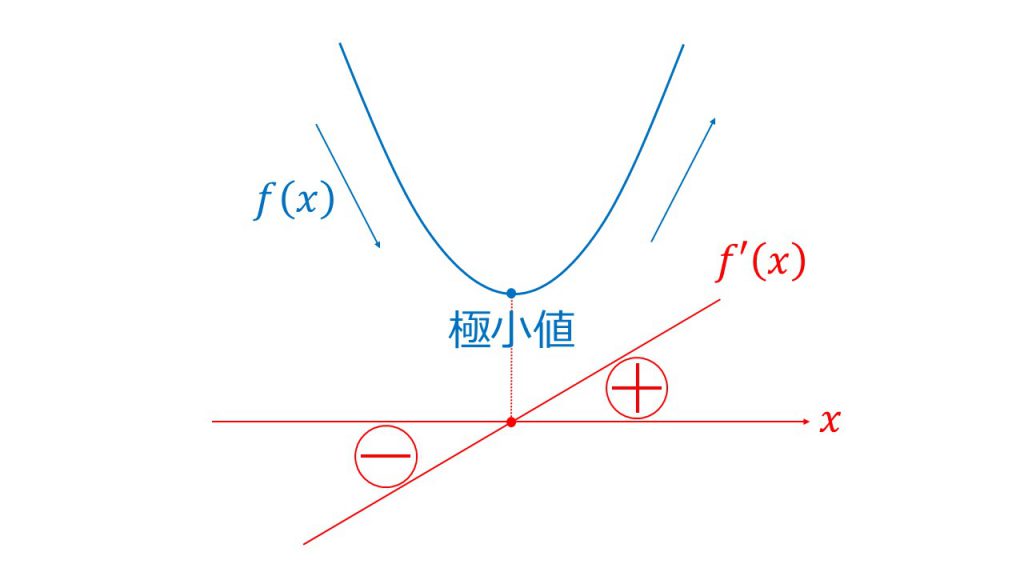
このようになっています。
元の関数が減少しているとき、導関数はマイナスとなりx軸よりも下の部分にあります。そして元の関数が増加しているときは、導関数はプラスつまりx軸よりも上にあります。
導関数が0になれば必ず極値をとるわけではない
1点だけ注意したいのは極値とは関数の増加と減少が変わる場所、つまり導関数の正負が変わる場所であり、導関数のグラフがx軸より上の部分と下の部分の両方あるということなので、極値は導関数が0になる部分ではないということになります。
例えば、
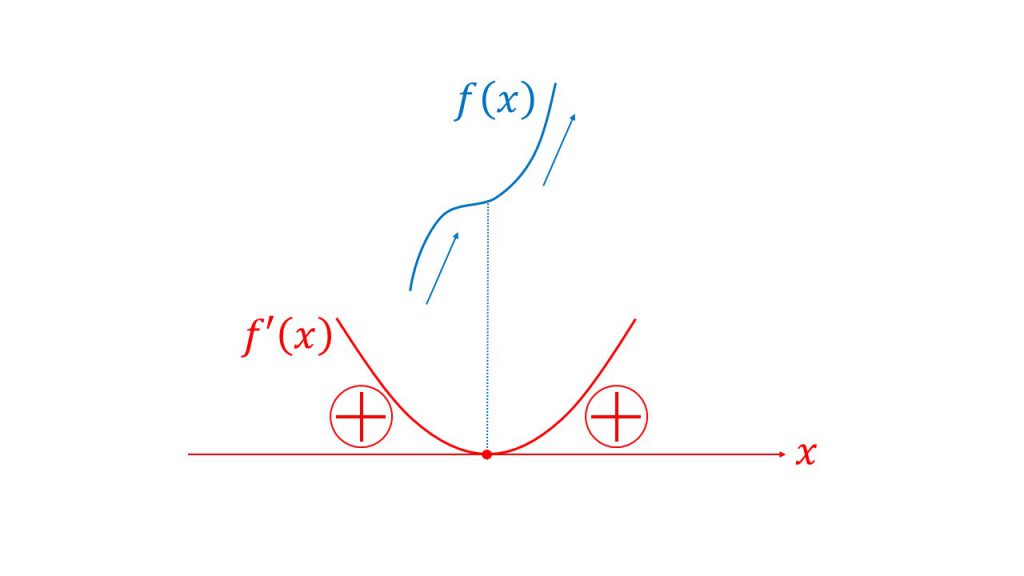
導関数がこのようになった場合、導関数は0となる瞬間があります。
しかし元のグラフを考えてみると、確かに増加も減少もしない点はあるのですが、その前後では増加から増加になっているので、この点は極値とは言いません。あくまで前後で増減が変わる場所のことを極値と言います。
3次関数が極値をもつ条件
以上より、3次関数が極値をもつ条件を考えてみると、
3次関数f(x)が極値をもつということは、導関数をf’(x)としたとき、f’(x)=0の判別式Dが0より大きくなる
ということになり、
3次関数f (x)が極値を持たないということは、f’(x)=0の判別式をDとしたとき、D≦0
となります。注意点として判別式のイコールは持たない方の条件に入るということです。
f’(x)のグラフと、それに対応するf(x)のグラフ
例えば、f’(x)=0の判別式Dが0より大きいときは、f’(x)のグラフと、それに対応した元のf(x)のグラフは以下のようになり、

増加・減少・増加となるので極値を2つ持ちます。
またD=0のときは先ほど確認したとおりこのようになります。

f’(x)=0となる場所で増加も減少もしない点は存在するのですが、増加から増加となっており極値をもつているとは言えません。
そしてD<0のときはx軸との交点を持たないということなので、導関数が下に凸の場合は常に正となり元の関数は常に増加となります。

このように極値をもつ条件を考えるときは、そもそも極値とは何かを正確に理解した上で極値をもつ条件を使えるようになりましょう。
「f’(α)=0 ⇒ f(x)がx=αで極値をとる」は偽
極値をもつ条件を、そもそも極値とは何かから正しく理解していれば、次のことも理解することができると思います。
「f(x)がx=αで極値をとる ⇒ f’(α)=0」は真
「f’(α)=0 ⇒ f(x)がx=αで極値をとる」は偽
「f(x)がx=αで極値をとるならば、f’(α)=0」これは真です。しかしその逆の、「f’(α)=0ならばf(x)がx=αで極値をとる」は偽となります。
なぜなら先ほど確認した通り、3次関数f(x)においてf’(x)=0の判別式が0となるときは導関数が0になる瞬間はあるのですが、その前後はともに増加になっているので極値を取らず、これが反例となるからです。
例題①:3次関数が極値をもつための条件
それではこれまでの解説を踏まえて2つの例題を解いてみます。
(例1)
f(x)=x3-Pxが極値をもつためのPの条件を求めよ。
(答)
f’(x)=3x2ーP
3x2ーPの判別式をDとすると
D=12P
D>0のとき、f(x)は極値をもつので
12P>0 ⇔ P>0
まずはこちらの例題です。f(x)=x3ーPxが極値をもつためのPの条件を求めてみます。
まずはf(x)を微分して導関数f’(x)を求めます。そして先ほど確認した通り、極値をもつ条件はf’(x)=0の判別式をDとしたときDが0より大きいとき、つまり12Pが0より大きいときなので、これを計算してP>0。これがこの問題の答えとなります。
ただ極値をもつための条件を問われたら、導関数=0の判別式が0より大きいときを計算すれば答えが出ます。
例題②:極値の条件から3次関数を決定する
続いてこちらの例題を解いてみます。
(例2)
f(x)=x3+px2+qxは、x=-1で極大値2をとる。このときp, qの値を求めよ。
(答)
f’(x)=3x2+2px+q
f(-1)=2より ー1+p-q=2…(ア)
f’(-1)=0より 3ー2p+q=0…(イ)
(ア)(イ)より p=0, q=-3
逆にこのとき
f(x)=x3-3x
f’(x)=3x2-3=3(x+1)(x-1)
であるので、f(x)の増減表は以下となる。
| x | … | -1 | … | 1 | … |
| f'(x) | + | 0 | − | 0 | + |
| f(x) | ↗ | 2 (極大) | ↘ | -2 (極小) | ↗ |
このときf(x)は条件を満たすので、p=0, q=-3
f(x)=x3+px2+qxがx=-1で極大値2をとるとき、p, qの値を求めてみましょう。
まずはf(x)を微分して導関数を求めます。そしてx=-1で極大値2をとるということは、x=-1のときf(x)は2であるということなので、f(-1)=2となり、またx=-1で極値をとっているので、f’(-1)=0となります。そして、この2つの式を連立させることで、pとqが求められます。
十分性の確認
しかし、ここまでで答案を終えてしまうと丸はもらえません。
ここから先の、逆の確認をしないといけません。なぜなら、ここまでで求めたものは必要条件であり、ここから先で十分条件であることを確認しないといけないからです。このことを「十分性の確認」とも言ったりします。
もう少し分かりやすく言うと、ここまでで出ているのはあくまで答えの候補が出ているだけで、ここから先でその答えの候補が問題の条件を満たしているかを確認して、それが確かに答えであることを確認しているのです。
今回の問題で言えば、f(-1)=2, f’(-1)=0という2つの条件を使ってpとqの値を出しているのですが、この2つの条件が言っていることは、あくまでf(x)はx=-1のとき2であり、f’(x)はx=-1のとき0となる、つまり、この2つの式だけではx=-1で極大値が2となるかは言えていない、ということになります。
例えば、この式を満たすだけではx=ー1で極小値2となる可能性や、あるいはx=-1では増加も減少もしないが、極値を持たない可能性もあるということになります。そのため、x=-1で極大値となることを確認しないといけないのです。
確認の仕方としては、ここまでで出た答えの候補をf (x)に代入してみて、微分をし導関数を求め、増減表をかいてみます。すると確かにx=-1で極大値にとなることが確認でき、p=0, q=-3のときf (x)は条件を満たすことが確認できたので、このp=0, q=-3は今回の問題の答えとなるということが言えます。
このように極値とは何かを正しく理解することで、これらのタイプの問題を正しく解くことができるようになります。しっかりと原理から理解するようにしましょう。
(3)解説授業の内容を復習しよう
(4)微分(数学Ⅱ)の解説一覧
②導関数とは何か(導関数と微分係数を区別しよう、導関数と関数の増減との関係、増減表の正しい作り方)
③極値をもつ条件(そもそも極値とは何か、「f'(α)=0ならばx=αで極値をもつ」は偽である理由、極値の条件から係数を決定する問題で逆の確認(十分性の確認)をしないといけない理由も解説しています)
