(1)公式を確認しよう

☆この公式の解説はこちら→階差数列の公式の原理(答案の書き方、なぜn≧2にするのか、そもそもなぜこの公式が成り立つのかについて解説しています)
(2)演習問題
☆問題のみはこちら→階差数列(数学B)をマスターしよう!(問題)
①

【答案】


- 「n≧2のとき」と記述してから公式を利用して一般項を求め、n=1のときも成り立つことを確認するという流れで答案を作る。
- 階差数列を利用した公式を使うときは、Σの上がn-1になることに注意する。
- この問題の詳しい解説はこちら→階差数列の公式の原理(答案の書き方、なぜn≧2にするのか、そもそもなぜこの公式が成り立つのかについて解説しています)
②

【答案】

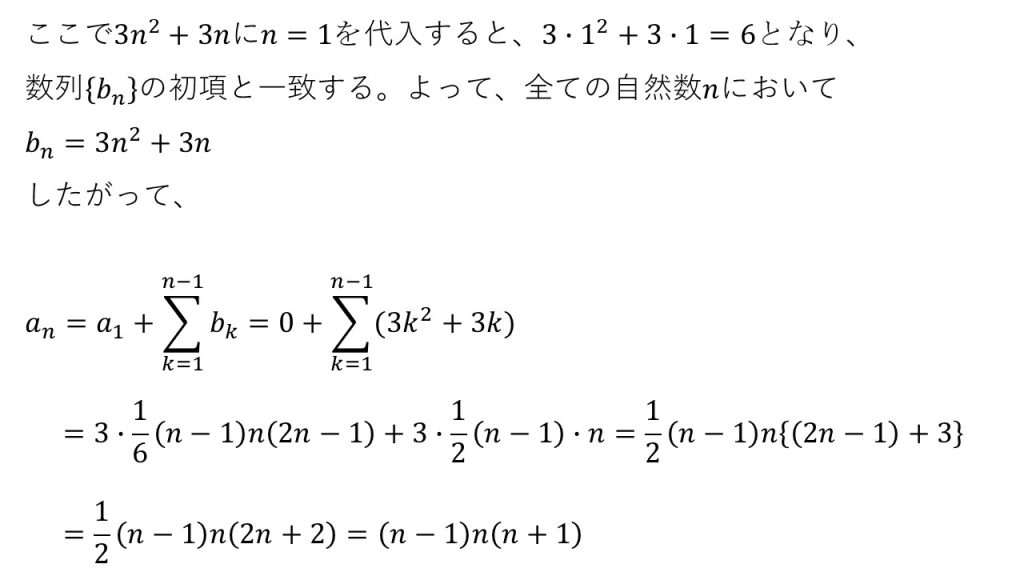

- 与えられた数列の階差数列を考えても、等差数列や等比数列になっていない場合、その階差数列の階差数列(第2階差数列という)を考えてみよう。
- 第2階差数列の一般項を求め、(第1)階差数列の一般項を求め、元の数列の一般項を求めるという手順で解く。
- Σの計算をするときは、全て展開するのではなく、まず因数分解をするようにすると計算がラクになる。
③これ以降は漸化式を利用します。
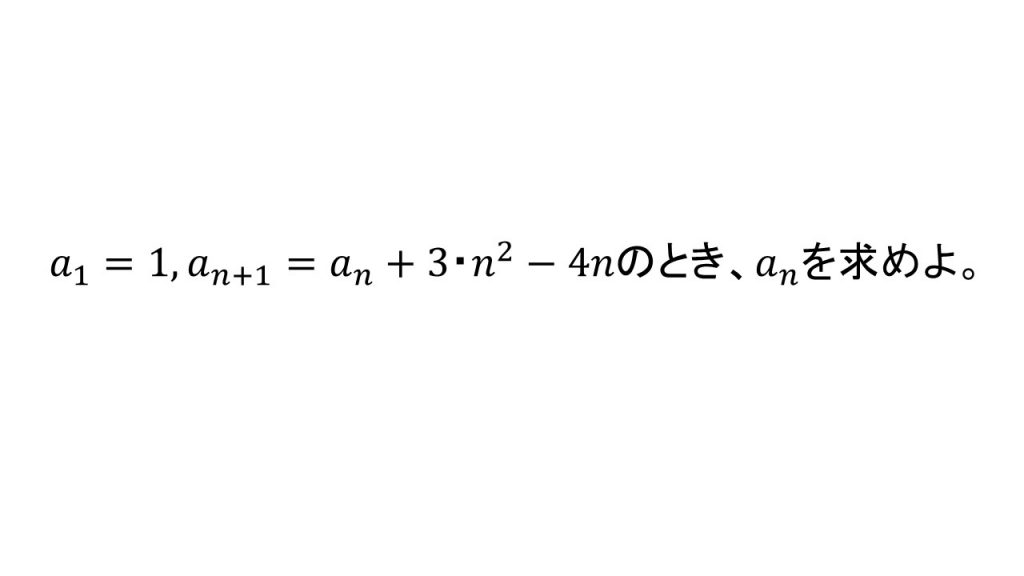
【答案】

- an+1-an=f(n)の形になっている場合f(n)はanの階差数列である。
- 詳しい解説はこちら→漸化式をマスターしよう(2)基本パターン⑦(階差数列の公式を使うパターン)
④
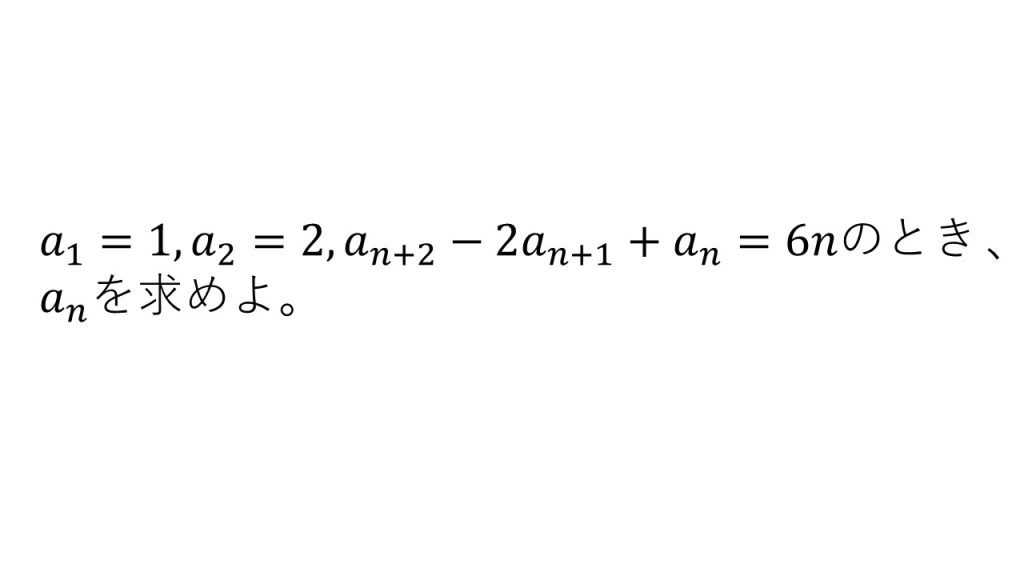
【答案】


- 6nはanの第2階差数列になっている。(6nはbnの階差数列であり、bnはanの階差数列である。)
- 詳しい解説はこちら→漸化式をマスターしよう(3)応用パターン②(式変形の発想が難しい漸化式、この漸化式が自力で解けたら漸化式マスターです)
~参考~
☆漸化式(数学B)をマスターしよう(漸化式全パターンの解説・授業・演習問題一覧)
