(1)例題
①底面積Sの円筒形のコップを密度ρの液体につけてから持ち上げたところ、図のように、コップ内外の液面の高さの差がhとなった。コップ内部の空気の圧力Pを表せ。
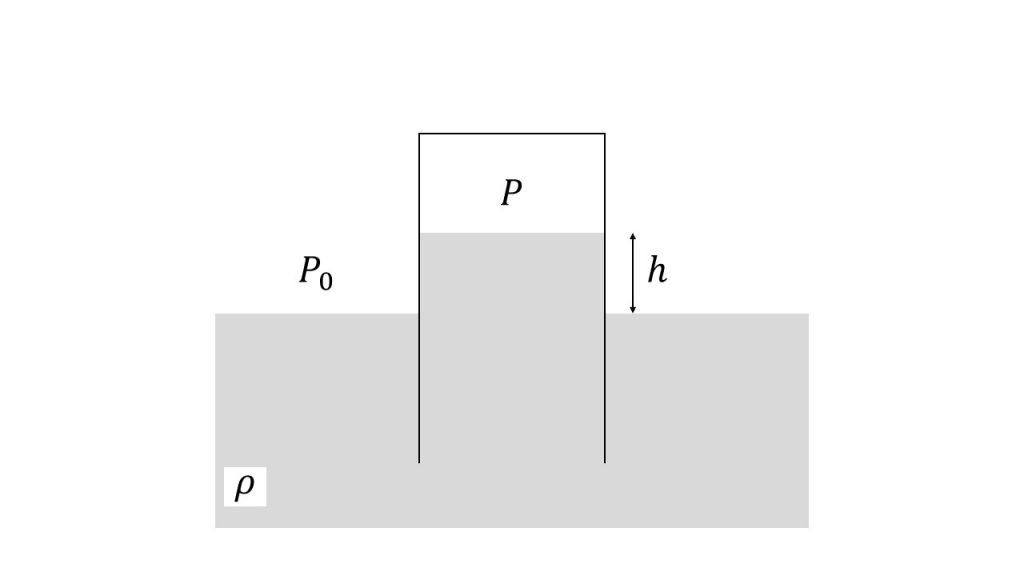
(2016年センター試験本試物理基礎第1問問3)
②J字型をした断面積一定の管があり、管の壁は熱をよく通す。大気圧P0の下で、その管に液体を注入し、下図(a)に示すように、管の上端の一方をふたでふさいだ。このとき、ふたにより閉じ込められた気体の圧力はP0、温度はT0、鉛直方向の長さはℓ0であった。この状態を状態Aとする。ただし、液体の密度をρ、重力加速度の大きさをgとする。また、液体の蒸発は無視できるとし、大気圧P0、液体の密度ρは常に一定であるとする。
1.さらに液体を注いだところ、液面が上昇し、下図(b)のように、気体部分の長さがℓ1、液面の高さの差がhになった。温度はT0のまま変わらなかった。この状態を状態Bとする。状態Bの気体の圧力P1をρ, h, g, ℓ0, ℓ1, P0から必要なものを選んで表せ。
2.P1はP0の何倍か。h, ℓ0, ℓ1から必要なものを選んで表せ。
3.しばらくして外気温が変化し、液面の高さが変わったので、高さの差が状態Bと同じhになるように液体の量を調整した。その結果、下図(c)のような状態Cになった。このとき、気体の温度は外気温と同じT1であった。状態Cの気体部分の長さを表せ。ただし、T0, T1, ℓ1を使って答えよ。
(2014年度センター試験本試験物理Ⅰ第4問Cより)
③一端を閉じた質量M、断面積Sの円筒を内部に少し空気が残るように水中に入れ、底面を上にして静かに手を離すと、下図のように、円筒中の水面が外部の水面より少し下がった状態で、鉛直に静止した。外部の大気圧をP0、水の密度をρ、重力加速度の大きさをgとする。円筒は熱を通さず、円筒の厚さは無視できるものとする。また、円筒内部の空気は、常に水温と同じ温度であるとし、その質量はMに比べて十分小さく無視できるものとする。
1.水温を測定したところ15℃であり、円筒内の気柱の高さはℓだった。その状態から、水温を43℃まで上げた。このとき、気柱の高さはℓの何倍になるか。有効数字2桁で答えよ。ただし、外部の大気圧はP0、水の密度はρのままであるとし、水の蒸発は考えないものとする。
2.次に下図のように円筒を鉛直に保ったまま引き上げると、円筒の水面は外部の水面からhの高さまで上がった。このとき、手が円筒を上向きに支えている力の大きさを求めよ。
(2011年度センター試験本試験物理Ⅰ第4問Cより)
(2)例題の答案
①圧力による答案
コップ内の空気と水の境目における圧力のつりあいより、水深の基準をコップ外の液面とすると
P=P0+ρ(-h)g=P0-ρhg
①力のつりあいによる答案
コップ外の液面よりも上の部分のコップ内の水を一つの物体と考える。この物体における力のつりあいの式は、コップ外の液面における水圧がP0であるので
PS+ρShg=P0S
∴ P=P0-ρhg
②-1

②-2

②-3

③-1

※円筒内の気体の体積は変わるが、円筒内の液面の位置は温度を変えても変わらないということである(水圧が変わらない⇒水深も変わらない)
③-2

(3)解法のポイント
まず、最も重要なポイントは、圧力と力を区別することです。
②は圧力のつり合いで考え、②は力のつり合いで考えます。
②圧力のつり合いを考えるときは、液面(壁)での圧力のつり合い(下から押す圧力と上から押す圧力のつり合いを考えます)
その際、水の中では、水圧と大気圧の両方がかかることに注意しましょう。
また、水圧は水深に比例します。水深の基準は、大気圧によってつり合っている液面を基準とします(③では基準よりも上なので、水深が負の値になる)
③力のつり合いを考えるときは、浮力を導入します。
浮力とは、流体内で物体を
(下から押し上げる力)-(上から押さえつける力)
であるという定義通りに扱いましょう。
浮力を考えているときは水圧を式に入れてはいけません。
このように、圧力と力を区別し、水圧と浮力は定義通りに扱うことを徹底することで、このパターンの問題は正確に解くことができます。
※ボイルの法則・シャルルの法則・ボイルシャルルの法則を使う問題は、どれを使うのか判断するのが面倒なときは、すべて状態方程式で立式して、辺々を割るというやり方で解いても構いません。
(4)必要な知識
①圧力

②浮力

③ボイルの法則

④シャルルの法則

⑤ボイル・シャルルの法則

⑥理想気体の状態方程式

(5)理解すべきコア
①浮力・水圧の定義について確認しましょう→浮力とは何か(水圧と浮力の違い、アルキメデスの原理についても解説しています)
②圧力のつり合いの考え方を確認しましょう→流体内(大気中・水中)の圧力を考えるときのポイント(圧力はあらゆる方向からかかる、圧力のつり合いは壁で考える、力のつり合いと圧力のつり合いの違い)
③理想気体の状態方程式の使い方と計算の工夫の仕方を確認しましょう→理想気体の状態方程式の使い方解説動画(理想気体とは何か、混合気体の考え方、計算の工夫の仕方についても解説しています)
