①最大・最小を考えるときに縦に引く3つの線
→二次関数の最大と最小を考えるときに引くべき3つの線解説授業
ⅰ)定義域
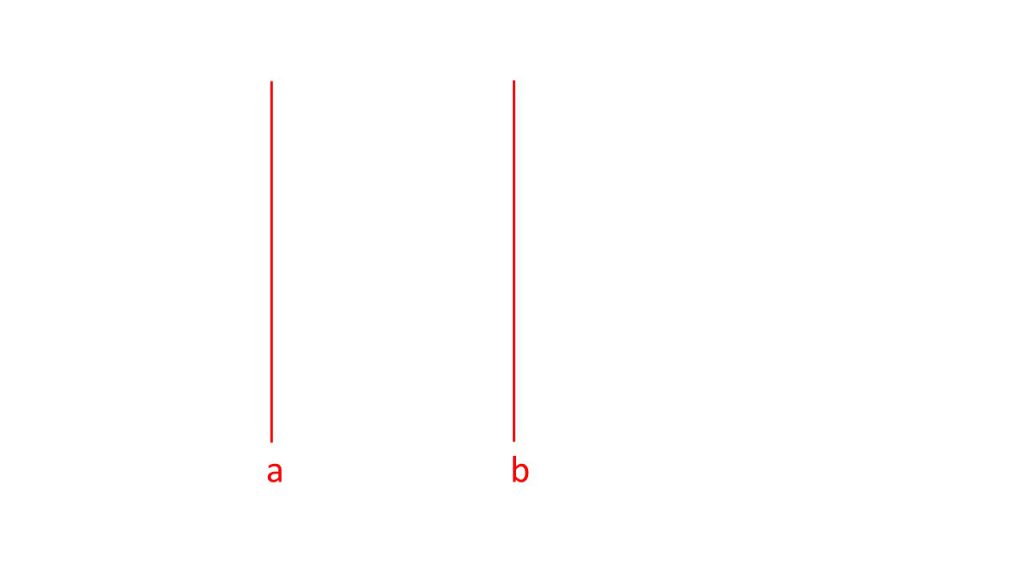
ⅱ)定義域の中央
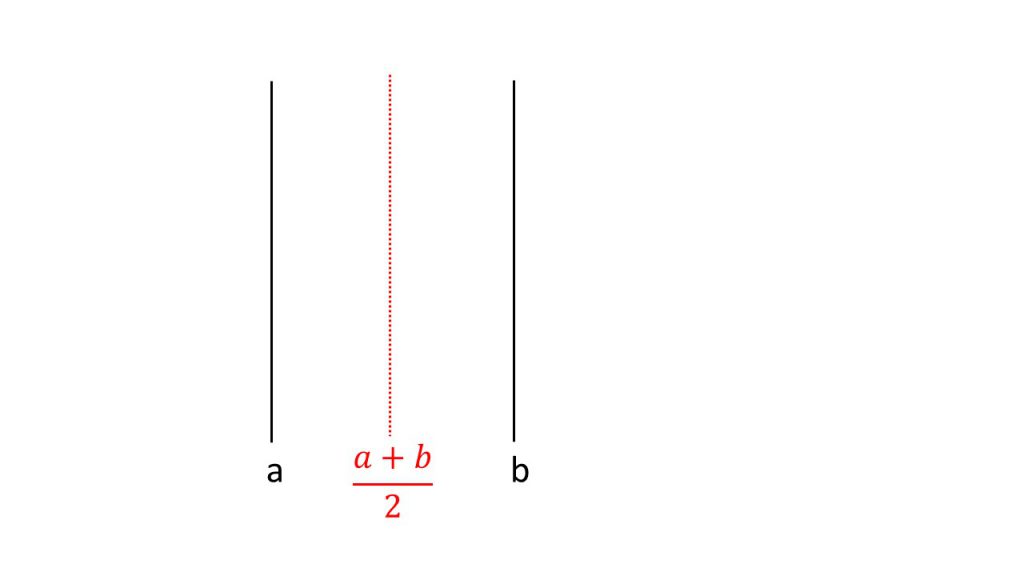
ⅲ)軸
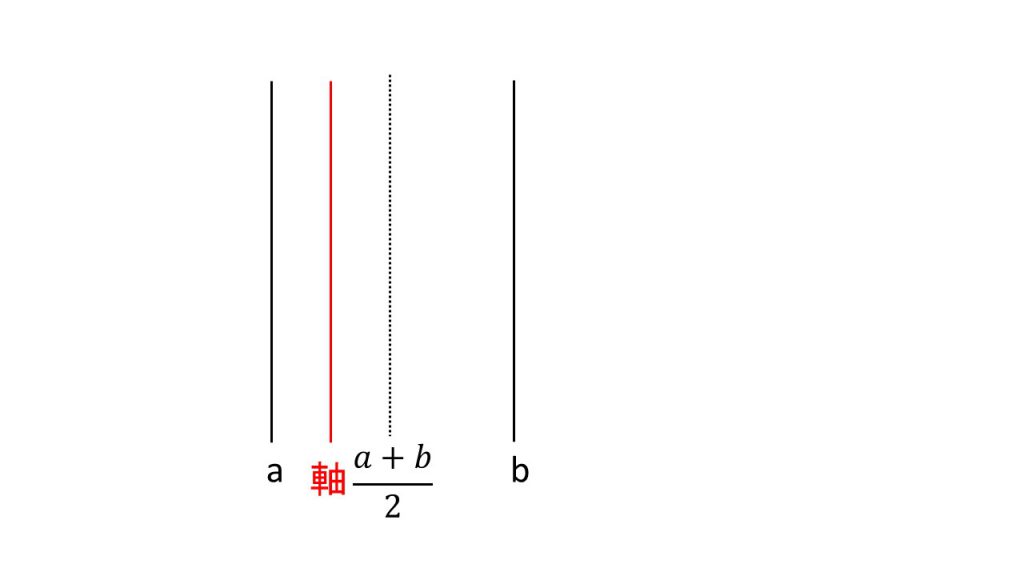
→ⅰ)~ⅲ)を引いた後、放物線をかけば、どこが最大・最小か分かるようになる。
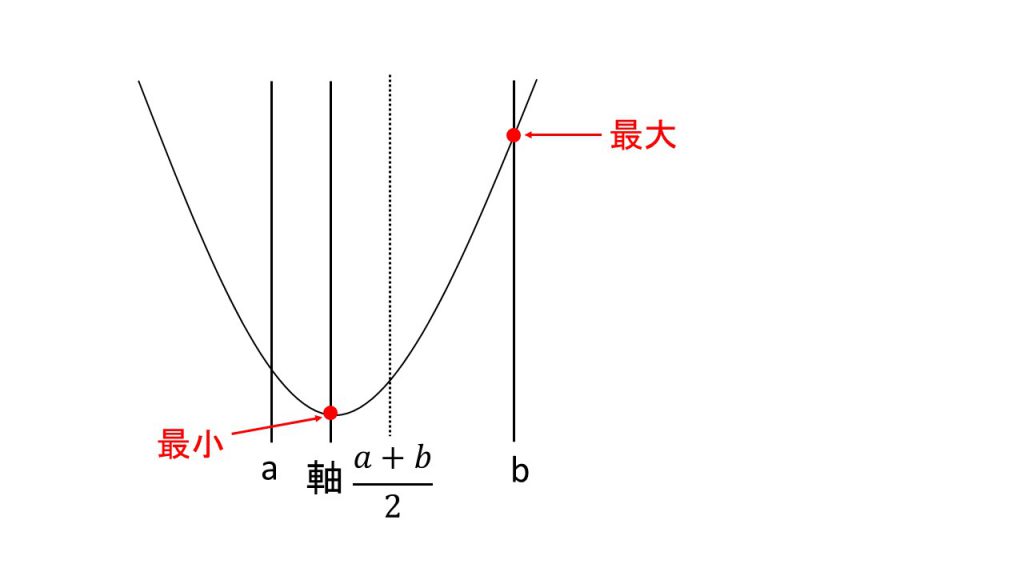
→二次関数の最大と最小を考えるときに引くべき3つの線解説授業
②場合分け
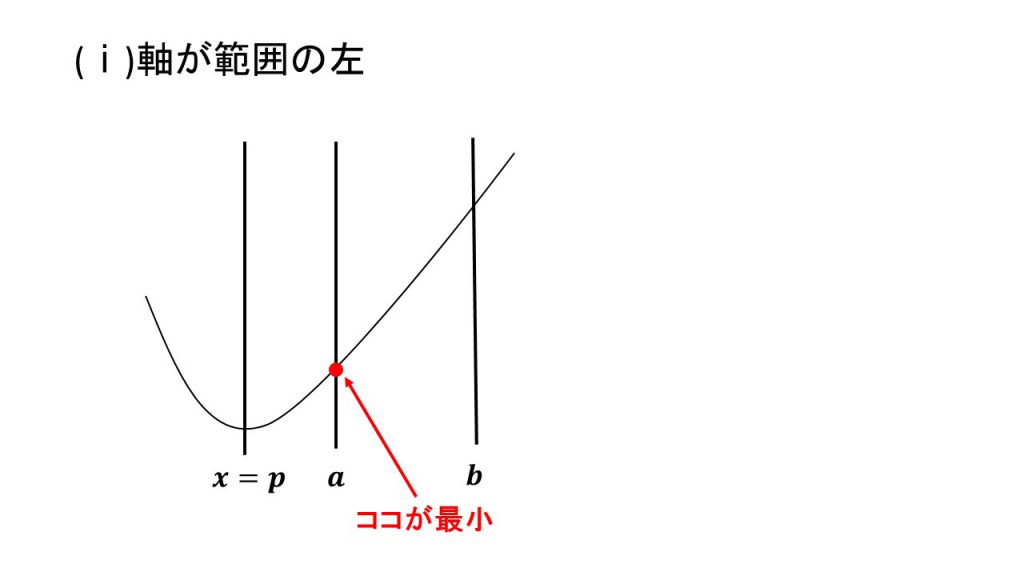
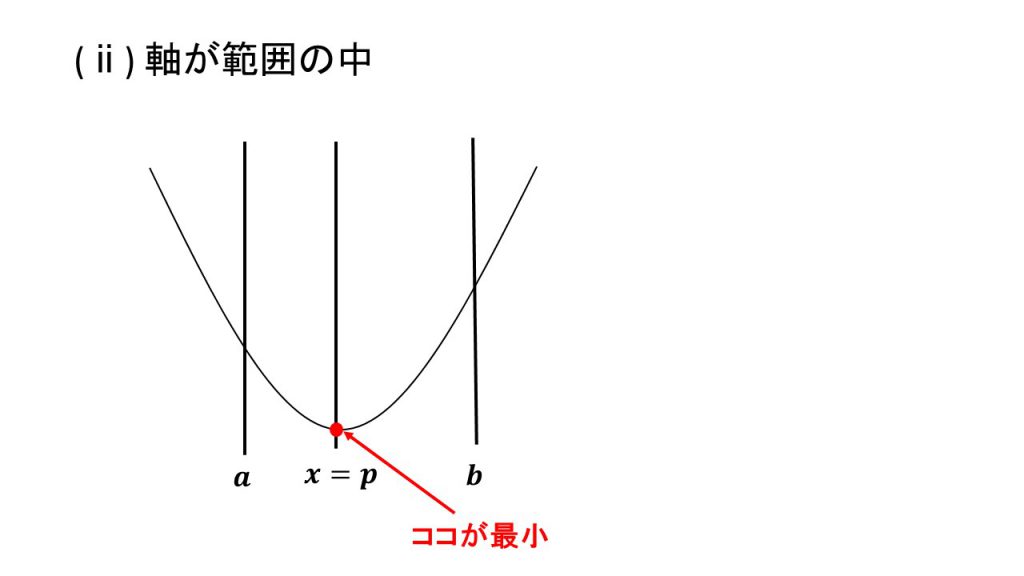
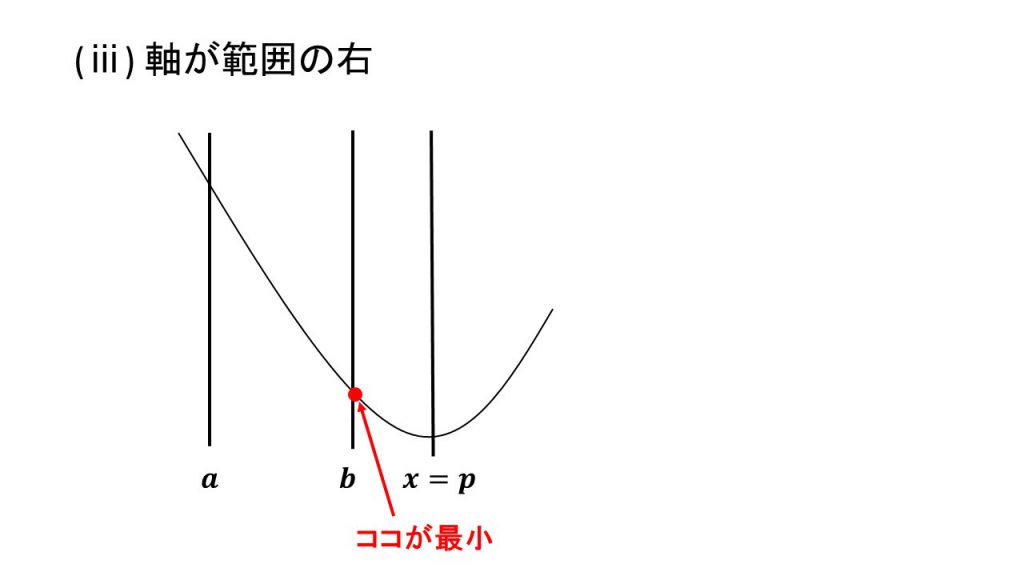
1.下に凸で最小値
ⅰ)軸が範囲の左、ⅱ)軸が範囲の中、ⅲ)軸が範囲の右
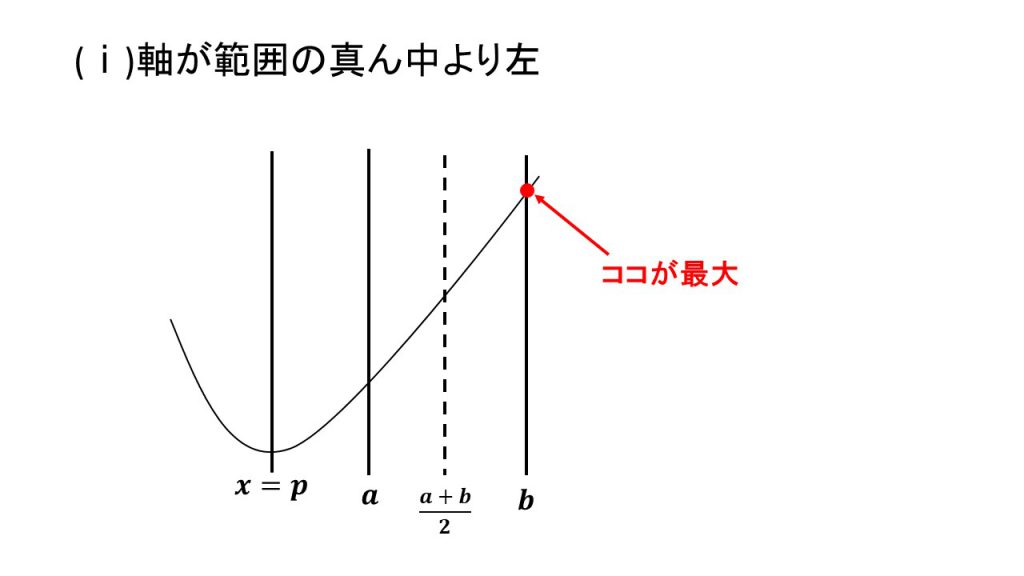
2.下に凸で最大値
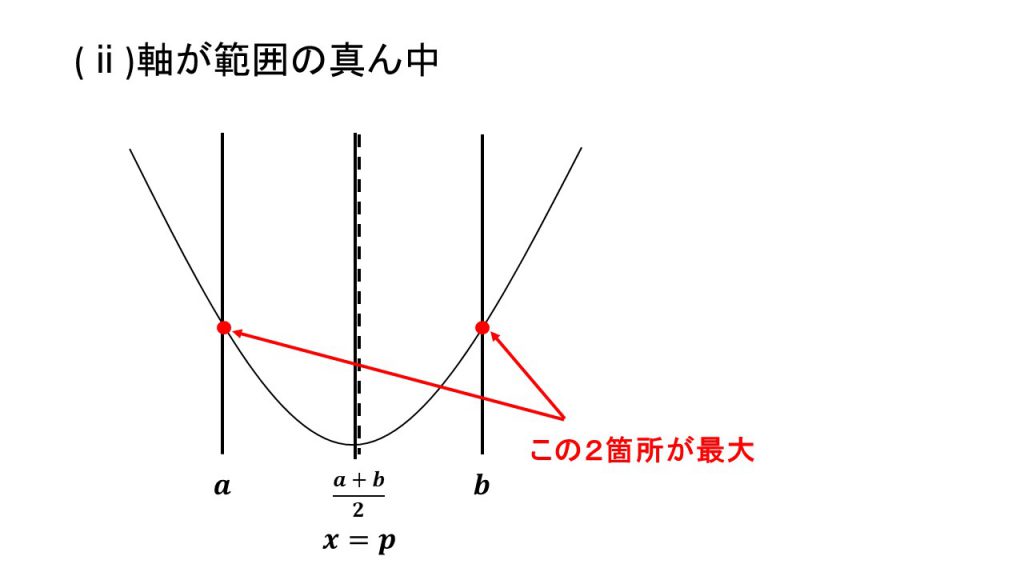
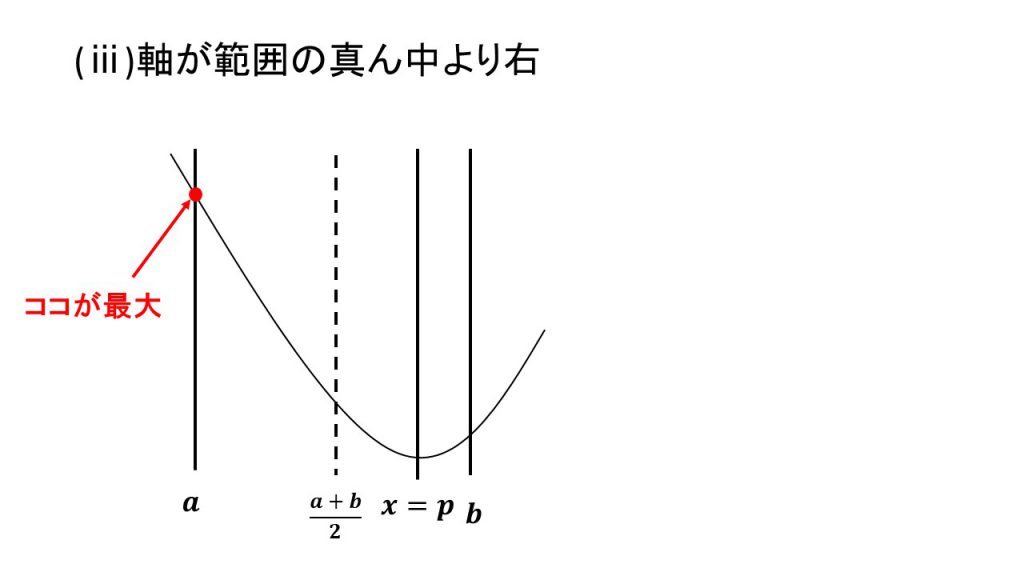
ⅰ)軸が範囲の真ん中より左、ⅱ)軸が範囲の真ん中と一致、ⅲ)軸が範囲の真ん中より右
3.上に凸で最小値
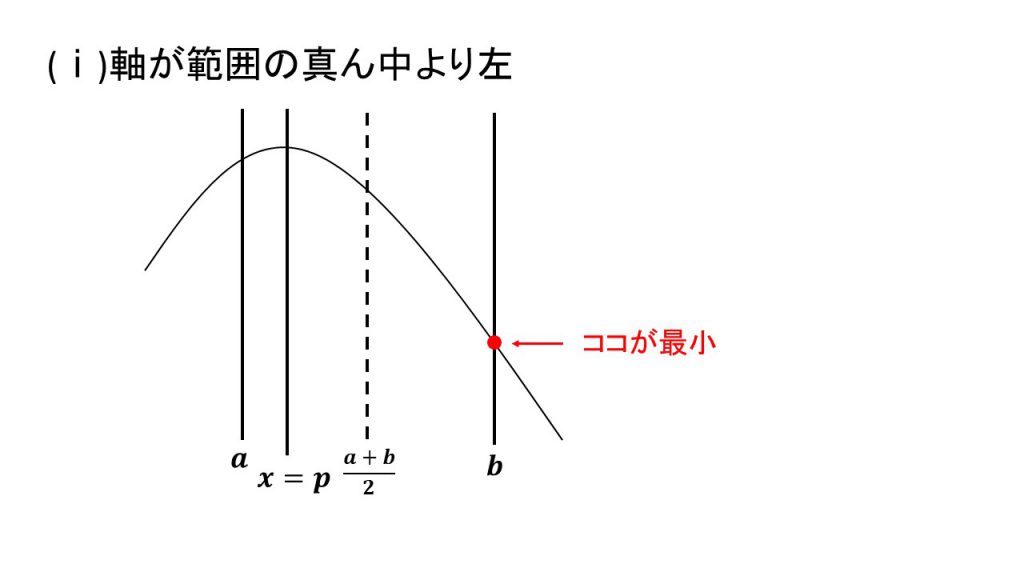
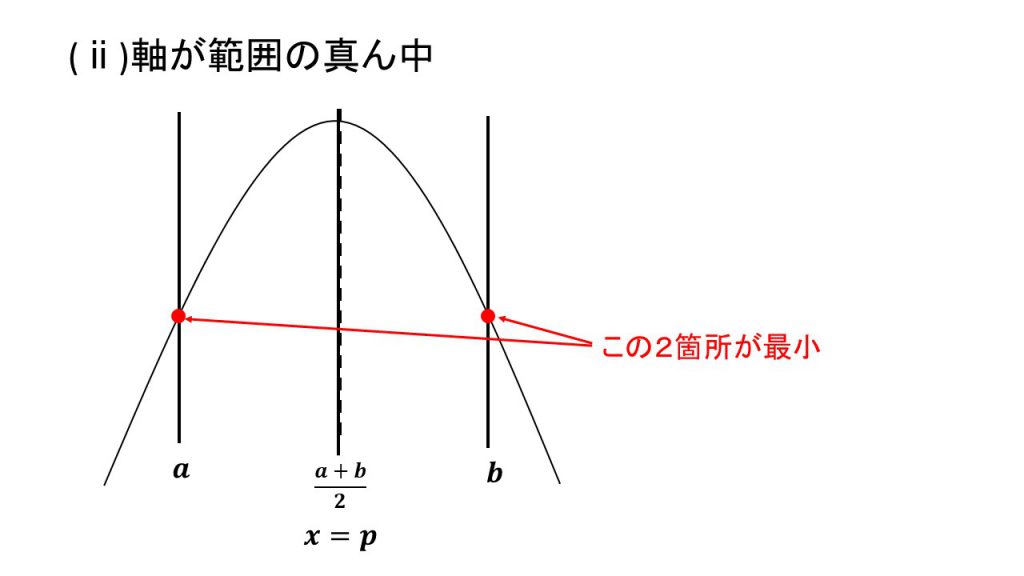
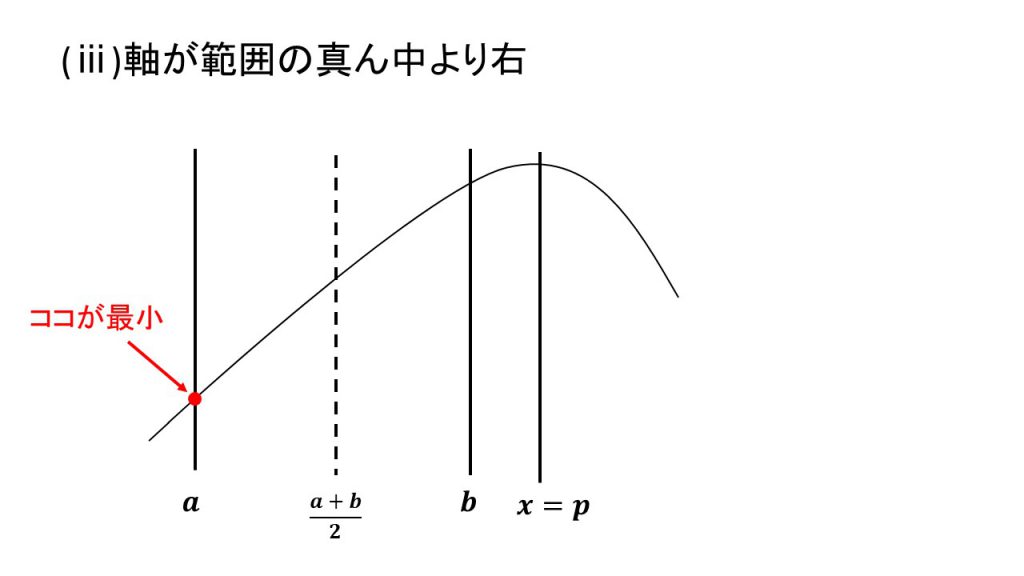
ⅰ)軸が範囲の真ん中より左、ⅱ)軸が範囲の真ん中と一致、ⅲ)軸が範囲の真ん中より右
4.上に凸で最大値
ⅰ)軸が範囲の左、ⅱ)軸が範囲の中、ⅲ)軸が範囲の右
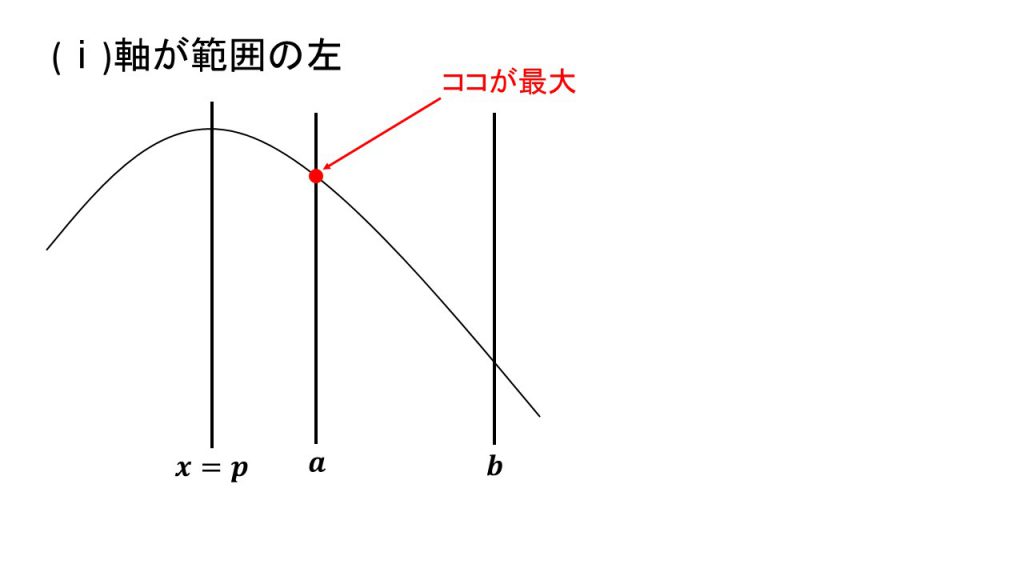
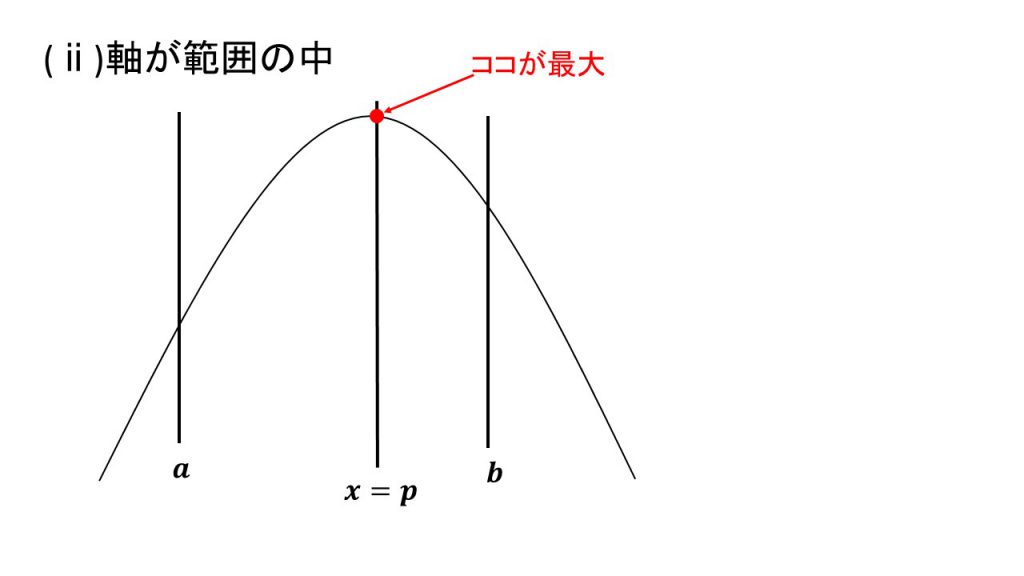
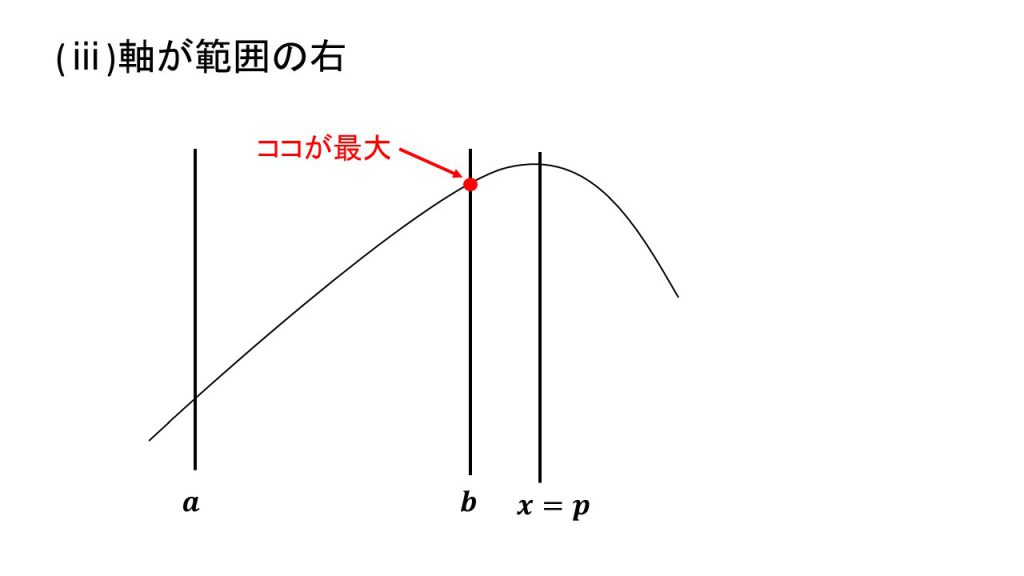
これらの場合分けの4パターンは覚えるというよりは、実際に3つの線と放物線をかいてみて理解するとよいでしょう。
③二次関数の決定で使う3つの式

④二次方程式の解の公式と判別式
-1024x576.jpg)
ⅰ)判別式が正のとき、異なる実数解が2つ
ⅱ)判別式が0のとき、実数解が1つ(重解)
ⅲ)判別式が負のとき、実数解はない(異なる虚数解が2つ)
⑤二次不等式の解法
ⅰ)左辺を因数分解できるときは因数分解する。因数分解できないときは、左辺=0の方程式を解の公式を利用して解く。
ⅱ)y=(左辺)のグラフがx軸よりも上か下かを考える。
⑥二次関数のグラフとx軸の交点の位置の問題で考えるべき3つの条件
ⅰ)判別式
ⅱ)軸
ⅲ)端点のy座標
【数学Ⅰ公式一覧】
②数の分類一覧(複素数、実数、有理数、無理数、整数、自然数、素数)
~参考~
☆二次関数・二次方程式・二次不等式(数学Ⅰ)の解説・授業・公式・演習問題一覧
