(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
向心力によって円運動が生じている
まず確認しておきたいのが、「向心力によって円運動が生じている」ということです。よく「円運動をすることによって向心力が発生する」と勘違いしている人がいますが、これは間違いなので注意してください。
例を使って確認してみます。例えば水平面上に釘を打ち、その釘と物体を糸でつなぎます。そしてその物体を糸と垂直な方向に速度vを与えたら、その物体は円を描いて運動します。
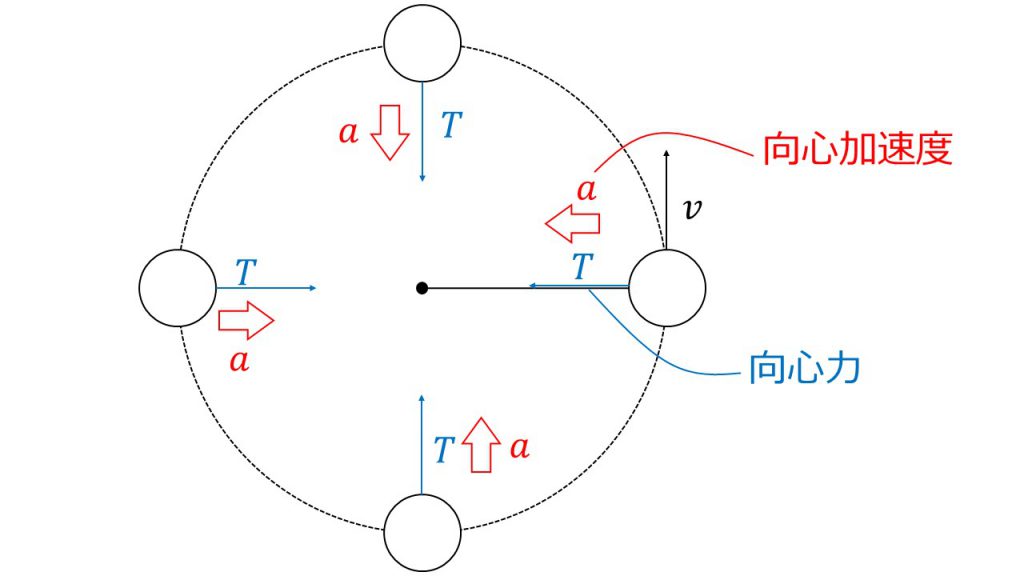
それはなぜかというと、物体には常に中心方向に糸の張力がはたらくからです。つまり、運動方程式から「Fベクトル=maベクトル」が成り立っており、張力Tの方向に加速度が生じるので、物体には常に中心方向の加速度が生じていることになります。
そのため、円の接線方向に移動としようとしても、中心方向の加速度が生じているため、少し内側に移動し、そしてまた接線方向に移動しようとしても中心向きの加速度が生じているので少し内側に移動し……それを繰り返して円運動となるのです。
このように、円運動を成り立たせている中心方向の力のことを向心力とよんでおり、その向心力によって生じた加速度のことを向心加速度とよんでいます。
したがって、向心力となる中心方向の力があるので中心方向の加速度が生じ、物体が円運動をすることができるのです。
遠心力とは見かけの力
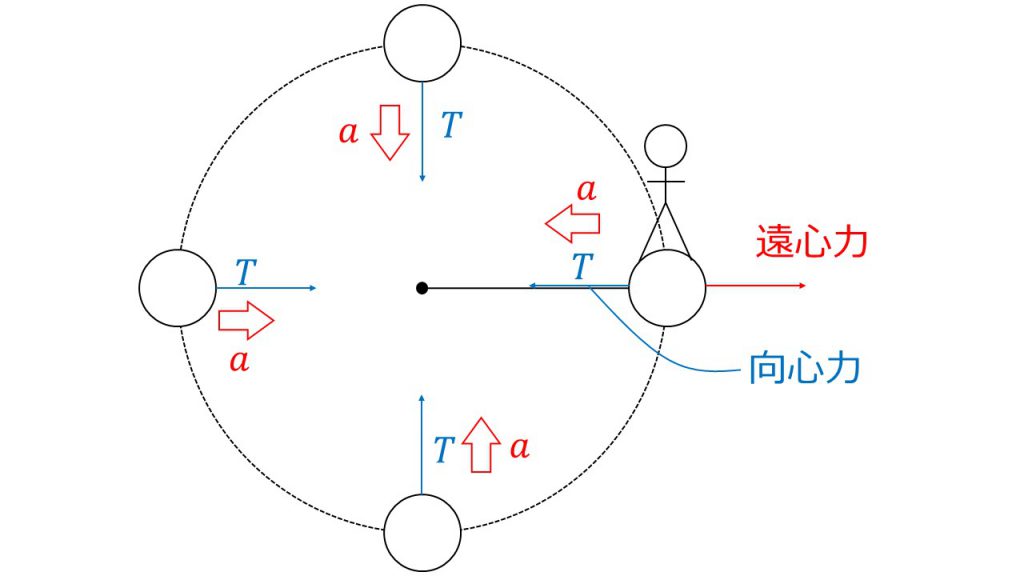
また、遠心力についても確認します。遠心力とは、観測者が物体と同じように円運動をしているときに、中心方向から外向きに生じていると感じる見かけの力のことです。
見かけの力とは、円運動の外から見ている人にとっては観測できないけど、一緒に円運動している人にだけあると感じる力のことであり、つまり遠心力=慣性力なのです。慣性力は、加速している観測者が加速度と逆向きにあると感じる力のことです。
円運動の場合は、常に中心に向かう向きに向心加速度が生じているので、一緒に円運動している観測者にとっては、その向心加速度と逆向きの慣性力つまり遠心力を感じているのです。
ちなみに、慣性力の大きさはmaとなるので、向心加速度に物体の質量をかけたものが遠心力の大きさとなります。
円運動における2つの解法
それでは円運動における2つの解法を解説します。
①まず、1つ目の解法は、「観測者が一緒に円運動をしないとした場合は、運動方程式を立てる」というものです。
そして2つ目の解法は、「観測者が一緒に円運動をするとした場合は、慣性力である遠心力を導入してつり合いの式を立てる」というものです。
この2つの解法は結局同じ式ができるので、どちらで解いても構いません。やりやすい方で解くようにしましょう。
実際に例で確認してみます。
ちなみに等速円運動の向心加速度はa=rω2=v2/rであるということは知っている前提で話を進めます。
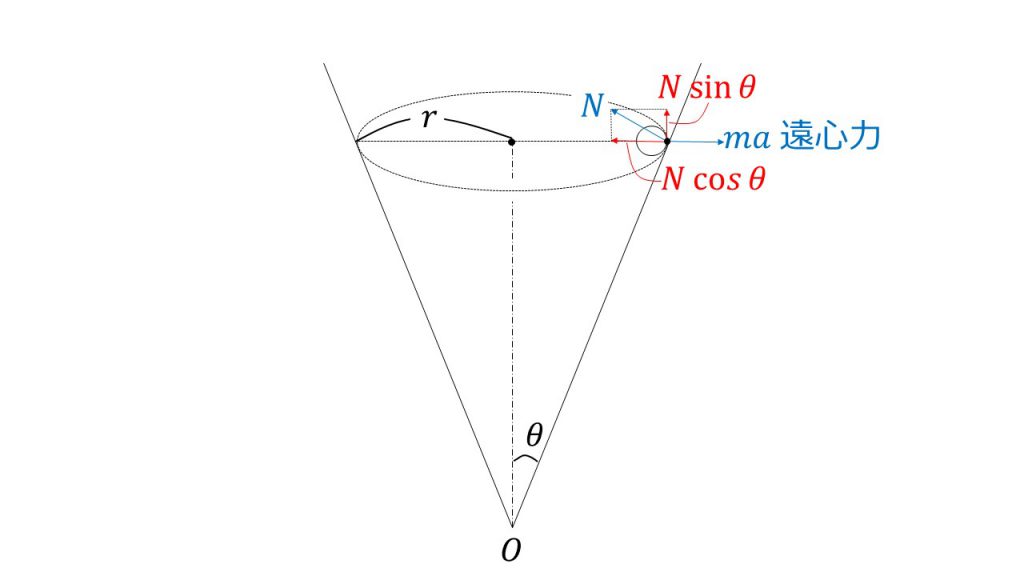
例えばこのように円錐の中で物体が等速円運動をしている場合、どのような式が立てられるか考えてみましょう。
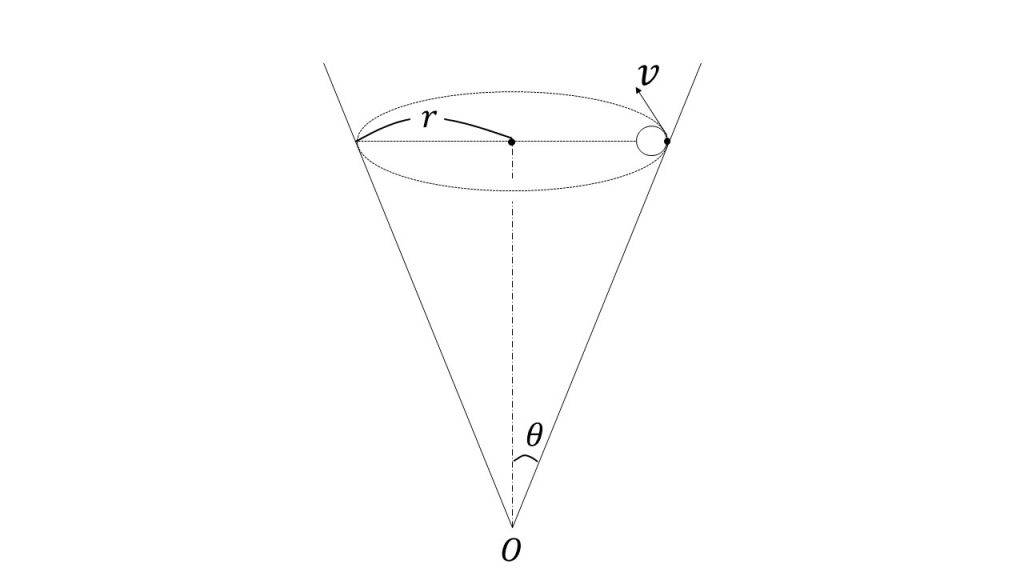
物体は速度vで等速円運動をしており、その半径をrとします。また、円錐面と中心軸のなす角をθとします。
①の解法
まずは観測者が一緒に円運動をしない場合を考えてみます。
観測者は外から見ているので当然物体は円運動をしています。そのため、円運動を成立させている向心力があるということになります。
1番目の解法で取り組む場合は、まず向心力となっている力を考えなければいけません。今回の等速円運動の向心力は、物体が円錐面から受けている垂直抗力の水平方向の分力が向心力となります。
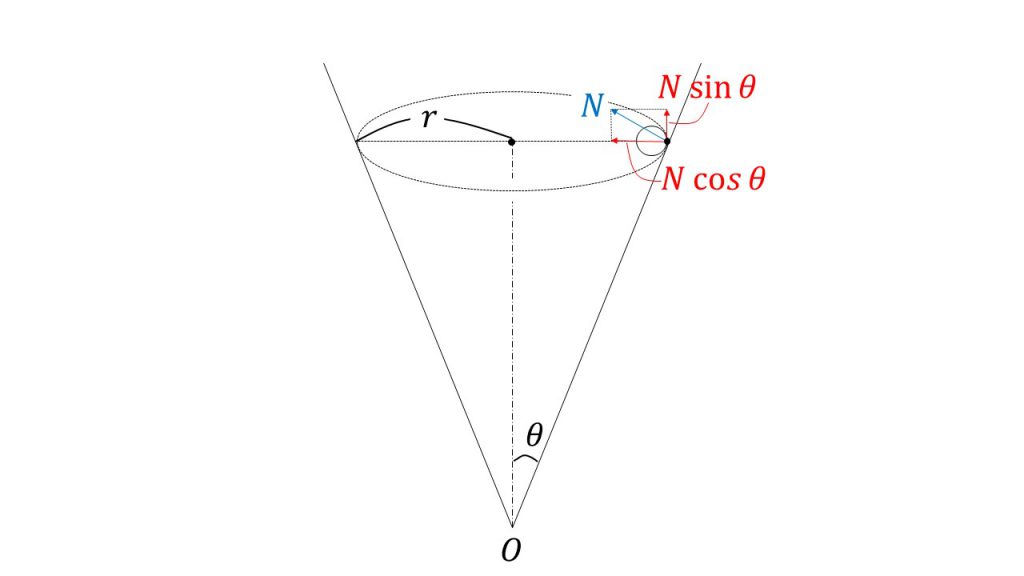
そのため、運動方程式(ma=F)より
m・v2/r=Ncosθ
という運動方程式を立てることができます。あとは鉛直方向のつり合いの式を立てて
Nsinθ=mg
この2つの式を使えば問題を解くことができます。
②の解法
それでは次に2番目の解法として、一緒に円運動をした場合どのような式が立てられるか考えてみましょう。
観測者が一緒に円運動をした場合、観測者は慣性力である遠心力を感じます。そのため、一緒に円運動をする場合は、加速度の向きと逆向きの遠心力を導入して考えることができます。
物体と一緒に等速円運動をしている場合、観測者から物体を見ると物体は静止しているように見えます。そのため、水平方向でも鉛直方向でもつり合いの式を立てることができ、水平方向では
Ncosθ=maつまりNcosθ=m・v2/r
というつり合いの式を立てることができます。
また、鉛直方向において、垂直抗力の鉛直方向の分力=重力のつり合いの式も立てることができます。
Nsinθ=mg
このようにどちらの考え方で問題に取り組んでも、結局同じ式ができます。しかし、前提となる条件や式の考え方は違うので、しっかりと区別してどちらの解法で取り組んでいるのか意識しながら問題を解くようにしてください。
(3)解説授業の内容を復習しよう
(4)円運動(力学)の解説一覧
②等速円運動の2つの解法(向心力と遠心力についても解説しています)
③等速円運動の速度と加速度をベクトルと微分を使って導く(合成関数の微分を使っています)
(5)参考
☆物理の解説動画・授業動画一覧(力学・熱力学・波動・電磁気・原子)
☆物理に関する現象や技術(力学、熱力学、波動、電磁気、原子)
