(1)例題

(2015年センター試験本試数学ⅡB第1問〔2〕(2)より)
(2)例題の答案
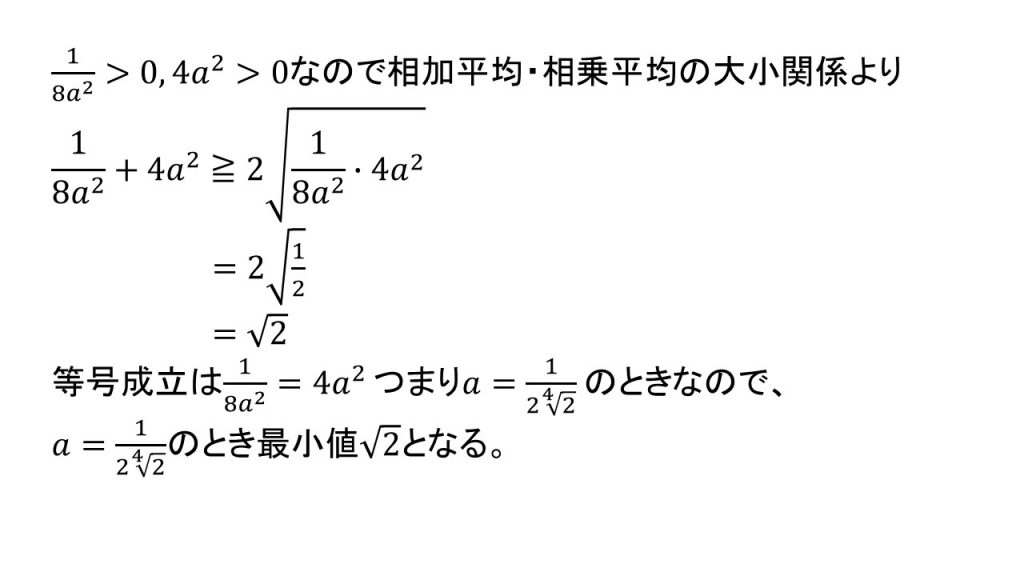
(3)解法のポイント
分母に文字が含まれている分数を含む式の最大や最小を求める問題は相加平均・相乗平均の大小関係を利用します。
相加平均・相乗平均の大小関係を利用するのは、
足し算だと上手くいきそうにないけど掛け算なら上手くいくとき
です。つまり、
分母に文字があるとき
は、相加平均・相乗平均の大小関係を考えてみましょう。
さて、相加平均・相乗平均の大小関係ですが、大切なことは3つの要素を全て使いこなすことです。
①a>0、b>0のとき、
②a+b≧2√ab
③等号成立は、a=bのとき
この3つです。
②の式しか使えない人が多いですが、①も③も重要です。
今回のような問題での使い方ですが、
①a,bに相当するものがともに正であることを確認する
②a+b≧2√abの式を立て、右辺を整理する
③a+b≧2√abということは、a+bの最小値は2√abということになる。つまり、その最小値を与えるa,bは等号成立条件のa=bを満たすとき、ということになる。
といった流れになります。
(4)必要な知識
①相加平均・相乗平均の大小関係

※(a+b)/2のことを相加平均、√abのことを相乗平均という。
(5)理解すべきこと
相加相乗平均の使い方と使いどころを理解しましょう→相加平均・相乗平均の大小関係の使い方と使いどころ(どのようなときに相加相乗平均を使うのか)
☆動画はこちら↓
