(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
今回は化学における濃度計算の基本について解説します。
実際に問題を解いていきたいのですが、その前にいくつかポイントを確認します。
高校化学で出てくる濃度3つ
まずは化学に出てくる濃度を3つ確認します。化学では主に以下の3つの濃度を使います。
ⅰ)1つ目は質量パーセント濃度で、単位は%です。
ⅱ)2つ目はモル濃度で、単位はmol/Lです。
ⅲ)3つ目は質量モル濃度で、単位はmol/kgです。
①質量パーセント濃度
質量パーセント濃度は、溶質の質量[g]/溶液の質量[g]×100で求めることができます。単位は分母と分子どちらもgになっていることに注意しましょう。
また質量パーセント濃度は実際に使うときは、以下のように使うことが多いということは知っておきましょう。
「質量パーセント濃度をaとしたとき、溶液の質量にa/100をかけることで溶質の質量となる」
このように質量パーセント濃度は、溶液の質量を溶質の質量に変換するときによく使います。
②モル濃度
続いてモル濃度ですが、モル濃度は、溶質の物質量[mol]/溶液の体積[L]となります。単位は、分母がLで分子がmolになっていることに注意しましょう。
③質量モル濃度
そして3つ目の質量モル濃度は、溶質の物質量[mol]/溶媒の質量[kg]です。分母が溶媒になっていることに注意しましょう。ただ質量モル濃度は凝固点降下や沸点上昇などを計算するときにしか使えません。
そのため化学基礎では出てこないので、今回の計算では質量モル濃度は使わず、質量パーセント濃度とモル濃度を扱った計算を解説します
濃度の計算で気をつけること3つ
続いて濃度の計算で気をつけることを3つ確認します。
①単位に注意して分母と分子と順番に考える
まず1つ目は「単位に注意して分母と分子と順番に考える」ということです。
化学に限らず、理科の計算ではとにかく単位が重要です。問題文で与えられているものの単位をよく見て、求めたい単位に変換していきます。
また分母と分子を順番に考えることで正確に式をつくることができます。
②溶質の物質量で方程式を立てる
2つ目の気をつけるポイントは、「溶質の物質量で方程式を立てる」という方針も考えてみることです。
例えば、ある溶液に水を追加したとしても、変化するのは溶媒と溶液の量であり、溶質は変化しません。そのため溶質の量が変化しない状況であれば、とりあえず溶質の物質量つまりモルを出してみて、方程式をつくることを考えてみてください。
③溶質、溶媒、溶液をメモすること
そして3つ目の気をつけることは、「溶質、溶媒、溶液をメモすること」です。
濃度の計算を苦手とする人の多くは、問題文で与えられている量や計算で出てきた値が、溶質のものなのか溶媒のものなのか溶液のものなのかを正確に区別できていません。この3つをしっかり区別することが濃度計算攻略の鍵となります。
そこで、溶質なら「し」、溶媒なら「ば」、溶液なら「え」といった記号をメモしながら計算することをオススメします。
それではこれらのポイントを意識しながら実際に濃度の計算をしてみましょう。
問題①:塩酸のモル濃度を求める
それではまず以下の問題を解いてみます。
標準状態で体積が5.6Lの塩化水素を水に溶かして、全体を100mLにします。そしてその塩酸のモル濃度つまりmol/Lを求めてみましょう。
まずは問題文で与えられている情報の整理をします。
5.6Lの塩化水素は水に溶かすものなので溶質の情報です。そして、「全体を100mLにした」とあるのでこの100mLは溶液の情報です。
分母と分子を順番に考える
ここまで確認したら式をつくっていきます。
求めるモル濃度をc[mol/L]とおき、分母と分子を順番に考えていきます。
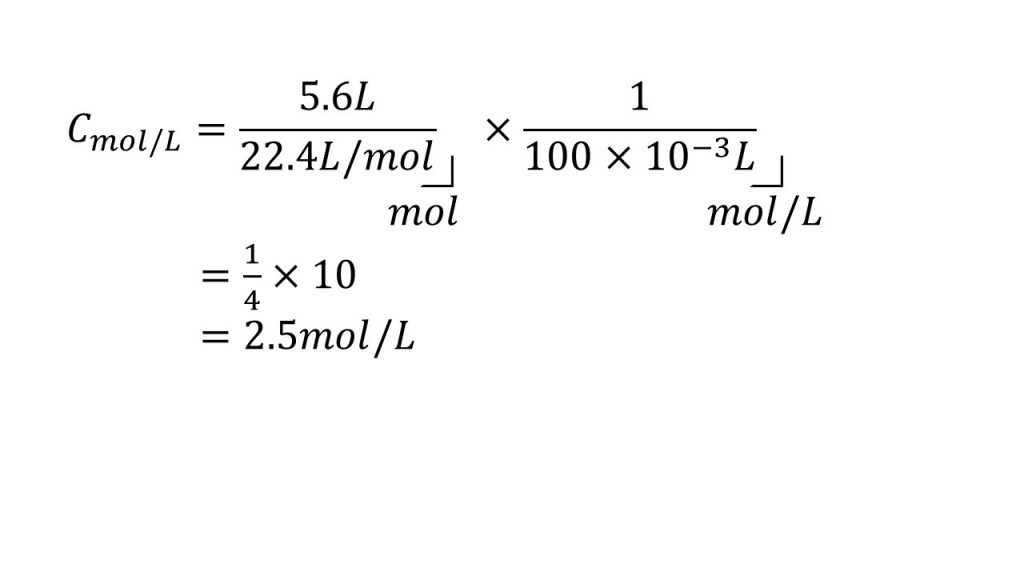
まず分母には溶液の体積がきます。
今回問題文で与えられている溶液の体積は100mLです。そのため分母には100×10-3がきます。mLを10-3倍、つまり1/1000倍することでLとなります。
分母の部分を0.1や100/1000としてもいいのですが、高校生であればなるべく10-3という書き方に慣れておきましょう。少数や分数でも間違いではないのですが、あまり少数や分数を増やしてしまうと計算ミスの原因となってしまうので、なるべく指数を使って表すようにしましょう。
それでは次に分子です。
分子は溶質のモルを求めます。問題文で溶質について与えられている情報は、体積が5.6Lということです。これをモルにするためには、塩化水素は標準状態で気体なので、体積の5.6Lを22.4L/molで割ります。
これで、分子が溶質のモルとなり、分母と分子で必要なものが揃ったので、あとは計算をしていきます。
工夫しながら計算する
今回のように分数の中に分数がある場合は、まずひとつの分数にします。またその際、分母の10-3を、分子に103として書くようにすると、計算がやりやすくなります。
次にできるだけ約分をします。まず、103と100を約分して10にします。そして22.4と5.6を約分して1/4とします。すると10/4が残るので、暗算で答えが2.5mol/Lとなります。
このように丁寧に単位と溶質 溶媒 溶液のメモを書くようにすれば、正確に計算することができます。
溶質の物質量で方程式を立てる
また「溶質の物質量で方程式を立てる」という方針で、式を作るとすると以下のようになります。
5.6[L]/22.4[L/mol]=c[mol/L]×100×10-3[L]
左辺は5.6/22.4で溶質のモルとなっており、右辺はモル濃度に溶液のリットルをかけることで溶質のモルとなっています。
このように溶質のモルで方程式を立てることもできます。
もちろんどちらで解いても答えは同じものになるので、式を立てやすい方、あるいは計算しやすい方で解くようにしましょう。
問題②:水で薄めて濃度を変えていく問題
それでは次にこのような問題を解いてみます。
6.0mol/Lの濃硫酸を水で薄めて、0.30mol/Lの硫酸を500mLつくるには元の硫酸は何mL必要でしょうか。
今回問題文で与えられている情報は、求めるものも含めてすべて溶液の情報です。
この問題のように水で薄めて濃度を変えていく問題は、溶質の物質量で方程式を立てて解くと解きやくすくなります。
なぜなら薄める前と薄めた後で濃度と溶液の体積は変化しますが、溶質の量は変化しないので、薄める前の溶質の物質量と薄めた後の溶質の物質量は変わらないからです。
溶質の物質量で方程式を立てる
それでは解いていきます。
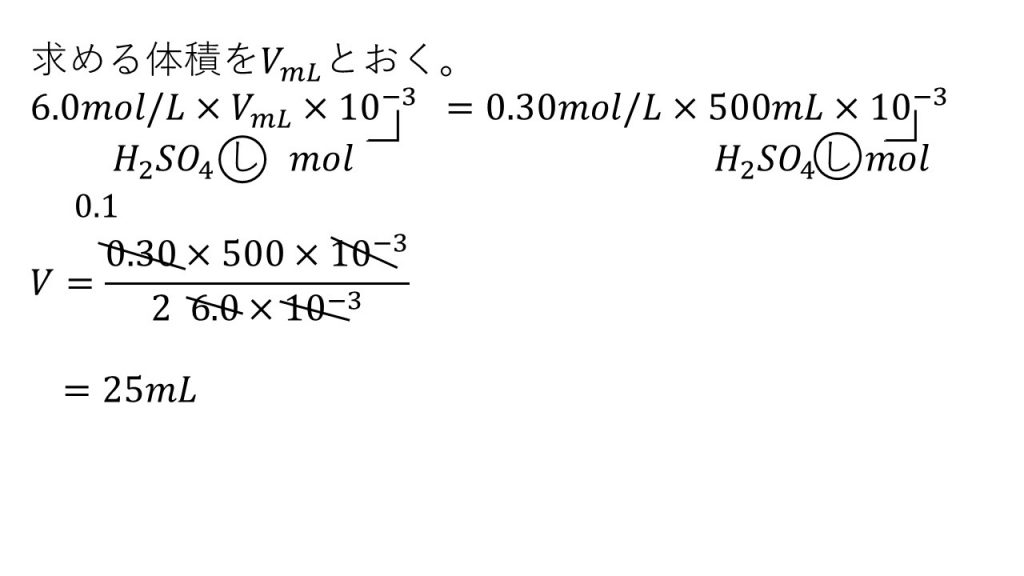
まずは求めるものを文字でおきます。
そして左辺は薄める前の溶質の濃度にします。モル濃度に溶液のリットルをかけることで溶質のモルとなります。
また右辺は薄めた後の溶質のモルになるようにします。薄めた後のモル濃度に薄めた後の溶液のリットルをかけることで溶質のモルとなります。
そして薄める前と薄めた後では溶質のモルに変化がないので方程式ができます。
工夫しながら方程式を解く
あとはこの方程式を解いていきます。
方程式を計算するときの基本は、求める文字だけを左辺に残し、それ以外をすべて右辺にもっていくことです。
そして、約分できるだけ約分していきます。あとは残ったもので計算すると答えは25mLとなります。
このように溶質の物質量で方程式を立てるという解き方はできるようになっておきましょう。
問題③:濃度変換(質量パーセント濃度をモル濃度に変換する)
それでは最後にこのような問題を解いてみます。
質量パーセント濃度98%で、密度が1.8g/cm3の濃硫酸のモル濃度を求めます。ただし、硫酸の分子量は98とします。
この問題は質量パーセント濃度をモル濃度に変えるので、濃度変換の問題と呼ばれています。このような濃度変換の問題ができるようになれば、濃度計算の基本は身についたといえます。
それでは解いていきましょう。
問題文の情報の確認
まずは問題文の情報を確認します。
今回は濃度と密度の情報がありますが、どちらも溶液の情報です。濃度の問題において、密度が与えられた場合は、基本的に溶液の密度であるということは知っておきましょう。
溶液の体積を1Lとする
まず濃度変換の問題は、濃硫酸つまり溶液の体積を1Lとするところから始めます。ちなみに1cm3を1mLと定義しているので1Lは1000cm3となります。
なぜこのように溶液の体積を決めるのでしょうか。
濃度を溶質に変換するためには溶液の情報が必要であり、さらに密度を扱うためには体積の情報が必要だからです。
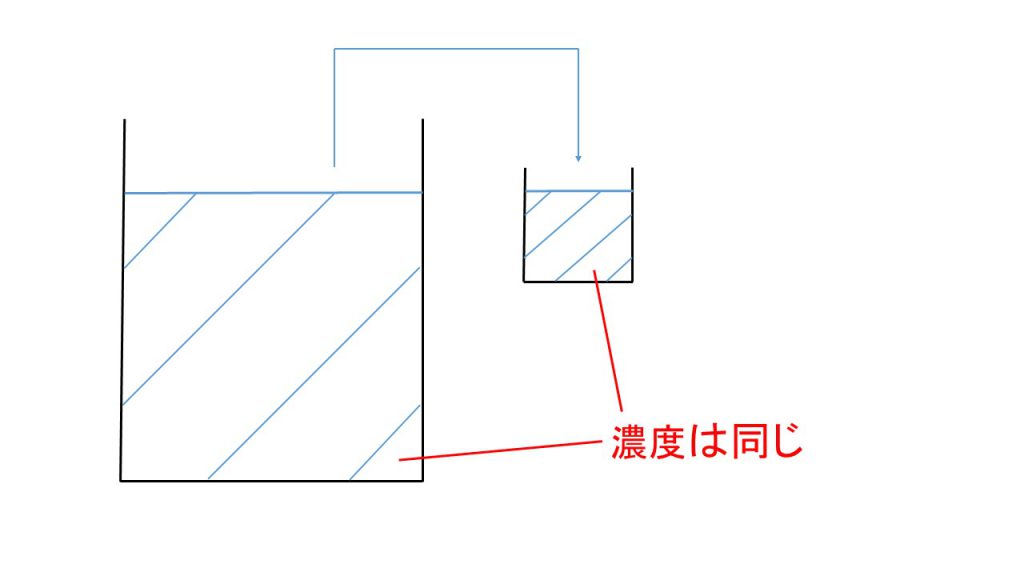
また勝手に体積を1Lとしてもいいのかというと今回は問題ありません。なぜなら濃度というものは溶液の体積によって変化することはないからです。
例えばある濃度の溶液があったとき、そこから一部を別の容器に移したとしても濃度は変わりません。であれば計算しやすい1Lと設定しても問題ないのです。
式を立てて計算する
それではこれで必要なものが揃ったので式を立てていきます。今回求めるモル濃度の式は以下のようになります。
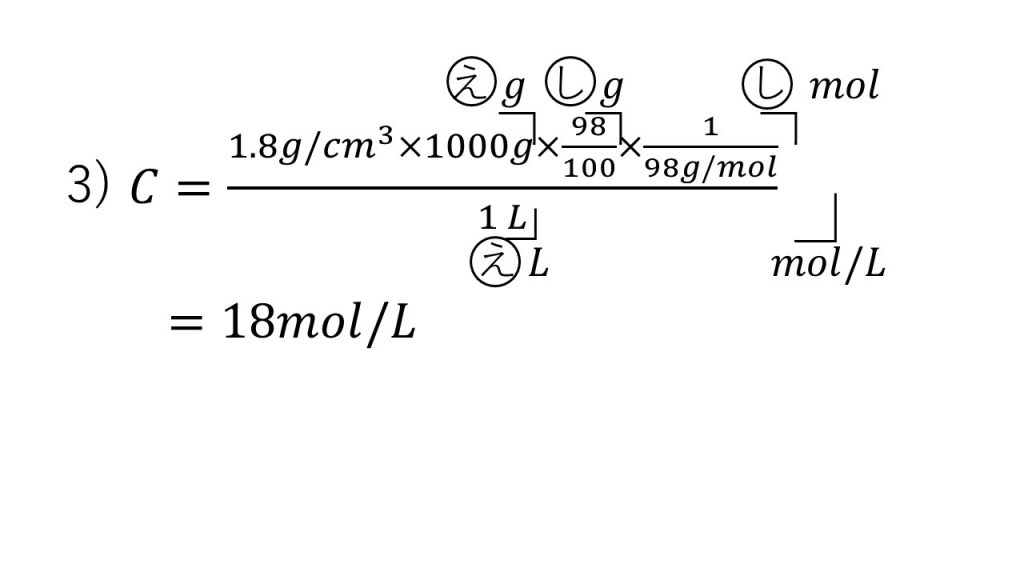
分母は溶液の体積なので1Lとなります。
そして分子ですが、分子は溶質のモルを求めます。
まず溶液の密度に溶液の体積をかけることで溶液の質量がでます。そして溶液の質量に質量パーセント濃度/100をかけることで、溶質の質量がでます。その溶質の質量をモル質量で割ることで溶質の物質量となるのです。
あとは計算ですが、約分をしていき、答えは18mol/Lとなります。
このように丁寧に単位と溶液なのか溶質なのかを追っていけば、濃度変換の問題も正確に解くことができます。
いかがだったでしょうか。
ⅰ)単位に気をつけながら分母と分子を順番にもとめる
ⅱ)溶質の物質量で方程式を立ててみる
ⅲ)溶質なのか溶媒なのか溶液なのかに気をつける、この3点を意識しながら濃度計算をしてみてください。
(3)解説授業の内容を復習しよう
(4)濃度計算の解説
①濃度計算の基本(質量パーセント濃度とモル濃度、濃度変換についても解説しています)
(5)参考
☆化学の解説動画・授業動画一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識テスト一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の解説・授業・知識・演習問題一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の語呂合わせ(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
「化学計算の王道」シリーズは『思考訓練の場としての体系化学』(GHS予備校)を参考にしています。
GHS予備校についてはこちら→https://ghs-yobikou.co.jp/
思考訓練シリーズの購入はこちら→https://ghs-yobikou.shop/
