(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
気体が外部にする仕事、気体が外部からされる仕事
気体が外部にする仕事について解説します。
気体が外部にする仕事の定義
気体が外部にする仕事は圧力×体積変化、
Wout=pΔV
で求めることができます。
気体が外部にする仕事と気体が外部からされる仕事の区別
気体の仕事を考える上で注意したいのは、「外部にする仕事」なのか、「外部からされる仕事」なのかを区別しないといけないということです。これらを区別しないと、正なのか負なのかややこしくなってしまい、ミスの原因となってしまいます。
そのため、「気体がする仕事」の場合はWout、「気体がされる仕事」の場合はWinと書くようにしましょう。
気体が膨張するとき、圧縮されるとき
気体がする仕事はpΔVで表されるので、気体が膨張つまりΔVが0より大きいときは、気体がする仕事は0より大きくなります。
ΔV>0 ⇒ Wout>0
そして気体が圧縮される場合、つまりΔVが0より小さくなるときは気体がする仕事は0より小さくなります。
ΔV<0 ⇒ Wout<0
さらに、気体がされる仕事で考えてみると、気体が膨張する場合は気体がされる仕事は0より小さくなり(Win<0)、圧縮される場合は気体がされる仕事は0より大きくなります(Win>0)。
このように、「する」のか「される」のかによって符号が変わるので注意しましょう。
「気体がする仕事」の意味
それでは、なぜ気体がする仕事は圧力×体積変化で求めることができるのか、考えてみましょう。
イメージで考えてみる
まずは、イメージで考えてみます。

圧力とは、気体がピストンを押す力と考えられるので、気体がピストンを押しながらΔVだけ膨張したと考えれば、P×ΔVが気体のした仕事となるのは分かると思います。
仕事の定義から考えてみる
また、仕事の定義から考えることもできます。力学で、仕事の定義は
W=F・s
と習いました。つまり仕事は「力(F)」に「力の向きに動いた距離(s)」をかけることで求めることができます。
ここで、それぞれの単位を確認してみます。仕事(W)の単位は[J]、力(F)の単位は[N]、距離(s)の単位は[m]です。つまり、
[J]=[N]×[m]
ということになります。
そして、pとΔVの単位を確認してみると、pは圧力なので[Pa]、ΔVは体積変化なので[m3]となりますが、圧力とは単位面積あたりにかかる力のことなので、[Pa]は[N/m2]と書くこともできます。
そして、[N/m2]に[m3]をかけることで、単位は[N・m]になります。つまりこれは[J]なので、p・ΔVは単位から考えてみると、仕事を表しているということが言えます。
p-Vグラフと仕事
また、気体が外部にする仕事は、p-Vグラフを使って求めることができます。つまり、p-VグラフとV軸で囲まれた面積が気体が外部にする仕事となるのです。
膨張(体積が増加)した場合のp-Vグラフ
例えば以下のようなp-Vグラフがあったとします。
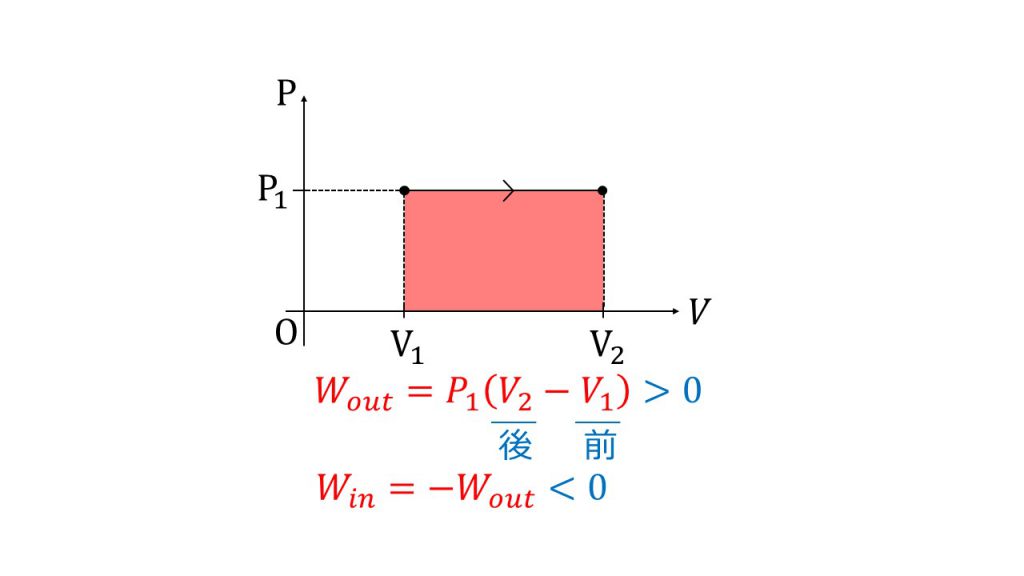
この変化は圧力が変わっていないので定圧変化となります。
この変化をした場合、気体が外部にした仕事は図の赤い部分の面積となります。つまり、この変化で気体が外部にした仕事は、「縦の長さP1×横の長さ(V2-V1)」となります。このように体積変化を求めるときは、必ず(変化後ー変化前)とするようにしましょう。そうすることで正負のミスをなくすことができます。
今回は正の方向にVが変化している、つまり気体が膨張しているので、気体がする仕事は正になります。(Wout=P1(V2-V1)>0)
ちなみに、気体がされる仕事は気体がする仕事と正負が逆なので、この場合は負となります。(Win=-Wout<0)
圧縮(体積が減少)した場合のp-Vグラフ
また、以下のグラフのように変化した場合は、気体がする仕事は、P1×(V1ーV2)となります。
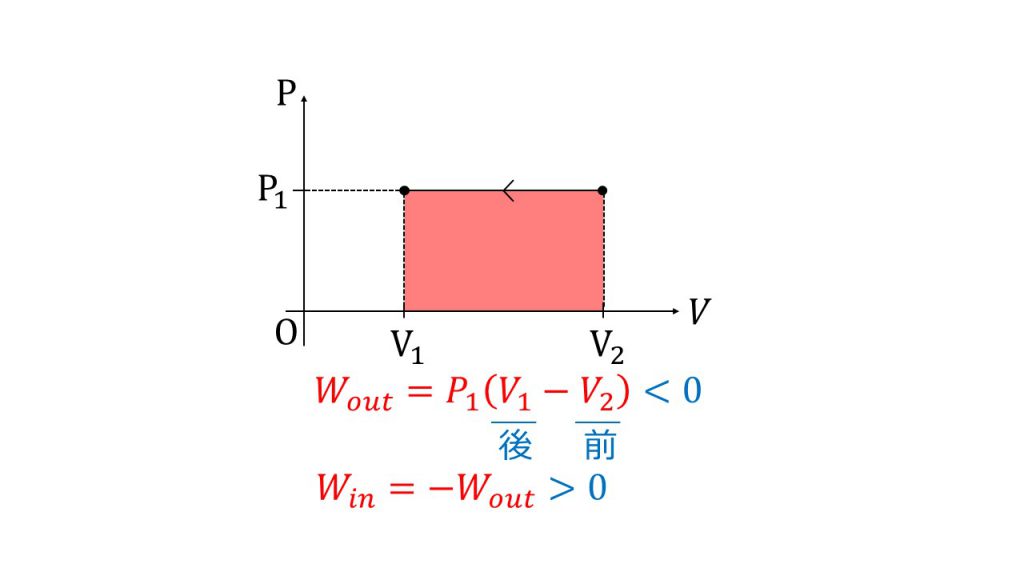
こちらも必ず(変化後ー変化前)とするようにしてください。体積が負の方向に変化しているので、気体が外部にする仕事は負となります。(Wout=P1(V1-V2)<0)
そして、気体が外部からされる仕事は正となります。(Win=-Wout>0)
熱機関のサイクル
また、p-Vグラフに関連して、熱機関のサイクルも確認してみます。
下図のように、ある状態から状態変化を繰り返し、元の状態に戻ってくることをサイクルといいます。そして、その過程で外部に仕事をする装置のことを熱機関といいます。
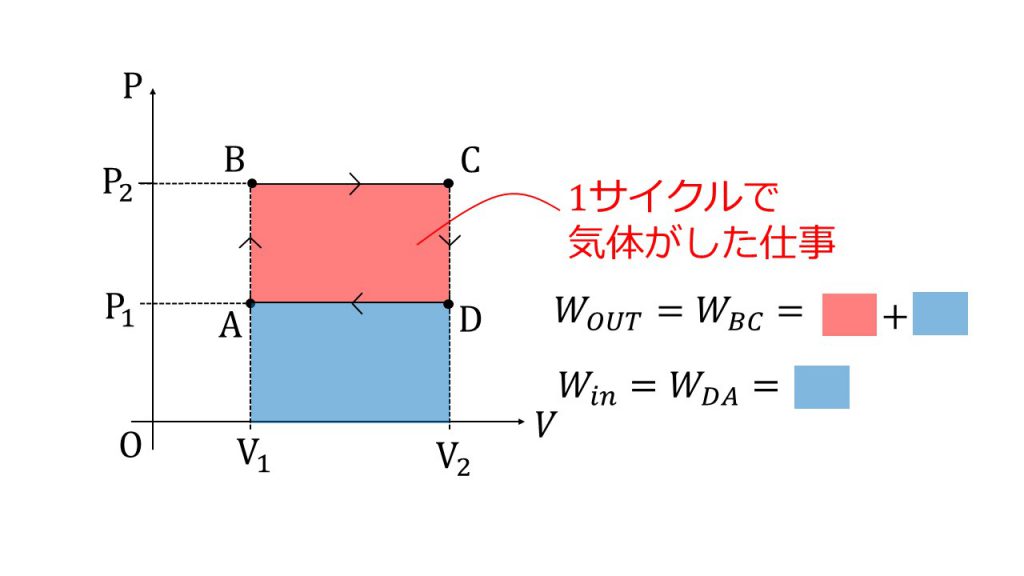
今回、この熱機関において、このp-Vグラフで囲まれた部分の面積が1サイクルで気体が外部にした仕事となります。
それはなぜかというと、AB, BC, CD, DAの各状態変化において、気体が外部に仕事をしているのはBC間だけであり、BC間における気体がする仕事は、赤色の面積+青色の面積となります。
そして、DA間では気体は圧縮されているので、気体は外部から仕事をされています。DA間における気体が外部からされた仕事は、青色の面積となります。
よって、この1サイクルでこの熱機関からとりだせる仕事は、(外部にした仕事ー外部からされた仕事)の赤色の部分の面積の分だけとなるのです。
状態変化と気体がする仕事
それでは次に、定積変化、定圧変化、等温変化、断熱変化の4つの状態変化において気体がする仕事がどのようになるか考えてみましょう。
定積変化と気体がする仕事
まず、定積変化ですが、体積は変化しないということなので、ΔV=0となり、p×0=0なので、気体は外部に仕事をすることはなく、外部から仕事をされることもありません。
定圧変化と気体がする仕事
次に、定圧変化ですが、定圧変化の場合はpが一定なので、気体が外部にする仕事はpΔVで圧力に体積変化をかけることで求めることができます。
等温変化・断熱変化と気体がする仕事
そして等温変化と断熱変化は、pとVの両方が変化します。そのため、Wout=pΔVの式で求める場合、積分を使わないといけません。
積分を使わずに気体がする仕事を求める場合は、熱力学の第1法則
ΔU=Qin+Win または Qin=ΔU+Wout
を使います。
等温変化の場合、温度が変化しないので、内部エネルギーも変化しません(ΔU=0)。そのため、気体がする仕事は吸収した熱量と等しくなり、気体がされる仕事は放出する熱量と等しくなります。(Wout=Qin、Win=Qout)
また、断熱変化の場合は、熱の出入りがない(Q=0)ので、気体がされる仕事は内部エネルギーの増加量と等しくなります。(W=ΔU)
断熱自由膨張
それでは最後に、断熱自由膨張という特殊な状態変化について解説します。
自由膨張とは、真空への膨張のことを言います。それを断熱容器の中で行えば、断熱自由膨張となります。
例えば下図のように2つの断熱容器があり、片方には気体が入っており、もう片方は真空でその2つの容器がコックでつながれているとします。この状態からコックを開くとこの容器の中の温度はどうなるでしょうか。
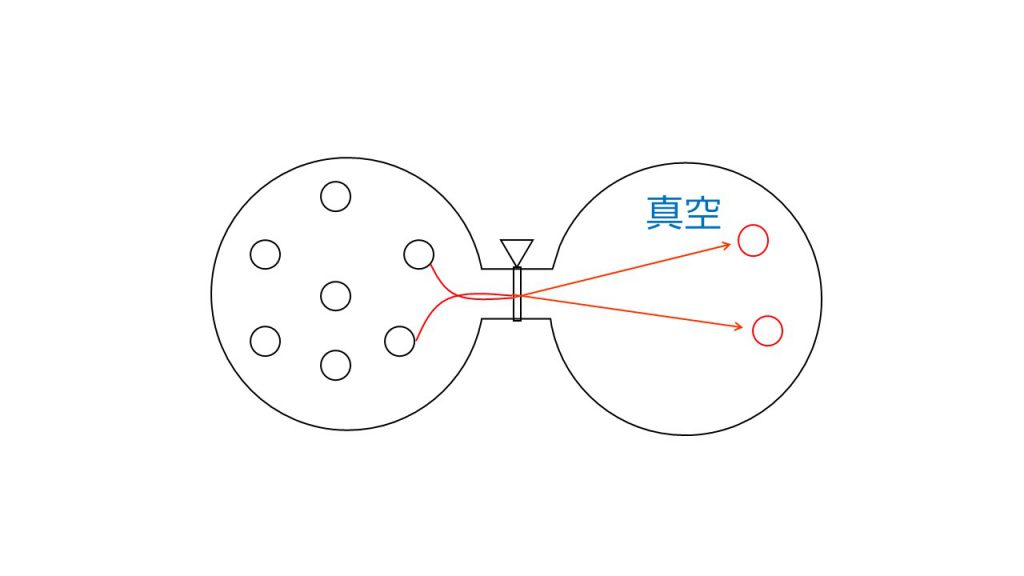
まず気体分子は真空だった容器にも拡散していくので、当然体積は増加します。しかし、自由膨張の場合、仕事はしたと見なされないので、気体がする仕事は0となります。なぜなら、真空への膨張なので、気体は自然に拡散していき、外部に対して仕事をしたとはいえないからです。
よって気体がする仕事は0(W=0)で、断熱なので熱の出入りもなく(Q=0)、熱力学の第1法則から考えて内部エネルギーの変化もありません(ΔU=0)。したがって、内部エネルギーが変化していないということは温度も変化しないということになります。
W=0
∴ΔU=0
したがってΔT=0
このように、断熱自由膨張の場合は、気体は膨張しているけれど温度は変化しないということになります。
(3)解説授業の内容を復習しよう
②気体の状態変化(熱力学)問題演習(2018年センター試験本試物理第4問B)
③気体の状態変化(熱力学)問題演習(2017年センター試験本試物理第3問B)
④気体の状態変化(熱力学)問題演習(2016年センター試験本試物理第5問)
(4)気体の状態変化(熱力学)の解説一覧
②気体の性質は気体分子で考えることで理解しやすくなります(気体の圧力、混合気体、ドルトンの分圧の法則、気体の運動エネルギー、気体の内部エネルギー、ボイルの法則、シャルルの法則、気液平衡、飽和蒸気圧)
③理想気体の状態方程式の使い方(理想気体とは何か、混合気体の考え方、計算の工夫の仕方についても解説しています)
④気体の内部エネルギーの表し方(内部エネルギーの増加量の3つの表し方、熱力学の第1法則、定積変化、定圧変化、等温変化、断熱変化、マイヤーの関係についても解説しています)
⑤気体が吸収した熱量の求め方(定積モル比熱、定圧モル比熱、熱力学の第1法則、定積変化、定圧変化、等温変化、断熱変化、熱効率)
⑥気体が外部にする仕事(pΔVになるわけ、p-Vグラフ、熱機関のサイクル、定積変化、定圧変化、等温変化、断熱変化、断熱自由膨張)
⑦定積変化・定圧変化・等温変化・断熱変化におけるp-VグラフとV-Tグラフ(ポアソンの法則についても解説しています)
(5)参考
☆物理の解説動画・授業動画一覧(力学・熱力学・波動・電磁気・原子)
☆物理に関する現象や技術(力学、熱力学、波動、電磁気、原子)
