条件付き確率の原理を解説します！（条件付き確率の公式、条件付き確率が意味すること、条件付き確率の求め方の流れについても解説します）

（１）解説授業動画

☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル

（２）解説授業の原稿

今回は条件付き確率について解説します。

条件付き確率を理解しているかどうかを試す問題

条件付き確率の原理を確認する前に、まずは以下の問題を考えてみましょう。

（問）硬貨2枚を同時に投げる。少なくとも1枚は表であるとき、2枚とも表である確率は？

この問題を正確に解くことができるでしょうか。この問題は条件付き確率を正しく理解していないと解くことができません。

1/2も1/4も誤り

1枚は表であることが確定しているので、残りの1枚が表か裏かのうち表になればいいので1/2

あるいは、1枚目が表で、2枚目も表になればいいので、

（〇, 〇）（〇, ×）（×, 〇）（×, ×）
※表を〇、裏を×とする。

硬貨の表裏の4パターンのうち2枚とも表になればいいので1/4

このように考えた方はいないでしょうか。

しかし、1/2も1/4も間違いで、1/3が正解になります。

なぜなら、この問題で求めないといけない確率は条件付き確率だからです。条件付き確率の原理を理解すれば、この問題で求める確率が1/3になる理由が分かると思います。

条件付き確率の原理

それでは、条件付き確率の原理を確認します。

条件付き確率の公式

条件付き確率の公式は以下のようになります。

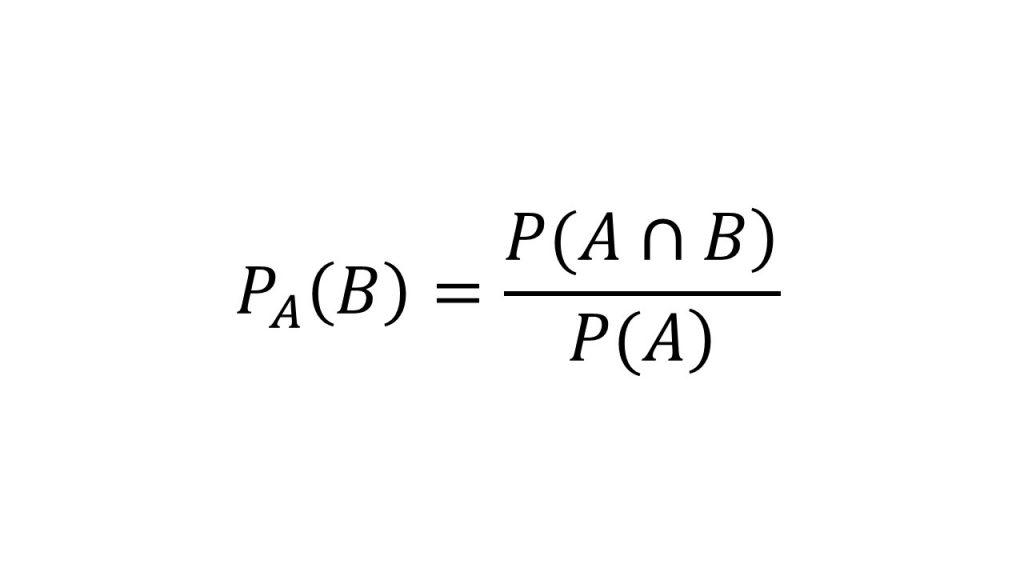
P_A(B)は「事象Aが起こったときに事象Bが起きる確率」を表しており、P(A)は「事象Aが起きる確率」を表しており、P(A∩B）は「A∩B(AかつB)が起きる確率」を表しています。

条件付き確率はこのように求めます。

条件付き確率の公式が表していること

では、この式は何を意味しているのでしょうか。

そもそもP(A)は、

事象Aの場合の数/U(全事象)の場合の数

で求めます。これが確率の基本的な求め方ですが、これが意味していることを図で表すと以下のようになります。

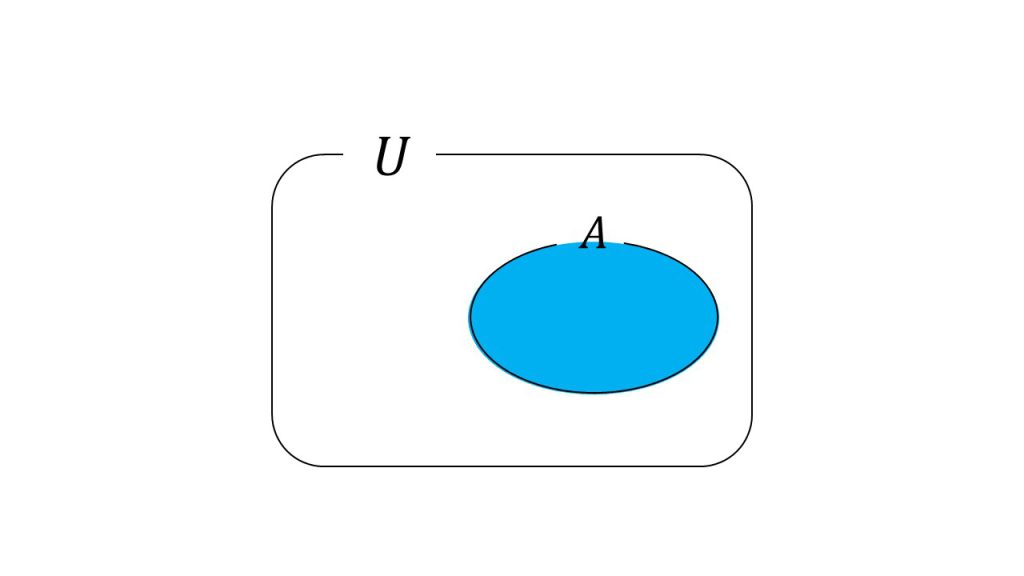
全事象の中で事象Aがどれだけの割合を占めているのかを表しています。

同様にP(A∩B)が意味していることは、

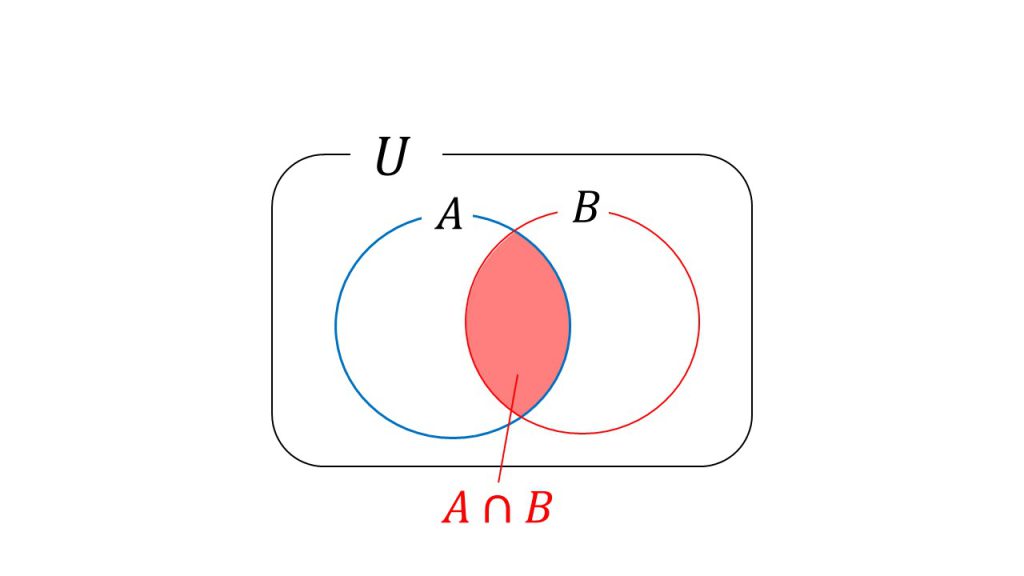
全事象の中でA∩Bがどれだけの割合を占めているのかを表しています。ちなみに、A∩BはAとBが重なった部分のことをいいます。

したがって、P_A(B)は、

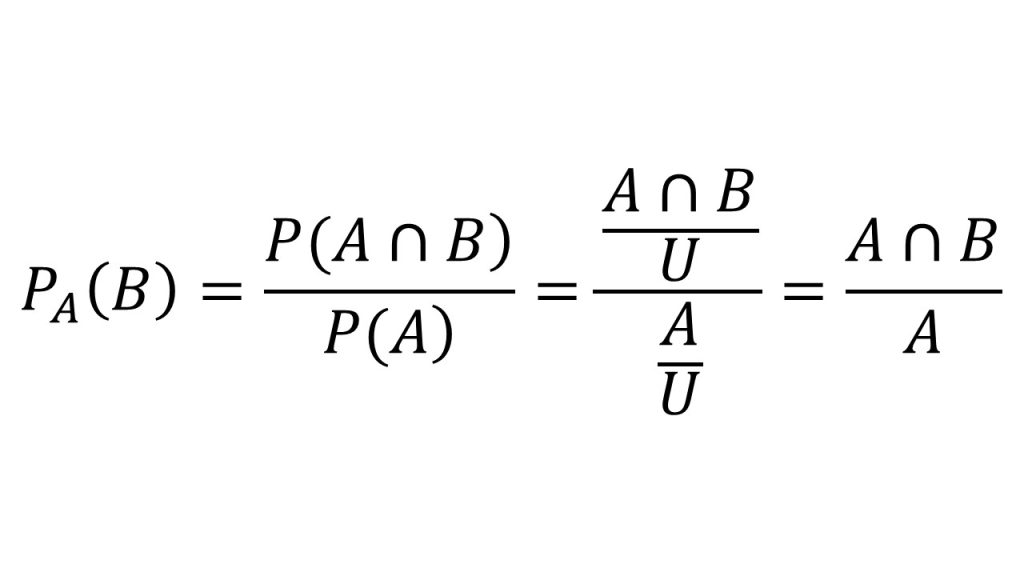
そして、このことが意味していることは、Aという事象の中でA∩Bという事象がどれだけの割合を占めているかということです。

つまり条件付き確率とは、もともとの全事象であるUではなく、Aを全事象として考えたときの、Bが起きる確率を求めているのです。

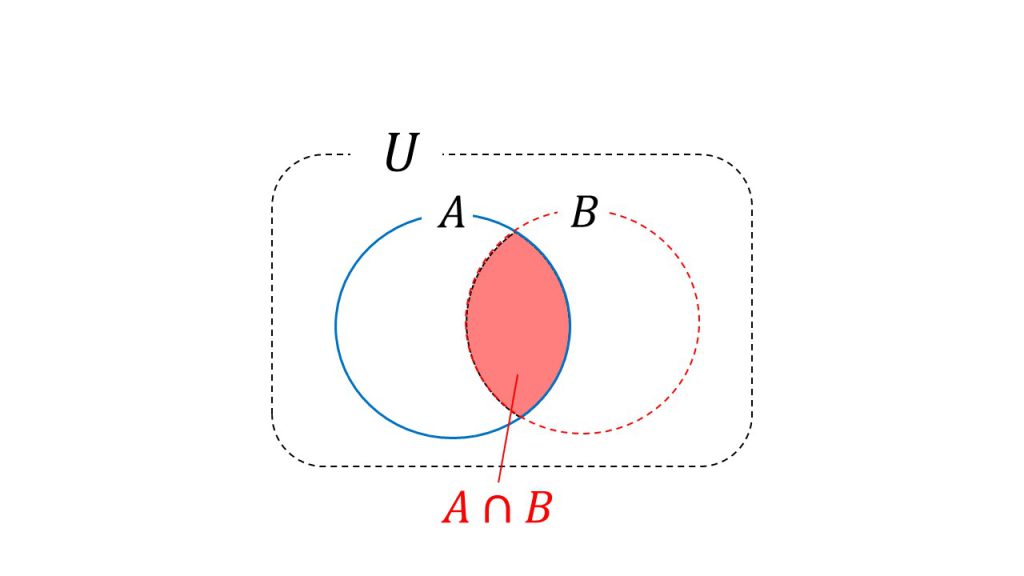
全事象をUとしたときは、Bはこれだけの部分を占めていましたが、Aという事象の中だけを考えてみると、Bが占める部分はA∩Bの部分だけになります。

よって、P_A(B)はAを分母にして、A∩Bを分子にして求めるのです。

このように、条件付き確率は全事象が変わったときに、確率がどのように変化するかを考えているのです。

これが条件付き確率の原理です。

再び問題を解く

それでは、最初の問題を条件付き確率の公式を使って解いてみます。

もう一度問題を確認します。

（問）硬貨2枚を同時に投げる。少なくとも1枚は表であるとき、2枚とも表である確率は？

まずポイントとなるのは、「～であるとき…である確率を求めよ」と問題に書いてあれば、条件付き確率を求める問題であると判断することです。

問題文に「条件付き確率を求めよ」とはっきり書いてあることは少なく、このように「～であるとき…である確率を求めよ」と書いてあることが多いので、自分で問題文を読んで条件付き確率の問題であると判断する必要があります。

それでは、答案を確認します。

（答）
「少なくとも1枚は表である」事象を事象A、「2枚とも表である」事象を事象Bとする。
表を〇、裏を×とすると、2枚の硬貨を投げると
（〇, 〇）（〇, ×）（×, 〇）（×, ×）
この4パターンになる。よって、
P(A)=3/4, P(A∩B)=1/4
したがって、
P_A(B)=P(A∩B)/P(A)=1/3

条件付き確率の問題であると判断したら、まず事象Aと事象Bを設定します。

基本的に「～であるとき…」の「～」を事象Aとして、「…」を事象Bとします。今回は「少なくとも1枚は表である」という事象をAとして、「2枚とも表である」という事象をBとします。

そして、事象Aと事象Bを設定したら、次はP(A)とP(A∩B)を求めます。

今回、Aの確率（「少なくとも1枚表になる」確率）は、2枚の硬貨の表裏の4パターン
（〇, 〇）（〇, ×）（×, 〇）（×, ×）
のうち、
（〇, 〇）（〇, ×）（×, 〇）
この3パターンなので、3/4となります。

また、A∩Bの確率（「少なくとも1枚表になり、かつ、2枚とも表になる」確率）は、
（〇, 〇）（〇, ×）（×, 〇）（×, ×）
のうち、
（〇, 〇）
このパターンだけなので、1/4となります。

そして、P(A)とP(A∩B)を求めたら、最後に公式通りに割り算をします。

したがって、

P_A(B)=P(A∩B)/P(A)=1/3

これが答えとなります。

この順番で解けば、条件付き確率は確実に求めることができます。

ちなみに、先ほどの条件付き確率の原理でこの問題を考えてみると、求めた条件付き確率は全事象をAとしている、つまり、

（〇, 〇）（〇, ×）（×, 〇）（×, ×）