数学的帰納法の分かりやすい答案の書き方（等式バージョン）

（１）解説授業動画

☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル

（２）解説授業の原稿

今回は等式を数学的帰納法を使って証明するときの分かりやすい答案の書き方を解説します。

数学的帰納法が分かりにくくなる2つの原因

数学的帰納法を使って証明をするときに、「とりあえず教科書のマネをしながら答案を書いてみたものの、いまいち何をやっているのか理解できていない」という方が多いのではないでしょうか。そこで今回は、教科書や多くの参考書に載っている数学的帰納法の答案の書き方にいくつか改良を加えて、分かりやすくした答案の書き方をご紹介します。

まず、そもそも数学的帰納法が分かりにくくなるには2つの原因があります。

①「今、何を証明しているのか」を見失ってしまう。
②「何を証明に用いてよいのか」つまり「何が仮定になっているのか」を見失ってしまう。

この2つのことを見失ってしまうので、数学的帰納法が分かりにくくなってしまうのです。

そのため、分かりやすい答案を書こうと思えば、この2つを明らかすればよいのです。

数学的帰納法の分かりやすい答案フォーマット（等式バージョン）

以下が、等式の数学的帰納法を使った証明の分かりやすく改良した答案のフォーマットです。順番に確認していきます。

不等式バージョンはこちら→数学的帰納法の分かりやすい答案の書き方（不等式バージョン）

「(ⅰ)n=1のとき」の書き方

数学的帰納法は、まずn=1のときに成り立つことを証明するところから始めます。

ここで、証明する等式にn=1を代入したものを書くようにすると分かりやすくなります。つまり、「【証明する等式にn=1を代入したもの】が成り立つことを証明する」と記述します。

このように「今、何を証明するのか」を明らかにすると、分かりやすくなります。

(ⅰ)で証明するのは【証明する等式にn=1を代入した等式】なので、【証明する等式にn=1を代入した等式】の左辺を計算し、【証明する等式にn=1を代入した等式】の右辺を計算すると、(左辺)=(右辺)となるので、【証明する等式にn=1を代入した等式】が成り立つということが示されました。

「(ⅱ)n=kのとき」の書き方

次に、【証明する等式にn=kを代入したもの】が成り立つと仮定します。

これは「成り立つと仮定したもの」なので、これから証明するものではありません。仮定は、証明するものではなく、証明で使うものであるということに注意しましょう。

「n=k+1のときの～」の書き方

そして、【証明する等式にn=k+1を代入したもの】を書きます。つまり、(ⅱ)で証明するものは【証明する等式にn=k+1を代入した等式】なので、それを明確に記述すると分かりやすくなります。

ここから証明するのは【証明する等式にn=k+1を代入した等式】なので、【証明する等式にn=k+1を代入した等式】の左辺を式変形していきます。その式変形の中で、仮定である【証明する等式にn=kを代入した等式】を使います。

そして、今証明している【証明する等式にn=k+1を代入した等式】の右辺と同じ形になるようにします。

すると、(左辺)=(右辺)となるので、この【証明する等式にn=k+1を代入した等式】が成り立つことが示されました。

結論の書き方

したがって、(ⅰ)と(ⅱ)より、数学的帰納法によって、全ての自然数nにおいて問題の等式が成り立つこが証明されます。

ポイントは、

①今から証明する等式を明らかにすること
②仮定は証明で使う式であることを意識すること
③等式の証明なので、(左辺)=～から始めて、(左辺)=(右辺)を導くということ

この3点に注意して、等式を数学的帰納法で証明しましょう。

不等式バージョンはこちら→数学的帰納法の分かりやすい答案の書き方（不等式バージョン）

数学的帰納法の分かりやすい答案フォーマット（不等式バージョン）を使ってみる

それでは、先ほどのフォーマットを使って、実際に証明をしてみます。

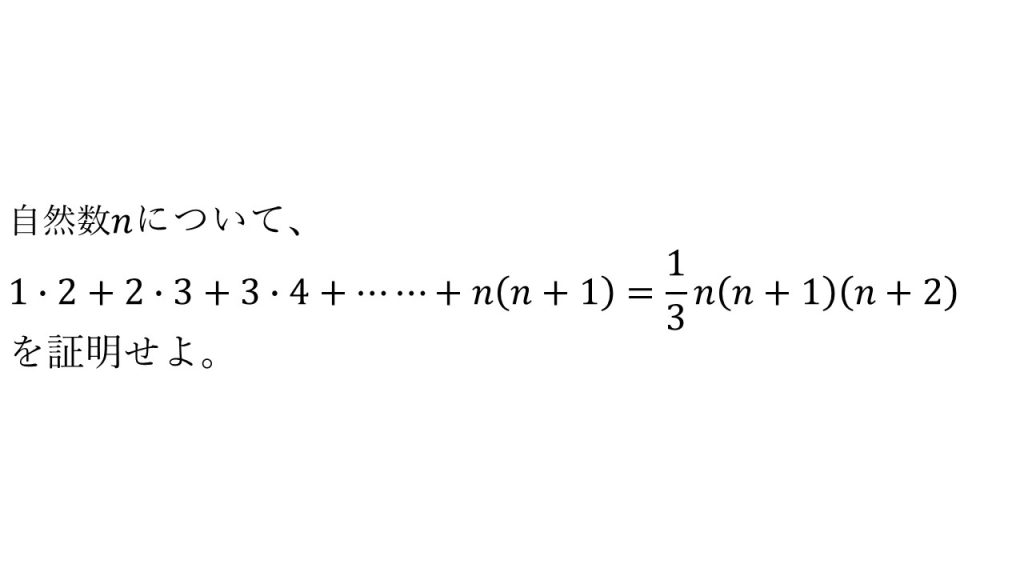
自然数に関する証明は数学的帰納法を使うことが多いです。

それでは、先ほどのフォーマットを使って、この等式を証明します。

n=1のときの証明

まずは、【証明したい等式のn=1を代入した等式】を書きます。つまり、「1・2=⅓・1・(1+1)(1+2)が成り立つことを証明する」と記述します。(ⅰ)では、【証明したい等式のn=1を代入した等式】を証明しているということを意識します。

この【証明したい等式のn=1を代入した等式】を証明するために、【証明したい等式のn=1を代入した等式】の左辺を計算し、【証明したい等式のn=1を代入した等式】の右辺も計算します。すると、左辺と右辺がともに2となるのでとなるので、この【証明したい等式のn=1を代入した等式】が成り立つことが示されます。

n=kのときの仮定

続いて、【証明したい等式にn=kを代入した等式】を書き、「【証明したい等式にn=kを代入した等式】が成り立つと仮定する」と記述します。

つまり、【証明したい等式にn=kを代入した等式】は仮定なので、後で証明で使う式であるということになります。

n=k+1のときの証明

次に、【証明したい等式にn=k+1を代入した等式】を書き、「【証明したい等式にn=k+1を代入した等式】が成り立つことを証明する」と記述します。つまり、これから証明するのは、この【証明したい等式にn=k+1を代入した等式】であるということになります。

よって、この【証明したい等式にn=k+1を代入した等式】を証明したいので、【証明したい等式にn=k+1を代入した等式】の左辺から式変形を始めます。

式変形のポイントとしては、仮定である【証明したい等式にn=kを代入した等式】と同じ形を作るということです。今回で言えば、1・2+2・3+3・4+……k(k+1)が仮定の等式の左辺と同じ形になります。したがって、仮定より、1・2+2・3+3・4+……k(k+1)の部分は⅓・k(k+1)(k+2)（仮定の右辺）とすることができ、因数分解します。

そして今回は、【証明したい等式にn=kを代入した等式】を証明しているので、【証明したい等式にn=kを代入した等式】の右辺と同じ形になるように式変形します。今回は、⅓をくくり出すと、【証明したい等式にn=kを代入した等式】の右辺と同じ形になります。

よって、(左辺)=(右辺)となったので、【証明したい等式にn=k+1を代入した等式】も成り立つことが示されました。

結論

したがって、(ⅰ)n=1のとき問題の等式が成り立ち、(ⅱ)n=kのとき【証明したい等式にn=kを代入した等式】が成り立つと仮定したら、n=k+1のときも問題の等式が成り立つことが示されたので、数学的帰納法により、すべての自然数nにおいて、問題の等式が成り立つことが証明されました。

いかがだったでしょうか。このように、数学的帰納法を使うときは、「今、何を証明しているのか」、そして、「何を証明で使ってよいのか」、この2つを明らかにすると分かりやすくなります。もちろん、この2点を意識できるようになれば、教科書や多くの参考書のように、「何を証明するか」をわざわざ記述しなくても構いません。しかし、慣れるまでは、これらを記述しておいた方がよいと思います。ぜひ試してみてください。