(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
指数法則
指数の計算をするときは指数法則を使いこなすというのがポイントとなります。
指数法則とは、
①ar・as=ar+s
②ar/as =ar-s
③(ar)s=ars
④(ab)r=ar・br
主にこの4つが指数法則となります。簡単に言うと、掛け算は足し算になり、割り算は引き算になり、累乗は掛け算になるというのが指数法則です。
指数法則を使った計算のコツ
また指数法則を使った計算のコツとして、累乗根は分数乗に直しましょう。
例えば、
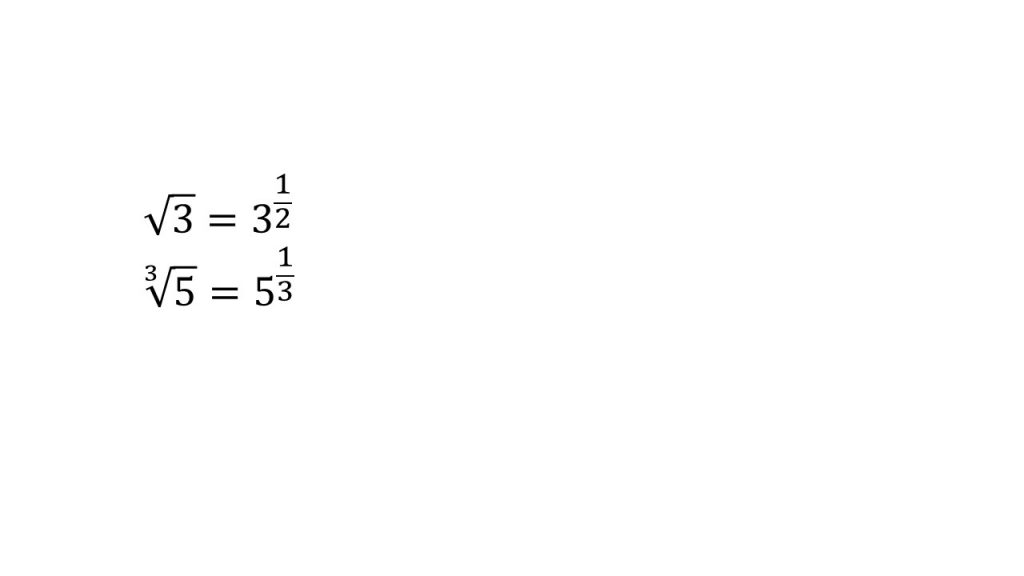
とします。こうすることで累乗根が指数となり、指数法則が使えるようになります。
また割り算や分数は-1乗しましょう。
例えば
a2÷b3=a2・b-3
a2/b3 =a2・b-3
としておけば、指数法則が使いやすくなります。
例題で指数法則を使いこなす
それでは実際にこれらを使って問題を解いてみましょう。
(例題)

(答)

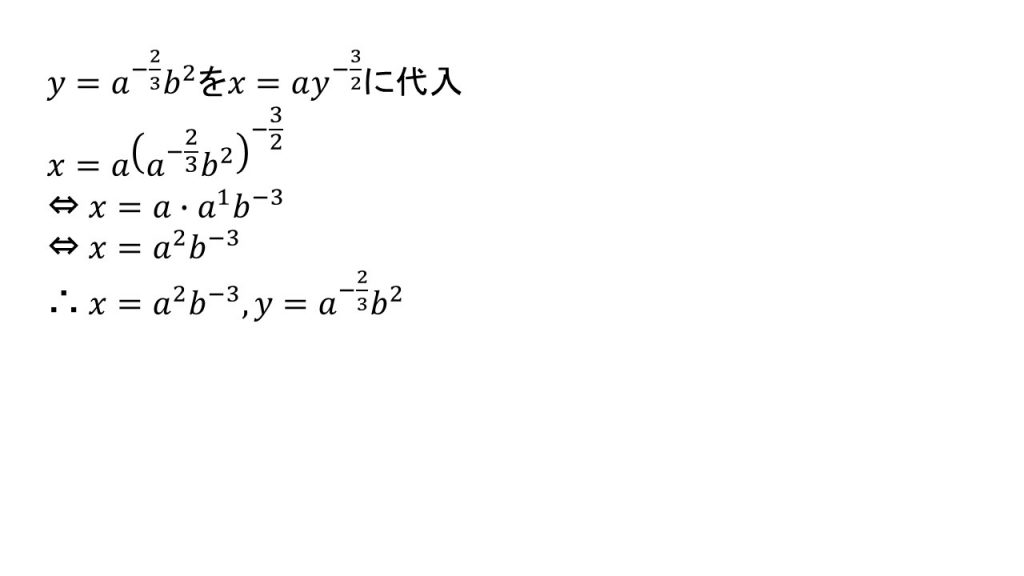
基本の方針としては、与えられた2つの式を連立させてxとyを求めるので、1つ目の式を式変形し、x=~の形にし、それを2つ目の式に代入してyを求め、その後xを求めるという流れになります。その計算を指数法則を使って正確に、かつ楽に計算してみましょう。
x=~の形にする
まずは、ルートを1/2乗にしましょう。すると
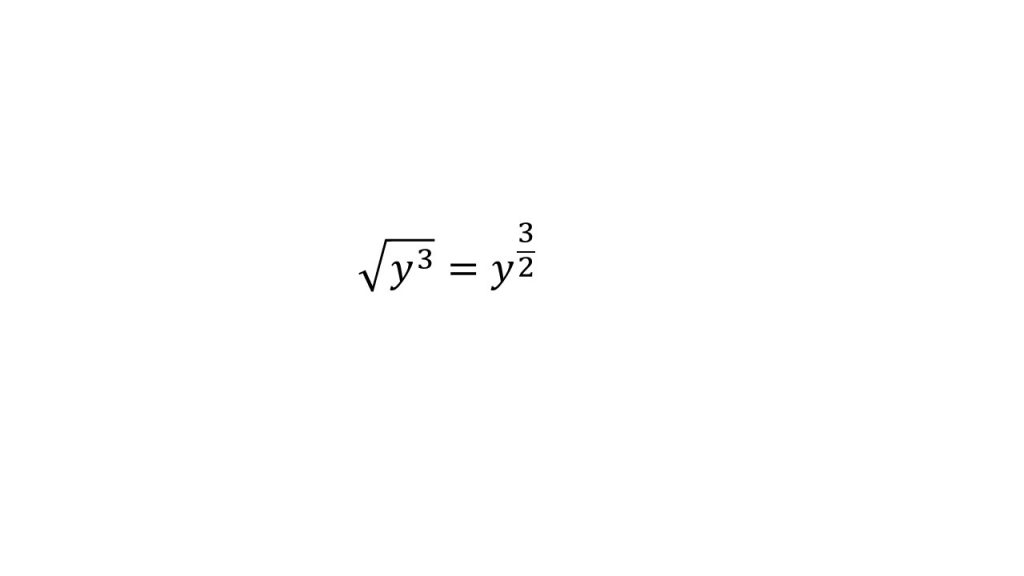
となります。
次に1つ目の式をx=~の形にします。その際、両辺をy3/2で割ります。それはつまり両辺をy-3/2でかけるということになります。
ここで、「割り算や分数は-1乗する」というポイントを使いました。よく3/2の逆数であるy2/3をかけてしまう人がいるのですが、これは間違いですので注意してください。
x=~の式を代入してyを求める
1つ目の式をx=~の形にできたので、次にそれを2つ目の式のxに代入していきます。
この式の3乗根も同様に1/3乗にします。そしてxに代入すると、以下のようになります。

ここでもしっかりこの指数法則を使って、かっこを外します。
あとはy=~の形にしたいので、この両辺を2乗します。

これでyを求めることができました。
y=~を代入してxを求める
次にx=~の式にy=~を代入すると
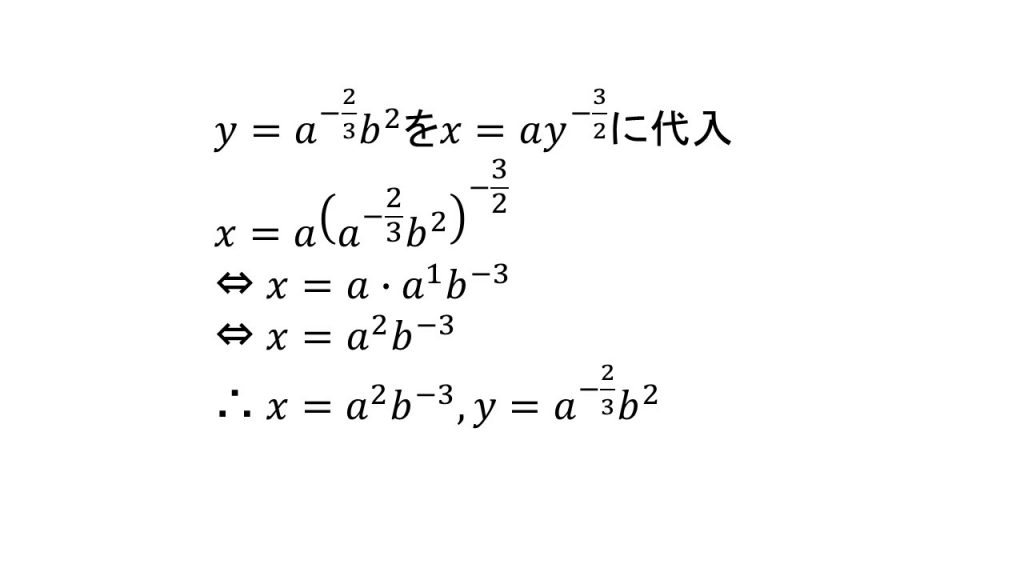
このようになり、指数法則を使ってかっこをはずし整理すると答えとなります。
このように累乗根などが含まれているときは、すべて指数にしてしまい指数法則を使いこなして計算する方が早く楽に計算できます。
(3)解説授業の内容を復習しよう
(4)指数(数学Ⅱ)の解説一覧
②指数法則を使いこなそう(累乗根は分数乗に、割り算や分数は-1乗にする)
