場合の数におけるPとCの違いを解説します！

（１）解説授業動画

☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル

（２）解説授業の原稿

場合の数におけるPとCの違いについて解説します。

_nP_rと_nC_rの定義

まずはそれぞれの定義を確認します。

_nP_r：異なるn個のうちから異なるr個取り出して並べる順列

_nC_r：異なるn個のうちから異なるr個を取り出す組み合わせ

つまり、PとCの違いは、並べるか並べないかにあります。n個のうちからr個取り出すだけならばnCr、n個のうちからr個を取り出してその後並べるならばnPrということになります。

例題でPとCの使い方を確認

具体的に例題で確認してみます。

30人のクラスから
(ⅰ)委員長1人、副委員長1人、書記1人を選ぶ選び方が何通りあるか。
(ⅱ)委員会に入るメンバーを3人選ぶ選び方は何通りあるか。
(ⅲ)委員長1人と副委員長2人を選ぶ選び方は何通りあるか。

(ⅰ)の場合、まず、30人の中から役職が与えられる人を3人選びます。そして、そのあと、どの役職に就くかを決めるので、選んで並べていることになり、この場合は₃₀P₃となります。

(ⅱ)は役職を決めないので、30人の中から3人を選ぶだけであり、₃₀C₃となります。

このように、選ぶだけなのか選んだ後に並べるのかでPとCを使い分けます。

(ⅲ)の場合は、まずは委員長になる人を1人選ぶので₃₀C₁となり、さらに残りの29人から副委員長になる人を2人選ぶので₂₉C₂をかけます。
→₃₀C₁×₂₉C₂

このように同時に選ぶ場合は掛け算をします。

PとCの計算方法

また、PとCの計算方法を確認します。

₃₀P₃の場合は、₃₀P₃=30・29・28 となります。
₃₀C₃は、₃₀C₃=30・29・28/3・2・1 となります。

実際に計算するときは、このように計算すればいいのですが、それぞれもともとは以下のような式であるということは知っておきましょう。

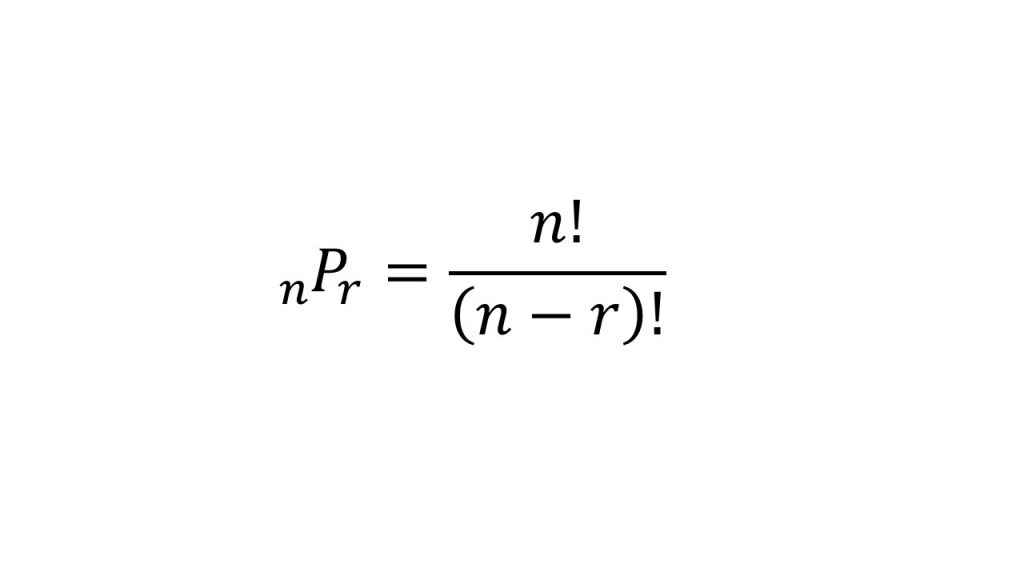
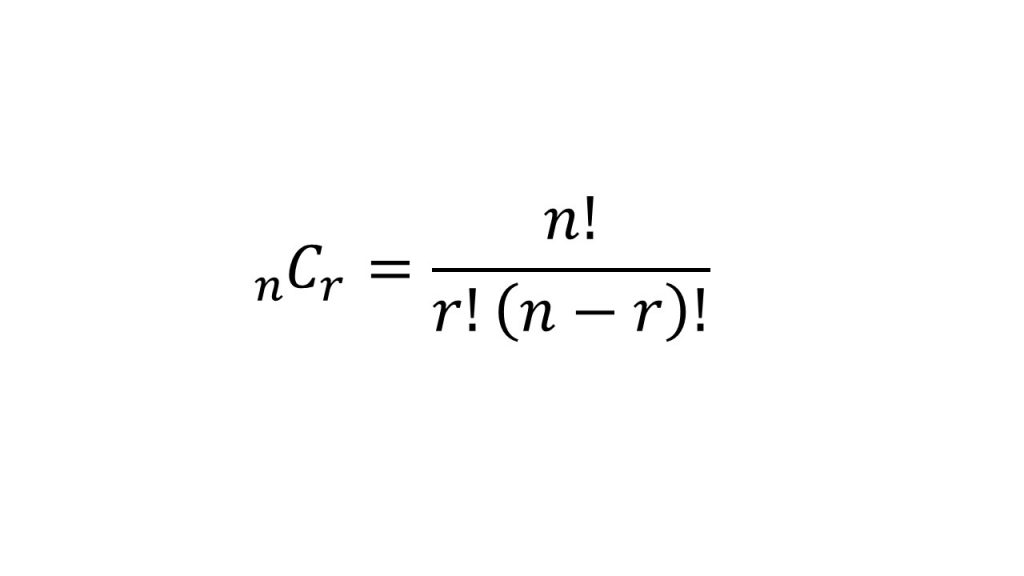
例えば₃₀P₃ならば、もともと

30!/(30－3)!=30!/27!

となり、約分されて30・29・28となっています。

また、₃₀C₃はもともと

30!/3!(30－3)!=30!/3!27!

であり、27!と30!を約分して30・29・28/3・2・1となっているということは知った上で計算するようにしてください。

（３）解説授業の内容を復習しよう

問題作成中

（４）順列と組み合わせ（数学A）の解説一覧

①順列と組み合わせ（数学A）の公式一覧

②同じものを含む順列の原理（なぜ同じものの階乗で割るのか、最短経路）

③正の約数の個数とその総和の求め方の原理

④場合の数におけるPとCの違いを解説します！

⑤円順列の原理（条件付きの円順列の問題の解説もしています）

⑥組分けの原理（なぜ組の数の階乗で割るのか）

⑦同じものを含むじゅず順列の問題の解法（じゅず順列の原理を理解しよう）

（５）確率（数学A）の解説一覧

①確率（数学A）公式一覧

②確率を理解する上で最も重要な問題（トランプの確率、数字と絵柄など2つの情報の扱い方）

③反復試行の確率の式の意味（なぜnCrをつけるのか、3つ以上の反復試行の確率の求め方についても解説しています）

④条件付き確率の原理を解説します！（条件付き確率の公式、条件付き確率が意味すること、条件付き確率の求め方の流れについても解説します）

（６）参考

☆順列と組み合わせ（数学A）の解説・授業・公式・演習問題一覧

☆確率（数学A）の解説・授業・公式・演習問題一覧

☆数学Aの解説動画・授業動画一覧

☆数学A公式一覧

☆数学Aの解説・授業・公式・演習問題一覧

☆数学の解説動画・授業動画一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学公式一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の解説・授業・公式・演習問題一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学典型パターン一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学の語呂合わせ

☆数学学習に必要な参考書・問題集