(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
図形の通過領域の問題の概要
図形の通過領域の問題では、図形を表す方程式にaなどの文字が含まれているため、そのaを変化させることで図形の形が変わっていきます。そして、そのように変化しながら動く図形が通る領域を図示する問題です。
まずは大雑把に解法の流れを確認します。
(例題)
直線ℓをy=ax+a2とする。aが全ての実数値をとって変化するとき、直線ℓの通り得る領域を図示せよ。
(答え)
y=ax+a2をaについて整理する。
a2+xa-y=0 ……(ア)
直線ℓが点(x,y)を通るとすると、(ア)を満たす実数aが存在しないといけない。つまりaについての二次方程式(ア)が実数解をもたないといけない。よって(ア)の判別式をDとすると
D≧0
x2+4y≧0
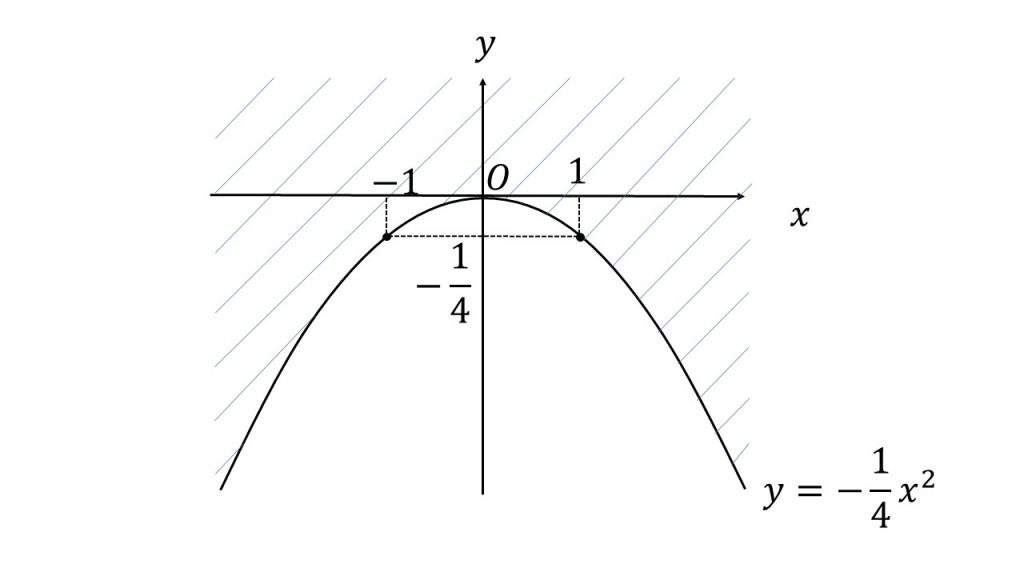
y≧-x2
したがって求める領域は図の斜線部分。ただし境界線を含む。
答案の解説
答案の流れ
最初に、この直線の方程式をaについて整理します。そして、このaについての二次方程式の判別式をDとすると、aは実数であるのでDが0以上となり、それを計算することでxとyの関係式ができるので、それを図示して答えとなります。
このように解法の手順自体はそこまで複雑ではないのですが、なぜこのようにすれば解けるのかを理解するのが難しいです。しかし、この解法を理解することが出来れば、軌跡や領域、あるいは関数といったものの理解がより深まります。
直線の方程式をaについて整理する理由
まずは最初に、なぜこの直線の方程式をaについて整理し直すという発想になるかですが、領域を図示する問題の基本として、特に断り書きがない場合は、xy平面に図示するということなので、問題文の条件からxとyの関係式を作らないといけません。
今回、問題文を一見しただけでは関係式が作れる条件が無いように見えますが、実は「aが全ての実数値をとる」ということが条件になっているのです。つまり「aは虚数ではなく実数である」という条件を使ってxとyの関係式を作らないといけないということになります。
それゆえ、aについての条件から式を作らないといけないので、aについて整理しようという発想が生まれるのです。
aについての二次方程式に含まれるxとyのとらえ方
次に、aについて整理した二次方程式、つまり、aについての二次方程式に含まれるxとyのとらえ方を考えてみます。
このxとyは、直線ℓが通る点の座標であると考えます。つまり求める領域内に存在するある点の座標を(x,y)とおいているということです。
求める領域内に存在しているので、この点は当然aがある実数値となるときの直線ℓの上にあるということになります。
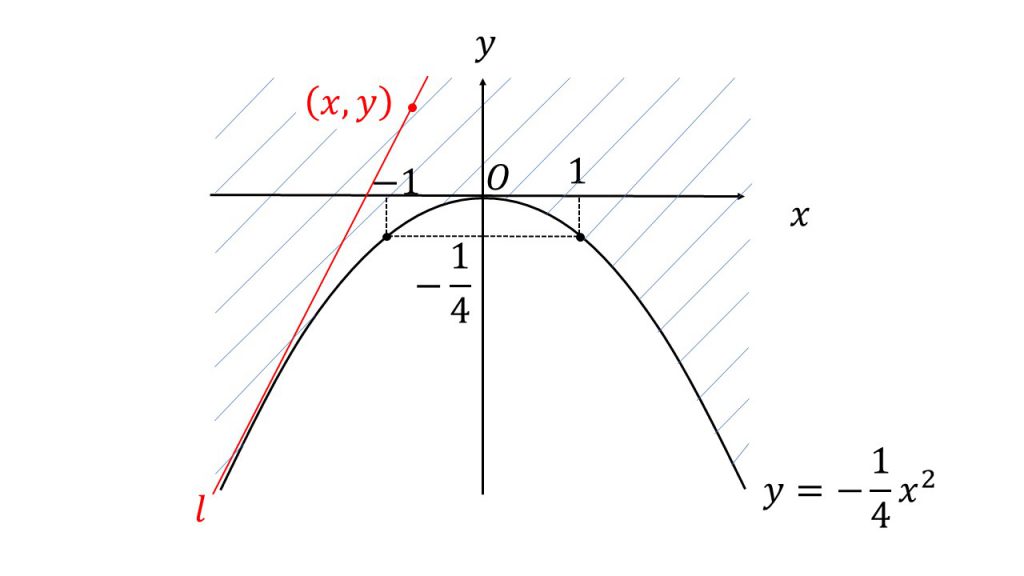
すなわち直線ℓは求める領域内に存在する点を通らないといけないので、この(x,y)を直線の方程式に代入しても成り立たないといけないし、それはつまり、この(x,y)をこの(ア)の方程式に代入しても成り立たないといけないということになります。
また、領域内に存在する点であれば、どの点の座標を代入しても(ア)の方程式が成り立つということは、領域外に存在する点の座標を代入したときはこの方程式が成り立たなくなるということにもなります。
方程式が成り立つということ→判別式を考える
方程式が成り立つということはその方程式が実数解をもたないといけないということであるので、求める領域内に存在する点の座標を(ア)のxとyに代入すれば、(ア)の方程式は実数解をもつことになり、逆に領域外の点の座標を(ア)のxとyに代入した場合はaは実数解とならない、つまり虚数解となります。
ゆえに、(ア)の判別式をDとしたときにDは0以上となり、(ア)はaについての二次方程式なのでその判別式はxとyの関係式となります。
このようにすることで、直線ℓが通る点の存在範囲が分かり、それはすなわち直線ℓの通り得る領域となるのです。
まとめ
もう一度以上の流れを整理すると、
①xy平面の領域の図示の問題なので、xとyの関係式を作らないといけないということ
②aが実数であるというのが今回の問題の条件なのでその条件を使ってxとyの関係を作らないといけないということ
③求める領域内の点を通るときℓの方程式に含まれるaは実数となり、逆に領域外の点を通るときの実数aは存在しないということ
これらを理解することが出来れば、この問題の解法の流れも理解できると思います。
この問題を理解することができれば、軌跡や領域をより深く理解することができるので、ぜひ今回の解説を理解できるまで繰り返し聞いたり、自分が納得するまで整理しながら考えてみてください。
(3)解説授業の内容を復習しよう
(4)軌跡と領域(数学Ⅱ)の解説一覧
①図形の通過領域の問題を理解して、軌跡や領域をより深く理解しよう
