和Snと漸化式

（１）例題

（２）例題の答案

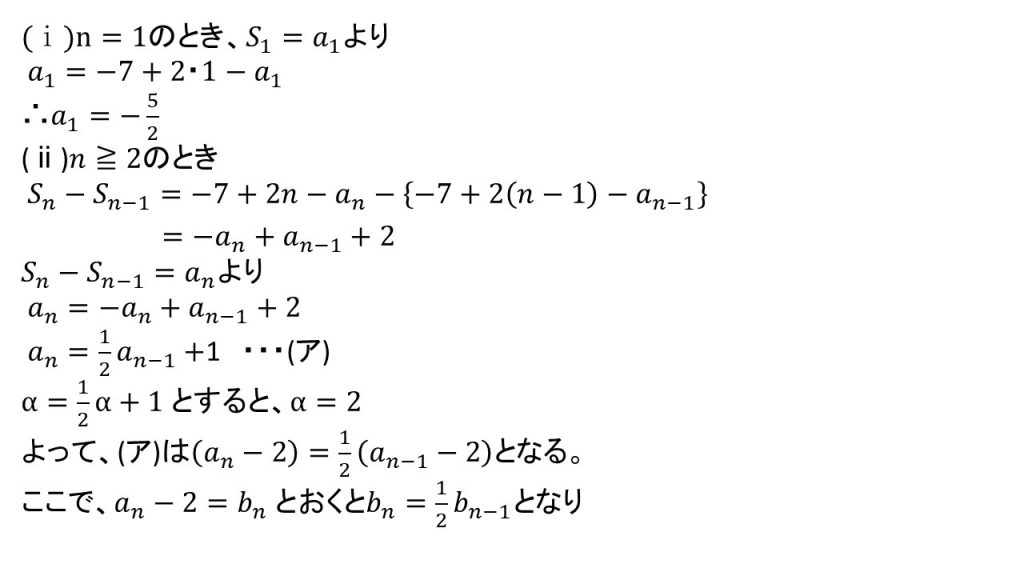
（３）解法のポイント

和の式が与えられている場合は、

①a₁＝S₁
②n≧2のとき、a_n=Sn－S_n-1

で、初項と一般項が求められます。数列の問題でn-1を扱うときは、n≧2の場合分けと、後でn=1の確認をすることを忘れないようにしてください。

また、a_nとa_n-1を含む漸化式は、nをn+1にして、a_n+1とa_nの漸化式とするとやりやすくなります。そのやり方はこちらを参照してください→a_nが分母と分子に含まれている漸化式

☆詳しい解説はこちら→漸化式をマスターしよう（２）基本パターン⑥（和Snが与えられているパターン、なぜn≧2としなければいけないのか）

（４）必要な知識

①和の式が与えられている漸化式

→和Snと漸化式解説動画

②等比数列の漸化式

→等比数列の漸化式解説動画

③特性方程式を利用して解く漸化式

→特性方程式を利用して解く漸化式解説動画

（５）理解すべきコア（解説動画）

①漸化式をマスターしよう（２）基本パターン⑥（和Snが与えられているパターン、なぜn≧2としなければいけないのか）

②漸化式をマスターしよう（２）基本パターン①（特性方程式を利用して解く漸化式、漸化式の解法の基本にして奥義）

③漸化式をマスターしよう（１）基本中の基本（等差数列の漸化式、等比数列の漸化式、そもそも漸化式とは何か）

（６）参考

☆漸化式をマスターしよう（２）基本8パターン

☆漸化式公式

☆漸化式（数学B）の勉強法

☆数列（数学B）の勉強法

☆数学的帰納法（数学B）の勉強法

☆数学Bの勉強法

☆数学Bの解説動画・授業動画一覧

☆数学B公式一覧

☆数学の解説動画・授業動画一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆数学公式一覧（Ⅰ・A・Ⅱ・B・Ⅲ）

☆計算のテクニック（数学）

☆絶対に知っておかないといけない数学の原則

☆数学に必要な思考法

☆数学学習に必要な参考書・問題集