(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
同じものを含む順列の公式
まずは同じものを含む順列の公式を確認します。

簡単に公式を説明すると、まず全てを区別して並べて、それを同じものの個数の階乗で割るというのが同じものを含む順列の求め方です。
例題で公式を確認する
例を使って確認してみます。
例えばaaabbcを1列に並べるときの並べ方を求めてみましょう。
まずはこのaaabbを全て区別して並べます。すると全部で6個の文字があるので6!とし、aaaの3つが同じものなので3!で割り、bbの2つも同じものなので2!で割ります。
6!÷3!÷2!=60通り
なぜ同じものの階乗で割るのか
ではなぜ同じものの数の階乗で割るのでしょうか。
例えばaaabbcを並べて、
ababca
このような並び方になったとします。もしこの3つのaをa1, a2, a3のように区別してみると、
a1ba2bca3
a1ba3bca2
a2ba1bca3
a2ba3bca1
a3ba1bca2
a3ba2bca1
このようにa1, a2, a3の3つの順列である3!=6パターンの並べ方が考えられます。しかし、この区別をなくした場合、これらのパターンはすべて同じ並べ方となるので3!で割らないといけないのです。
最短経路を求める問題
また、いわゆる最短経路を求める問題でもこの同じものを含む順列を使います。
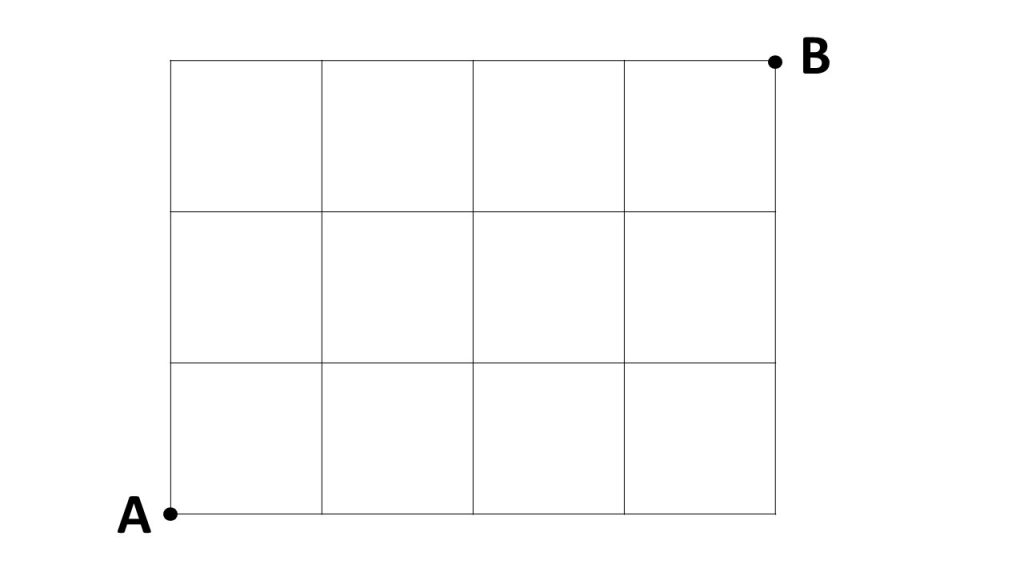
例えばこのような通路があり、AからBに最短で行く行き方は何通りあるかを求めてみましょう。
AからBに最短で行くには上に3回、右に4回移動します。そして、それぞれの交差点で上に行くか右に行くかを選択します。そのため、上に行くという選択を3回、右に行くという選択を4回することになるので、
↑ ↑ ↑ → → → →
の同じものを含む順列と考えて、7!を3!と4!で割って、答えは35通りとなります。
7!÷3!÷4!=35 通り
(3)解説授業の内容を復習しよう
(4)順列と組み合わせ(数学A)の解説一覧
②同じものを含む順列の原理(なぜ同じものの階乗で割るのか、最短経路)
⑦同じものを含むじゅず順列の問題の解法(じゅず順列の原理を理解しよう)
(5)確率(数学A)の解説一覧
②確率を理解する上で最も重要な問題(トランプの確率、数字と絵柄など2つの情報の扱い方)
③反復試行の確率の式の意味(なぜnCrをつけるのか、3つ以上の反復試行の確率の求め方についても解説しています)
④条件付き確率の原理を解説します!(条件付き確率の公式、条件付き確率が意味すること、条件付き確率の求め方の流れについても解説します)
(6)参考
☆順列と組み合わせ(数学A)の解説・授業・公式・演習問題一覧
