(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
三角方程式を解くときの流れ
三角関数を含む方程式のことを三角方程式といいます。この三角方程式をみたすθを求めることを、「三角方程式を解く」と言うのですが、三角方程式を解くときは、以下の5つの流れで解くようにしましょう。
①形を整える
②範囲を出す
③単位円をかく(単位円の中で範囲を確認する)
④線を引く
⑤単位円と線の交点からθの式を作る
この流れで取り組めば三角方程式を解くことができます。
例題①:sinの三角方程式
実際に例題で確かめてみましょう。
【問題】

【答案】

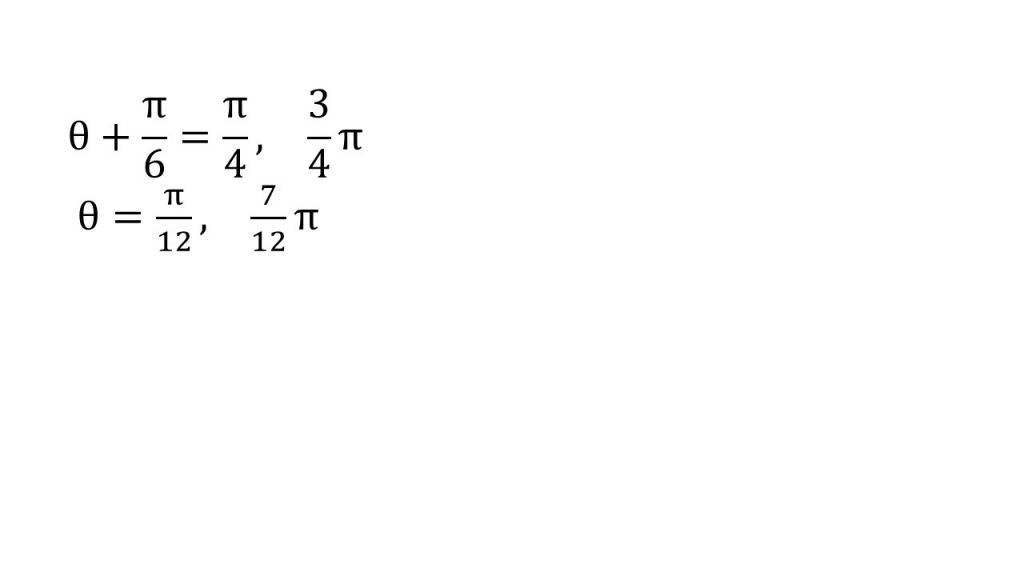
①まずは左辺をサインだけの形にするために、両辺を√2で割ります。このように左辺をサイン・コサイン・タンジェントだけの形にすることが1つ目のステップの「形を整える」ということです。
②次に範囲を出すのですが、今回求める範囲はθではなくθ+π/6の範囲を求めます。これが2つ目のステップです。
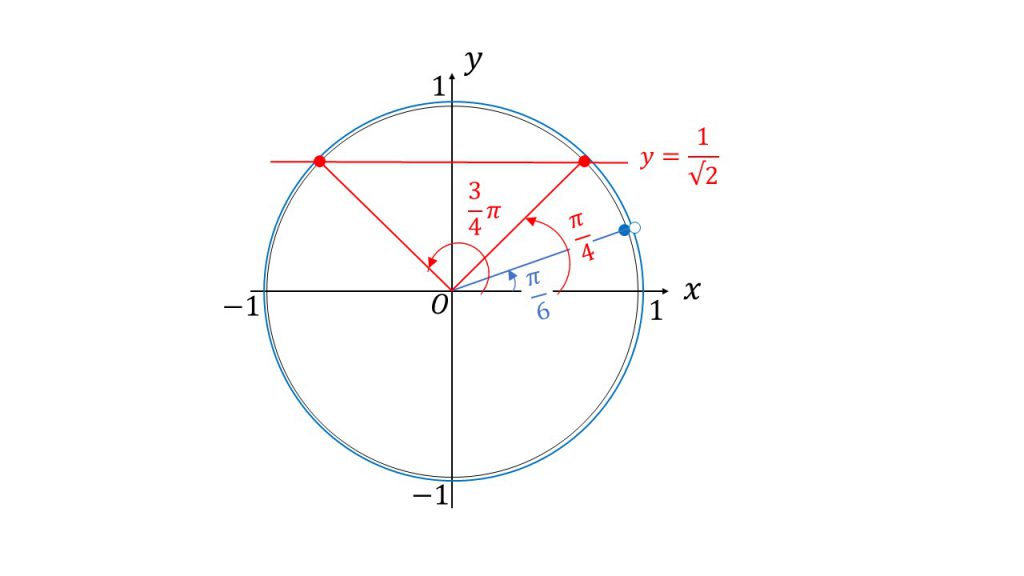
③そして単位円をかいて、その単位円の中でθ+π/6の範囲を確認します。単位円をかいて、単位円の中で今回の範囲を確認したら3つ目のステップとなります。
④次に線を引くのですが、今回はサインなのでy=の線をひきます。つまりx軸に平行なy=1/√2 の線をひきます。これが4つ目のステップです。
⑤最後に単位円と今引いた線との交点を確認してみると、角度がπ/4と3π/4のところに交点ができるので、θ+π/6=π/4, 3π/4という方程式ができます。これが5つ目のステップです。そしてこの方程式を解くことでθを求めることができます。
この5つのステップで三角方程式が解けることが確認できました。
例題②:cosの三角不等式
三角関数を含む不等式である三角不等式でも同様の流れで解けることを確認します。
【問題】

【答案】

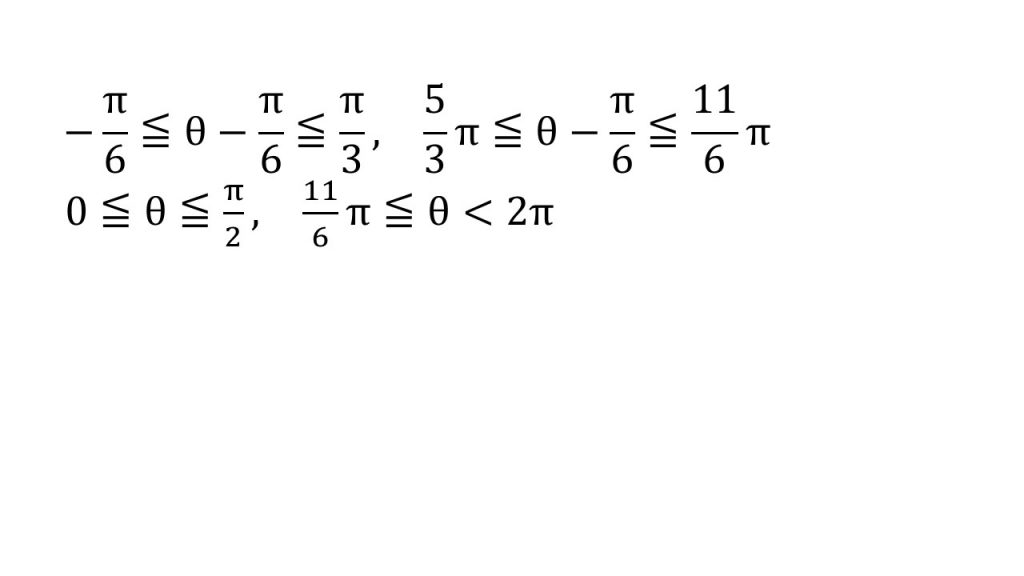
①まずは左辺をコサインだけにして1つ目のステップである形を整えます。
②そして、θ-π/6の範囲を求めます。これが2つ目のステップです。
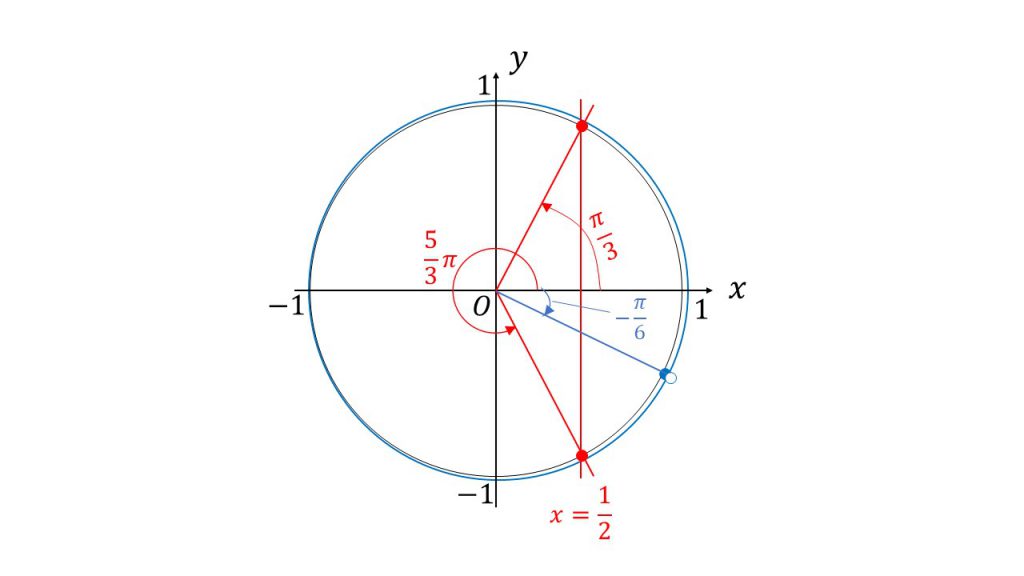
③続いて単位円をかいて単位円の中でこの範囲を確認します。これが3つ目のステップです。
④次に線を引くのですが、今回はコサインなのでx=の線を引きます。つまりx=1/2の線をひきます。これが4つ目のステップです。
⑤最後のステップとして単位円と線の交点を確認します。すると今回はπ/3の位置と5π/3の位置に交点ができます。ただし今回は不等式であるため、1/2以上つまりx=1/2よりも右側の部分が答えなので、θ-π/6の範囲の始まりに注意して、該当する範囲は-π/6≦θ-π/6≦π/3と5π/3≦θ-π/6<11π/6が今回の求める範囲となり、5つ目のステップとして不等式が2つできます。あとはこの2つの不等式を整理して答えが出ます。
このように不等式でもこの5つの流れで解くことができます。
例題③:tanの三角方程式
それでは最後にタンジェントの三角方程式でも確認してみます。
【問題】

【答案】

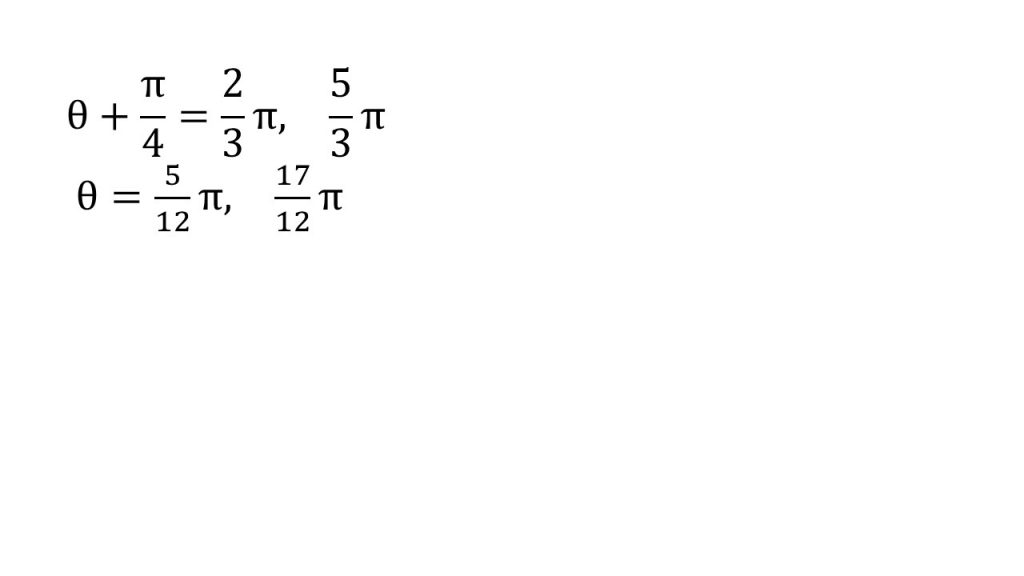
①②③まずは左辺をタンジェントだけの形にして形を整え、次にθ+π/4の範囲を求めます。そして、この範囲を単位円の中で確認します。
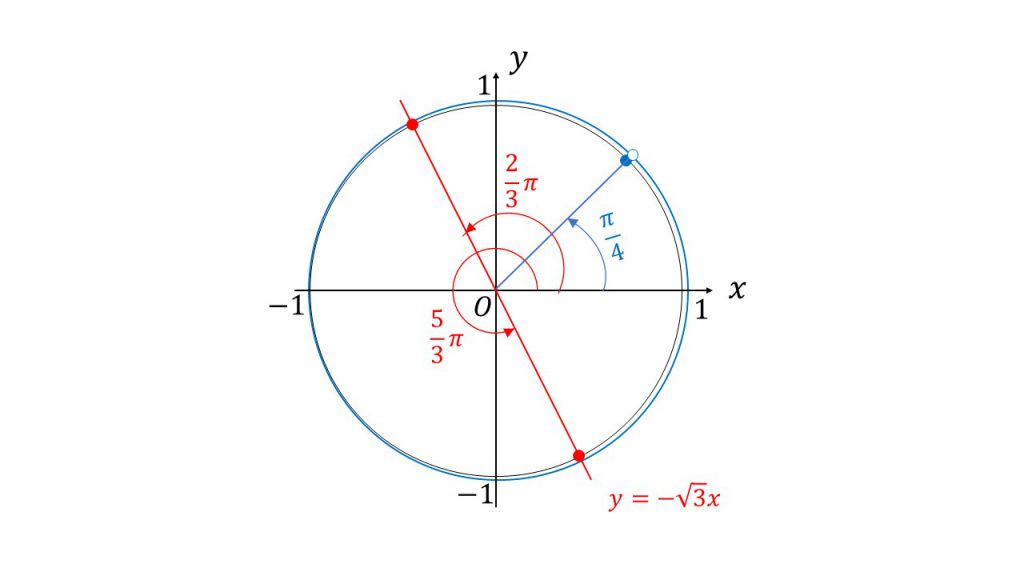
④次のステップとして線を引くのですが、タンジェントの場合は原点を通る直線つまりy=axの形の直線を引きます。今回で言えば、y=-√3xの直線を引きます。タンジェントの値というものは直線の傾きを示しているということは知っておきましょう。
⑤これで4つ目のステップとなり、次に単位円と直線の交点を確認します。すると単位円と直線の交点は2π/3と5π/3のところにできるので、θ+π/4=2π/3, 5π/3となり、これでθを含む方程式ができます。あとはθについて解いて答えとなります。
(3)解説授業の内容を復習しよう
(4)三角関数(数学Ⅱ)の解説一覧
②三角関数の性質は単位円で理解しましょう(θ+2nπ、−θ、π±θ、π/2±θ、単位円上の点の座標が(cosθ, sinθ)になる理由、tanθ=sinθ/cosθとなる理由についても解説しています)
③三角方程式・三角不等式の解法5ステップを解説します!(サイン、コサイン、タンジェントそれぞれで解説しています)
