そもそも判別式とは何か（二次関数の問題で判別式を使うときの注意点、二次関数と判別式の関係についても解説しています）

（１）解説授業動画

☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル

（２）解説授業の原稿

そもそも判別式とは何か

そもそも判別式は、解の公式から来ています。

ax²+bx+c=0という2次方程式があった場合、その解は

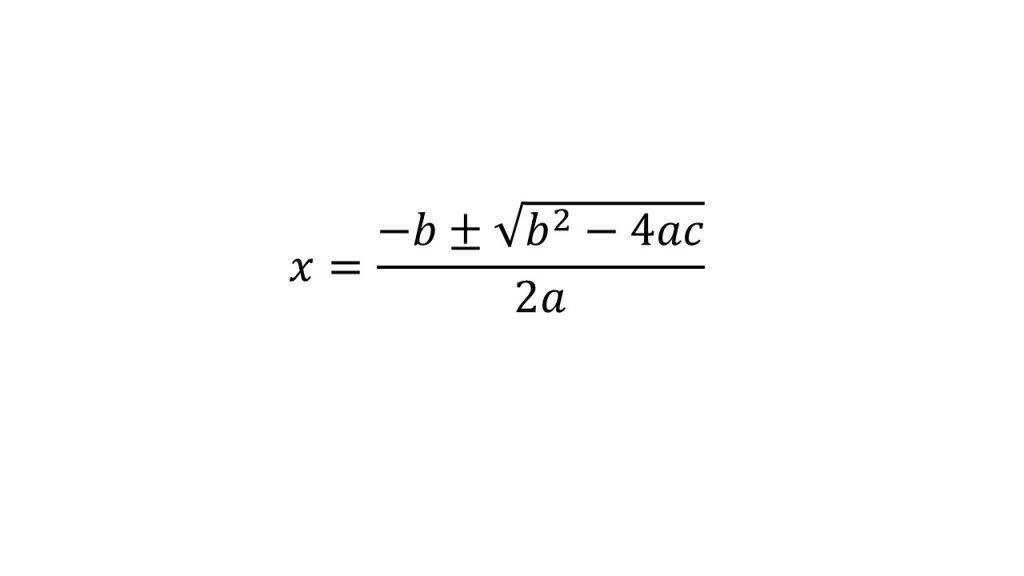
このようになります。

これを解の公式というのですが、この解の公式のルートの中の部分を判別式と呼んでいるのです。

判別式と二次方程式の解の個数

したがって、b²−4acつまり判別式が正のとき、この方程式の解はルートの前がプラスのときとマイナスのときで異なる実数解が2つとなります。

また、b²−4acつまり判別式が0のときは、この方程式の解はルートの中の部分が0になるので実数解が1つとなり、さらにその解はx=−b/2aとなります。

そして、b²−4acつまり判別式が0より小さいとき、この方程式の解はルートの中がマイナスになってしまうので、実数解は存在しません。

ルートの中が負になった場合は虚数となるので虚数解は存在します。こちらもルートの前がプラスのときとマイナスのときで異なる虚数解が2つとなります。

判別式を二次関数の問題で使うときの注意点

判別式は2次関数の問題でも使われます。

ただし、判別式を2次関数の問題で使うときは1つ注意点があります。

先ほど確認した通り、判別式は2次方程式の解の公式からきています。そのため、必ず「ax²+bx+c=0の判別式をDとすると」といったような記述を書くようにしてください。

判別式は2次方程式に対して使う言葉なので、こういった記述がないと判別式とは何かについて正しく理解していないとみなされてしまいます。

判別式と二次関数の関係

では2次方程式の判別式と2次関数がどのような関係になっているかを確認してみます。

判別式が0より大きいとき

まずax²+bx+c=0の判別式が0より大きいときは、2次関数y=ax²+bx+cのグラフとx軸の交点が2つになります。

それはなぜかというと、x軸を式で表してみるとy=0となり、y=ax²+bx+cという式とy=0という式を連立させてみるとax²+bx+c=0となります。

そして判別式が0より大きいということは、この2次方程式を満たす解つまりxが2つ存在するということであり、それはつまり、y=0とy=ax²+bx+cを同時に満たすxが2つあるということになります。

ということは、y=0のグラフとy=ax²+bx+cのグラフの交点のx座標が2つあるということになるので、2次方程式ax²+bx+c=0の判別式が0より大きいときは、2次関数y=ax²+bx+cとx軸の交点が2つ存在するということになります。

判別式が0になるとき

続いて同様に、2次方程式ax²+bx+c=0の判別式が0となるときに、2次関数y=ax2+bx+cのグラフとx軸の交点が1つになる、つまり接するのは、y=ax²+bx+cとx軸つまりy=0を同時に満たすxが1つであるので、y=ax²+bx+cのグラフとy=0のグラフの交点のx座標が1つとなるからです。