(1)複素数平面
①基本公式
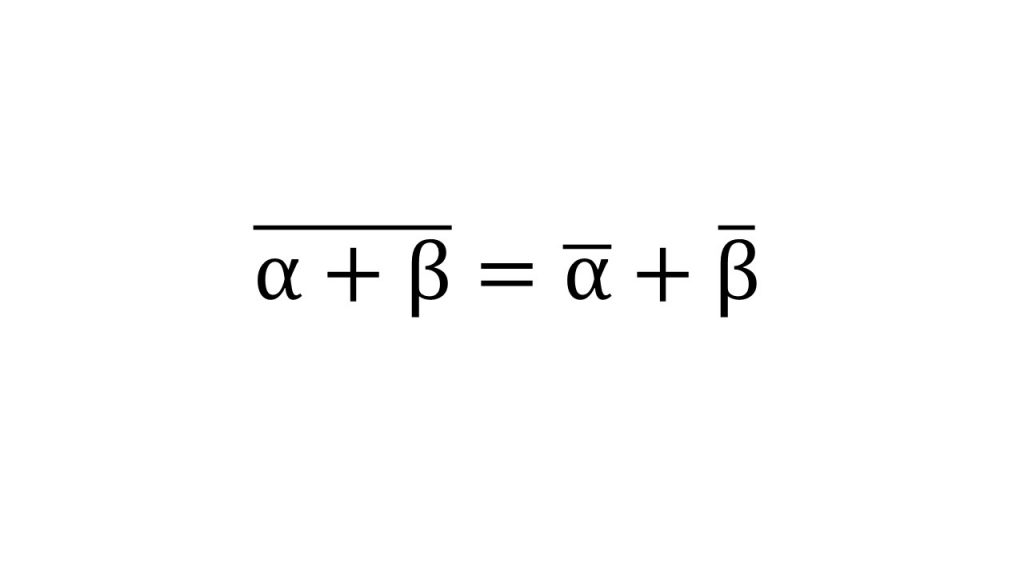
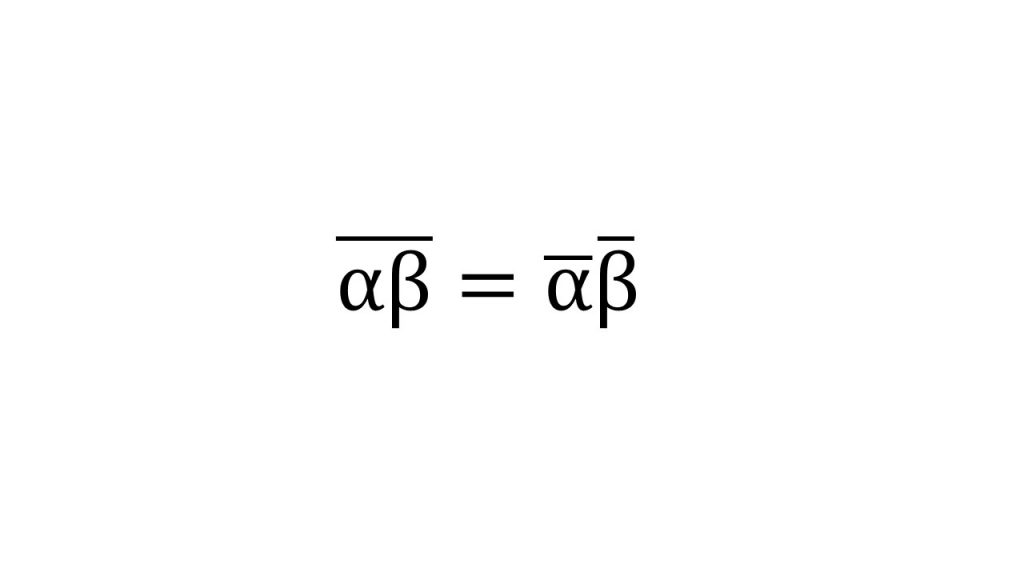
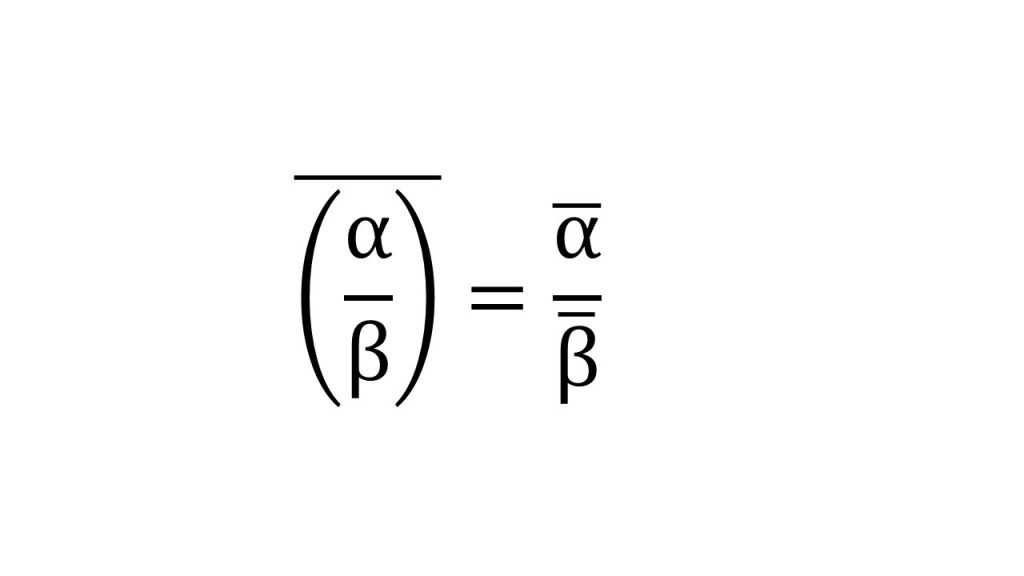
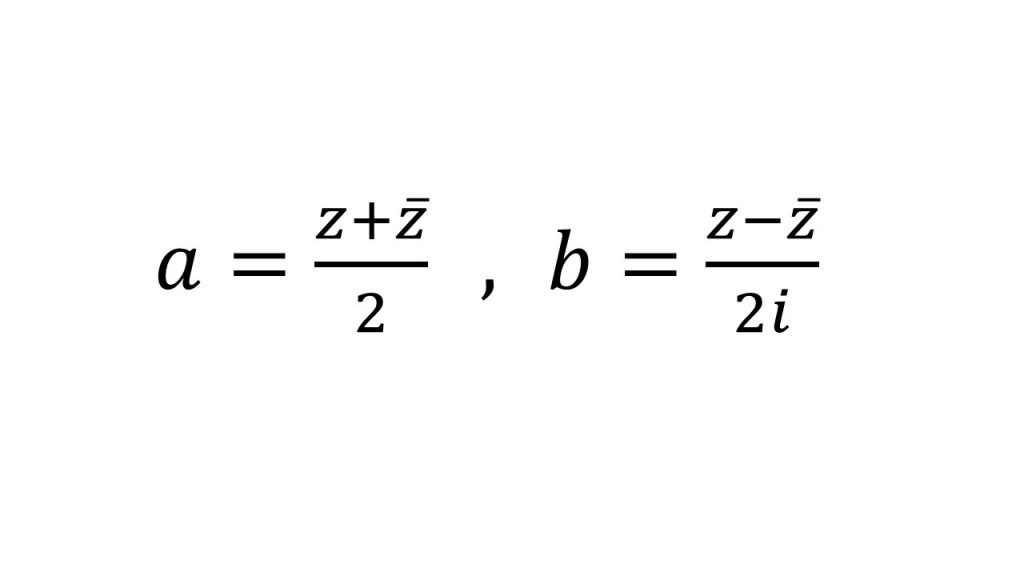

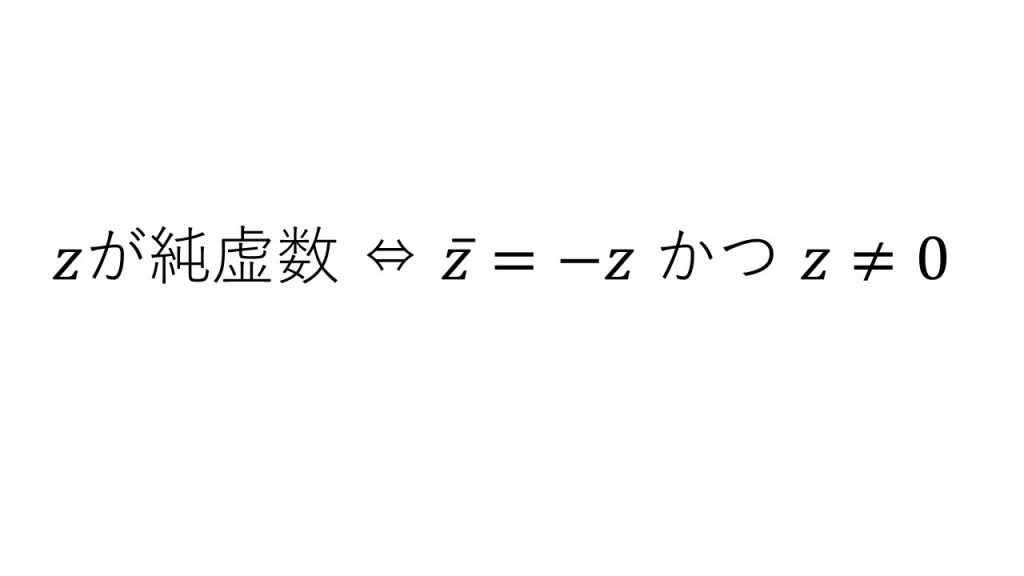
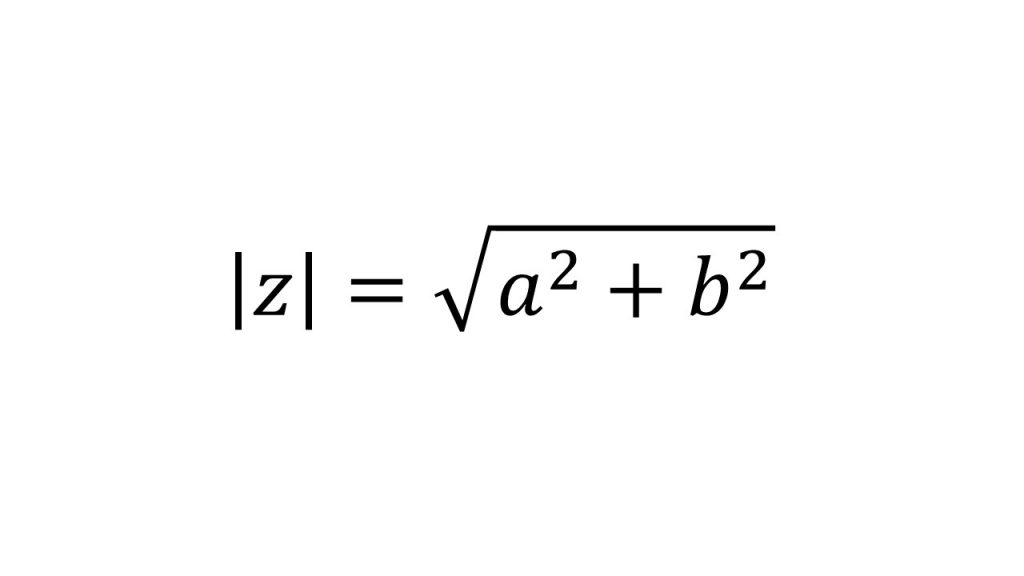
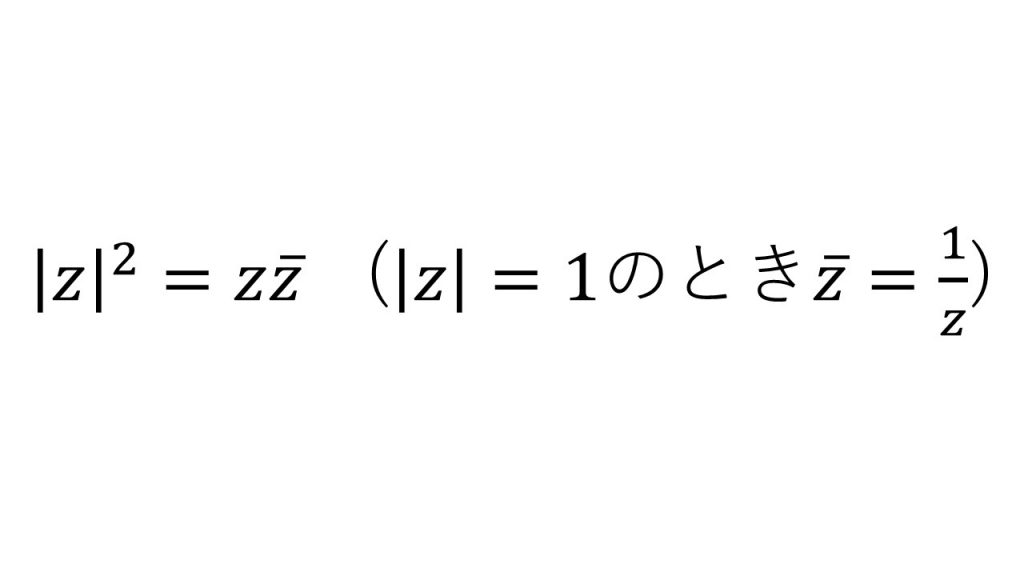
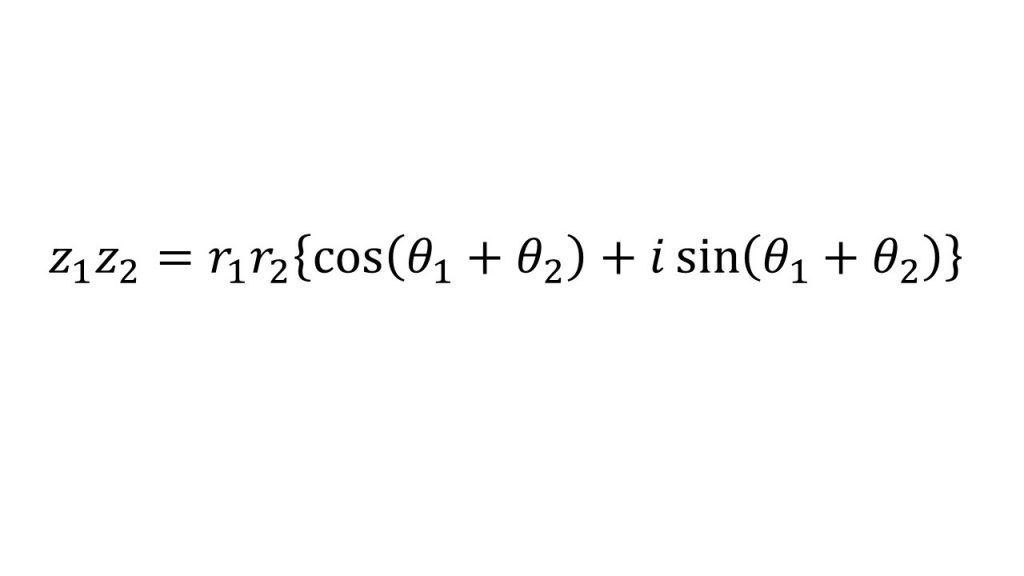
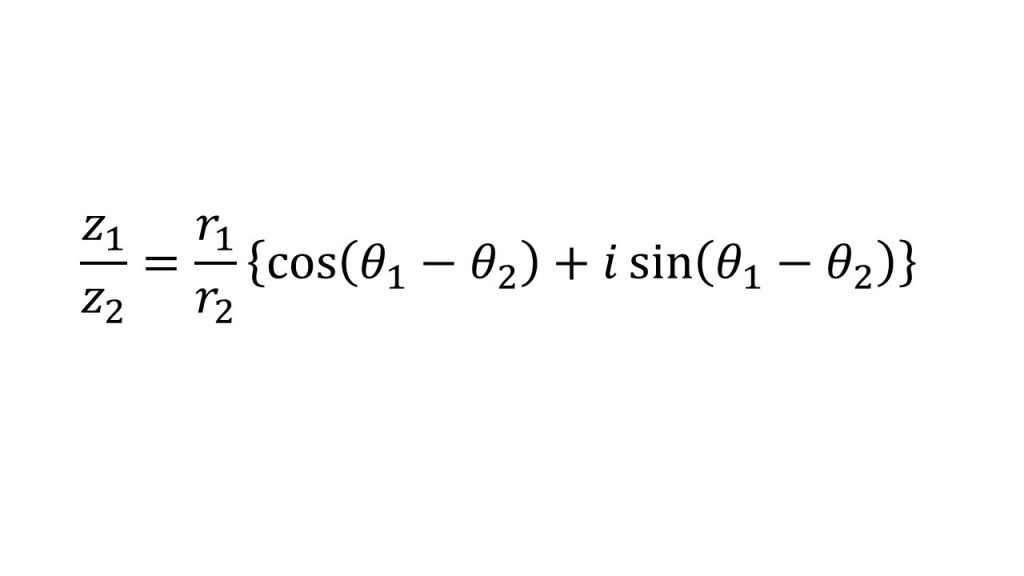
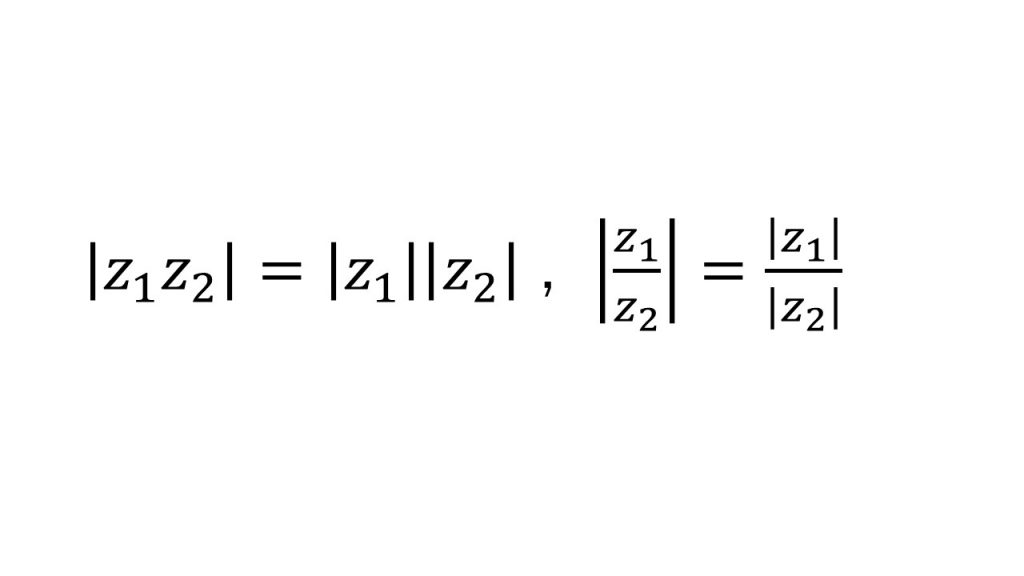
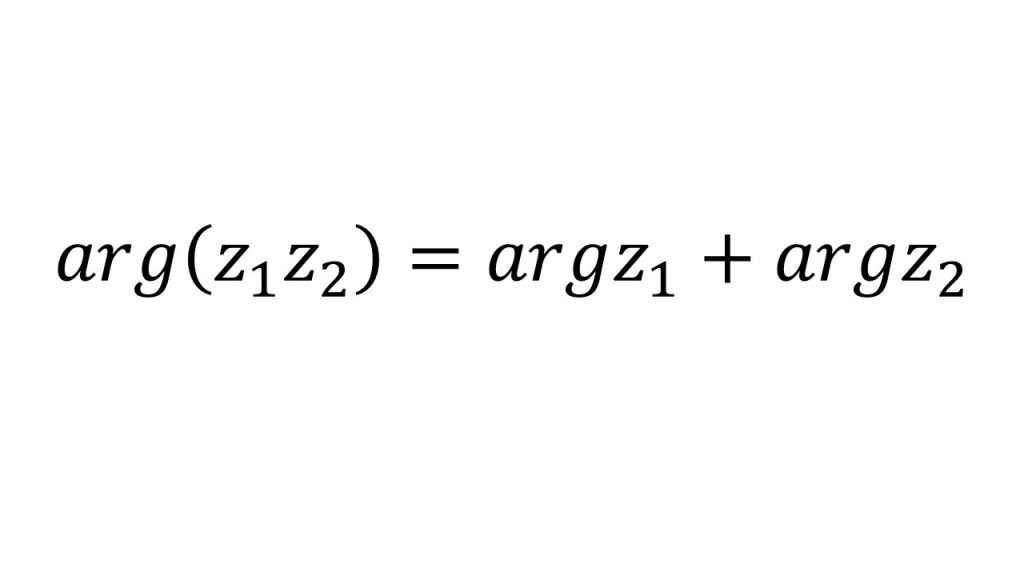
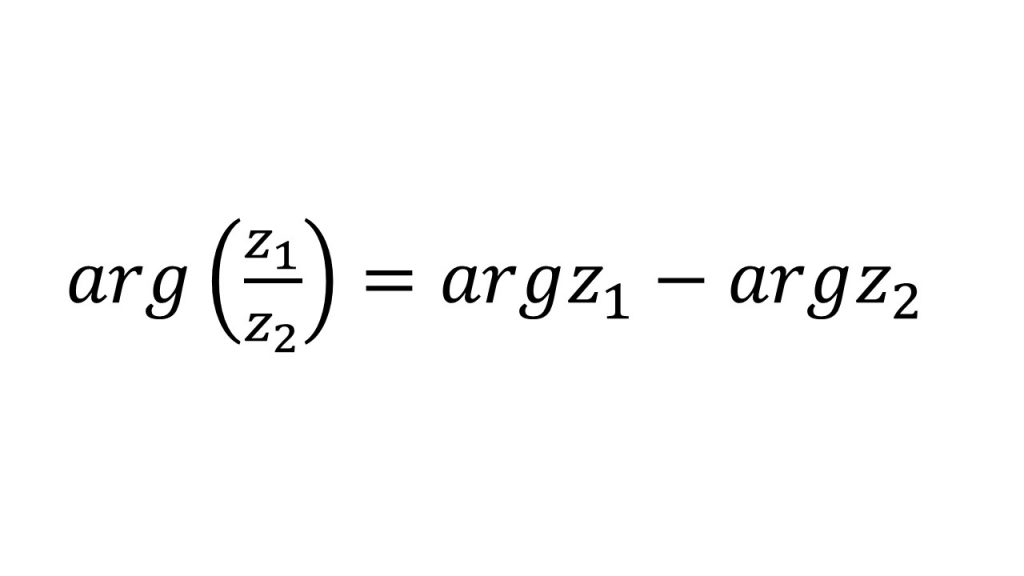
②回転移動
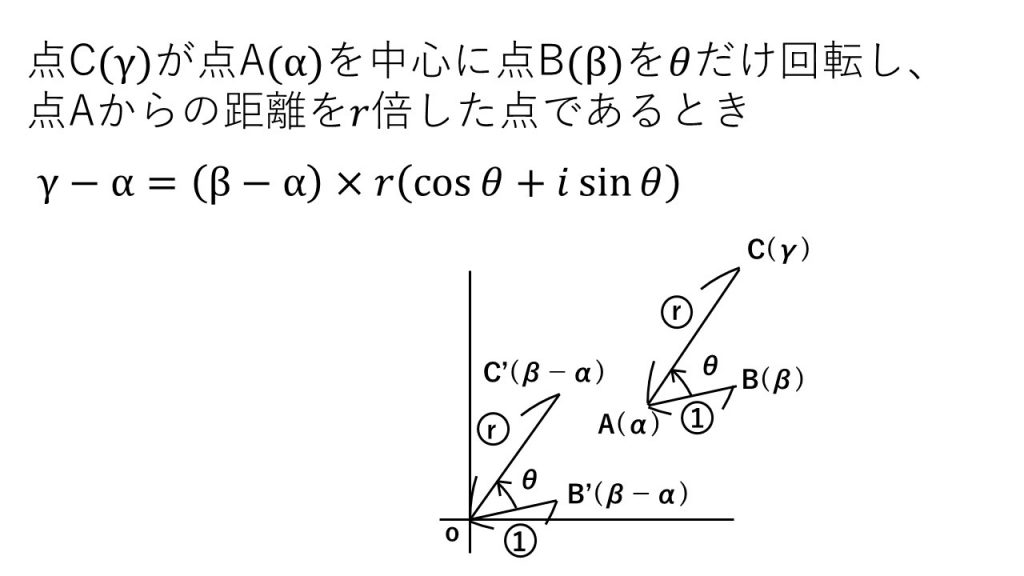
③ド・モアブルの定理

④複素数の相等
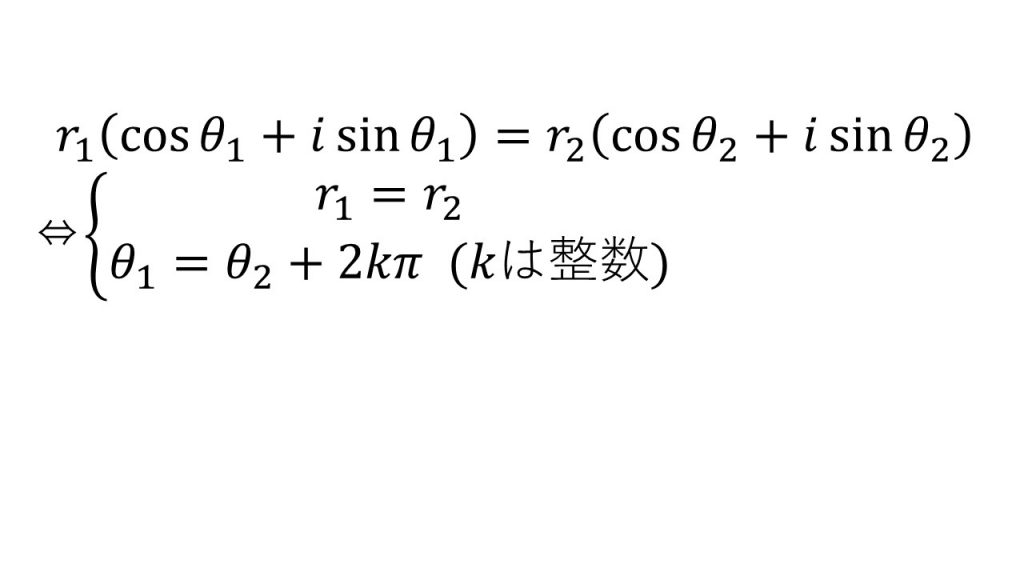
⑤n乗根

⑥複素平面における図形






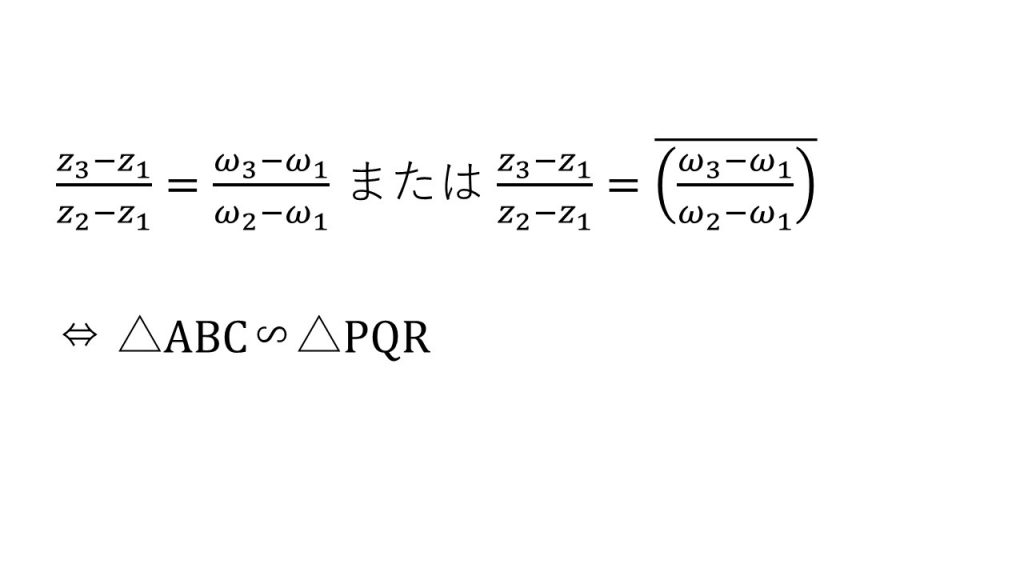



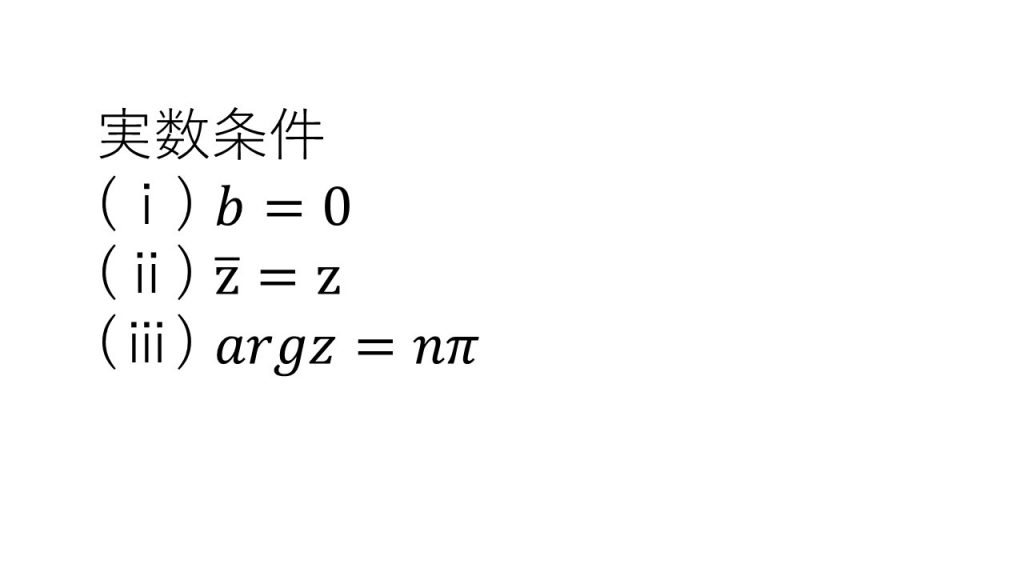

(2)二次曲線
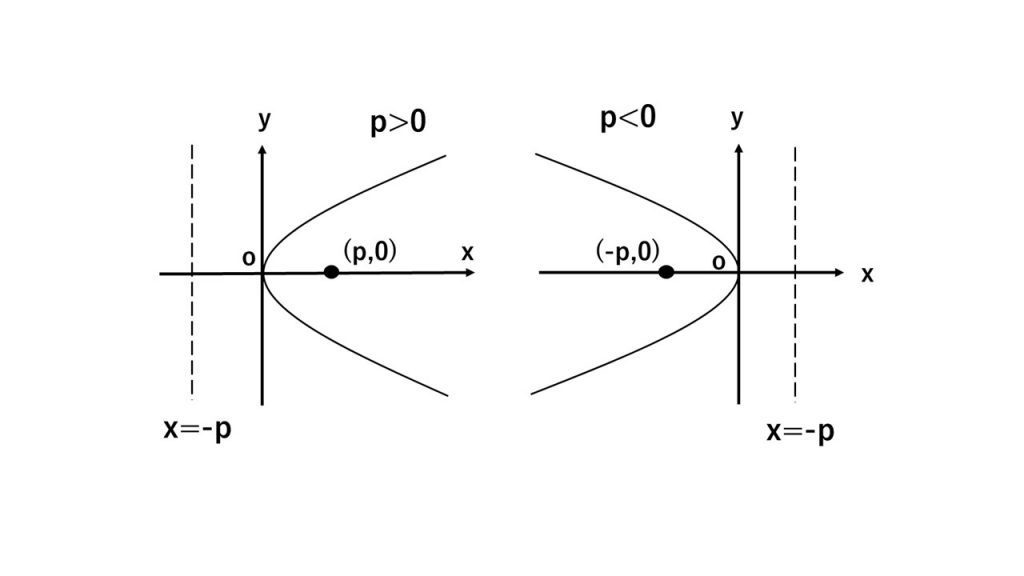
①放物線


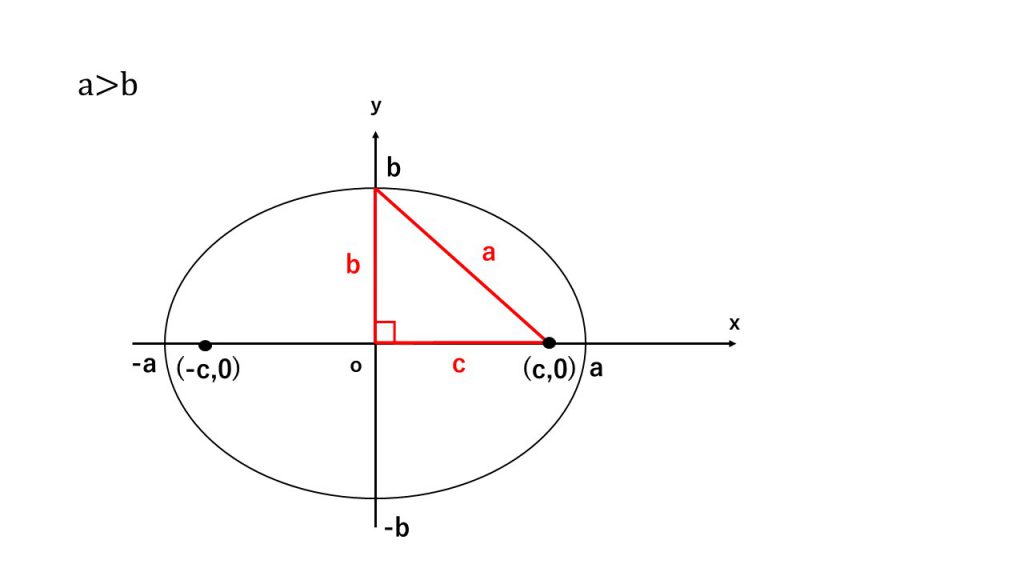
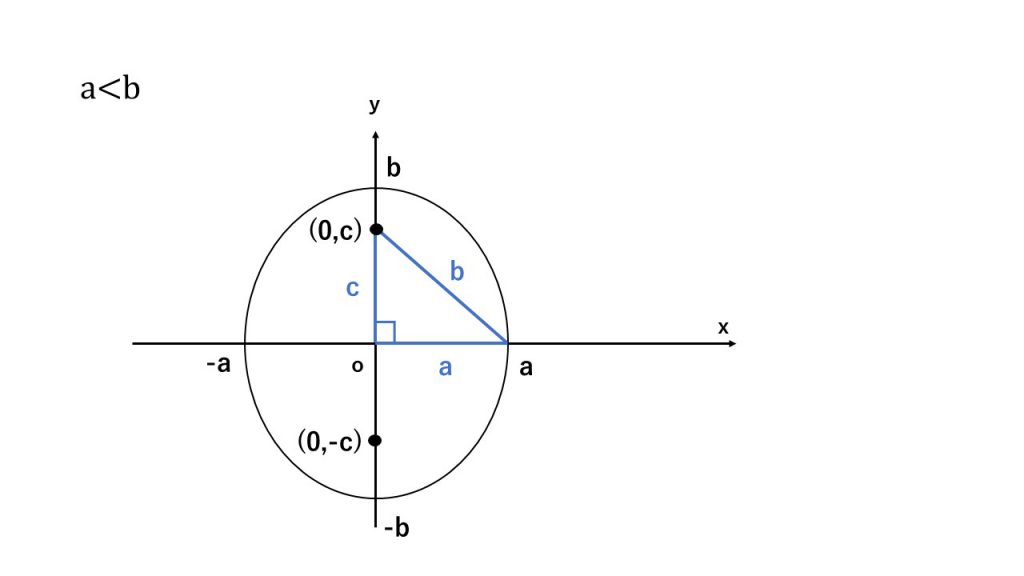
②楕円




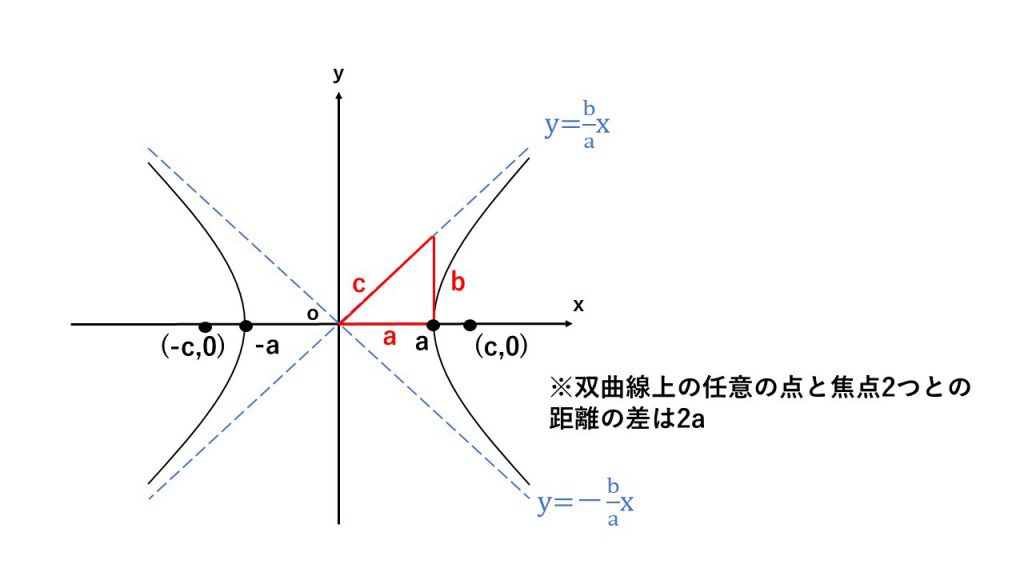
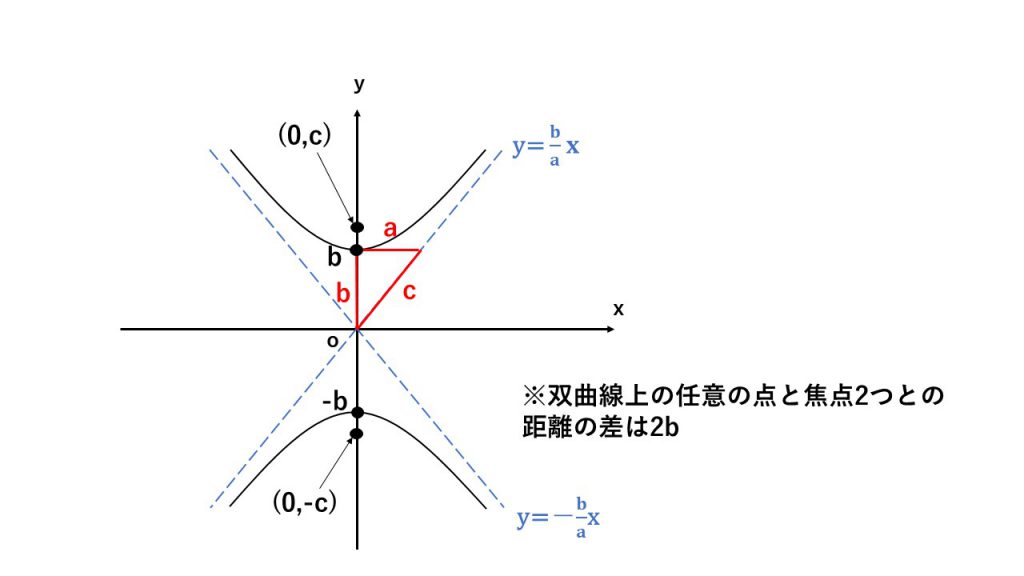
③双曲線


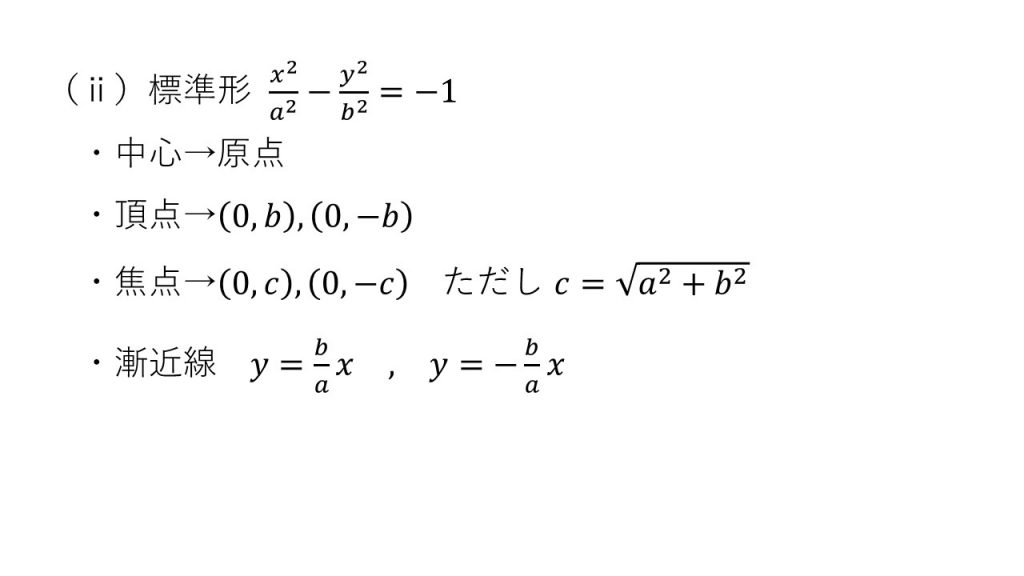
④接線の方程式



(3)数列の極限
①極限があるとは

②極限の不定形

③はさみうちの原理

④追い出しの原理

⑤商の極限

⑥無限等比数列

⑦無限級数



⑧無限等比級数

(4)関数の極限
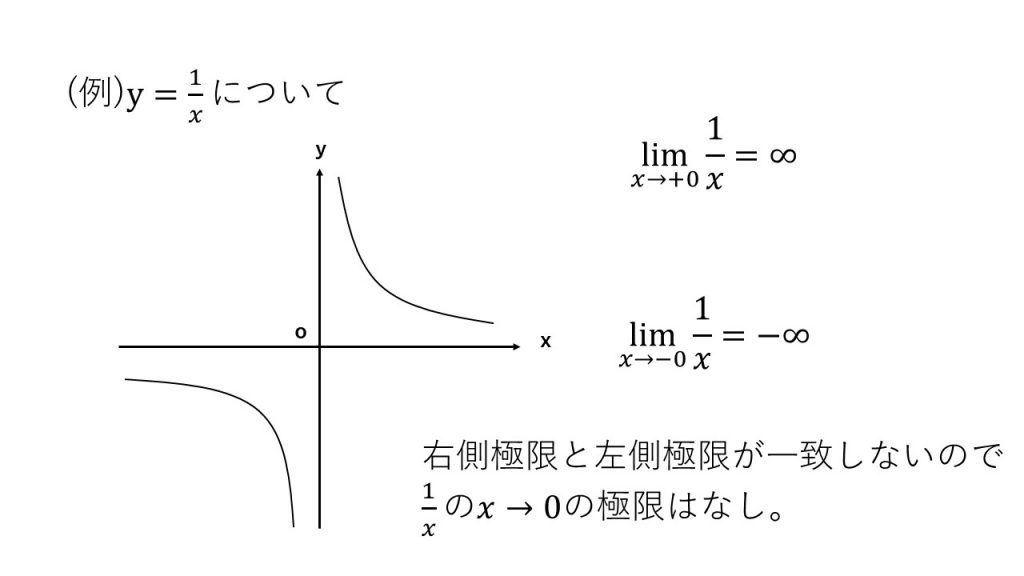
①片側極限

②はさみうちの原理

③三角関数の極限
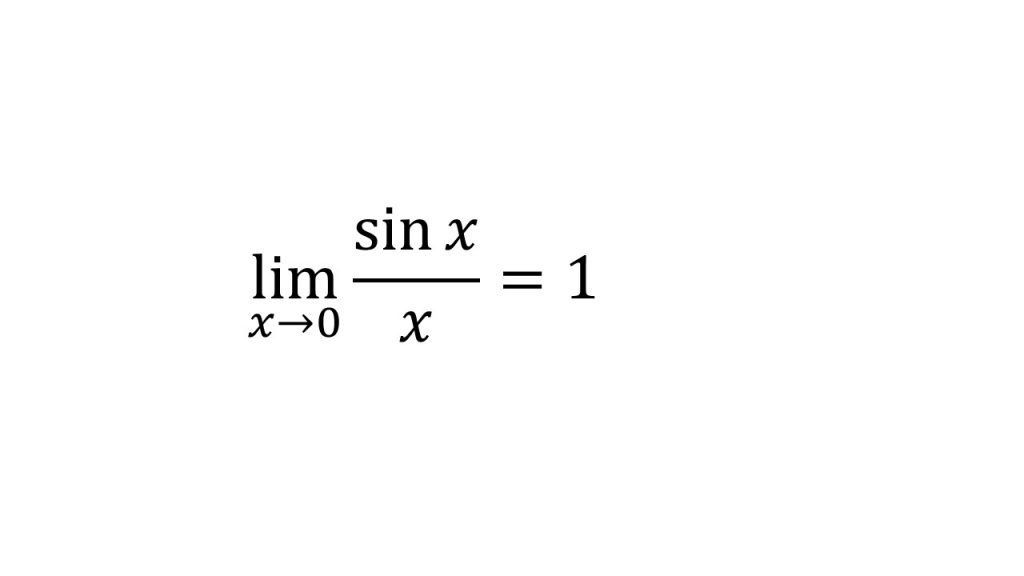
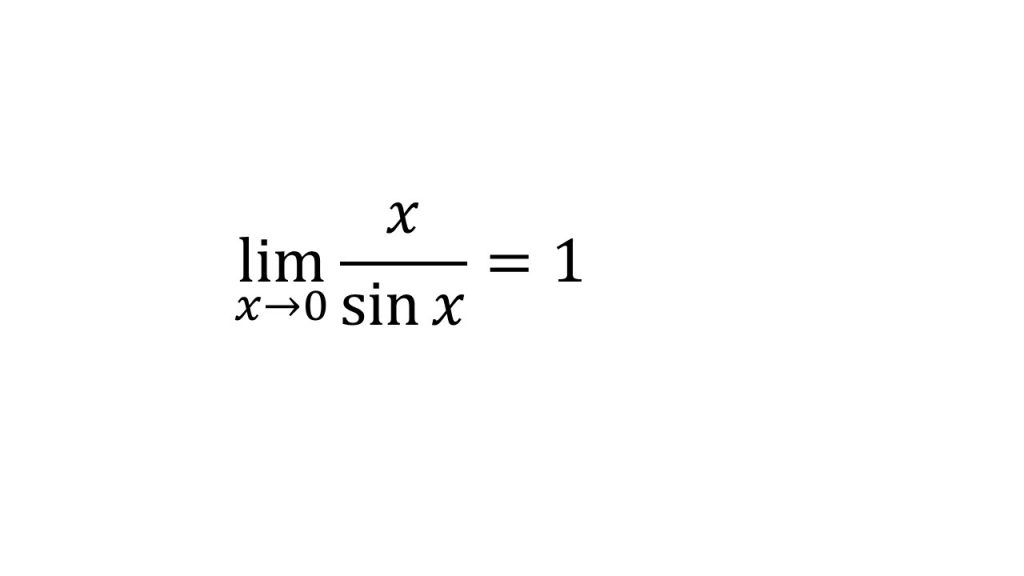
④自然対数の底e
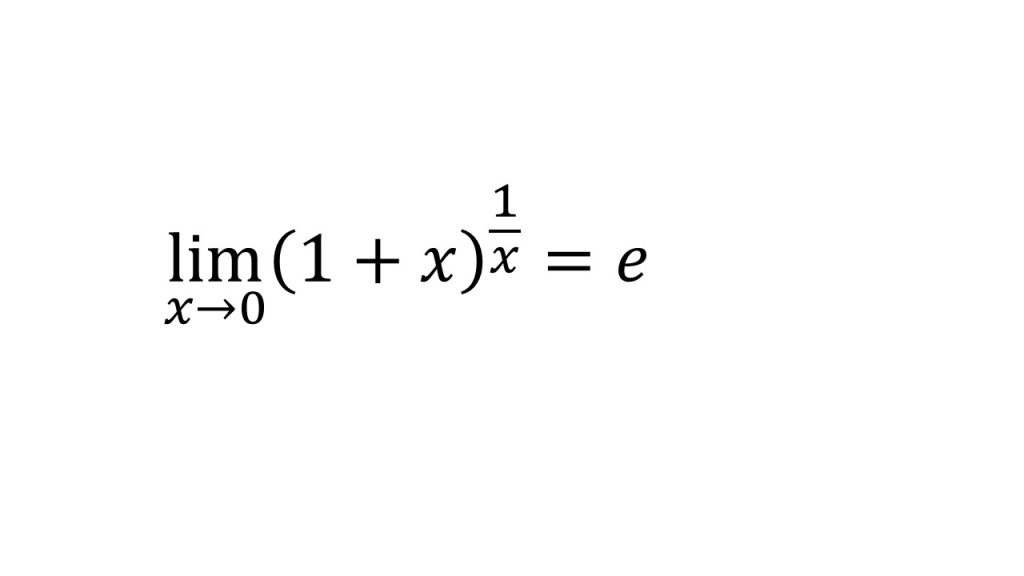
※これが自然対数の底eの定義。以下の3つの式はこれを用いて導かれる。
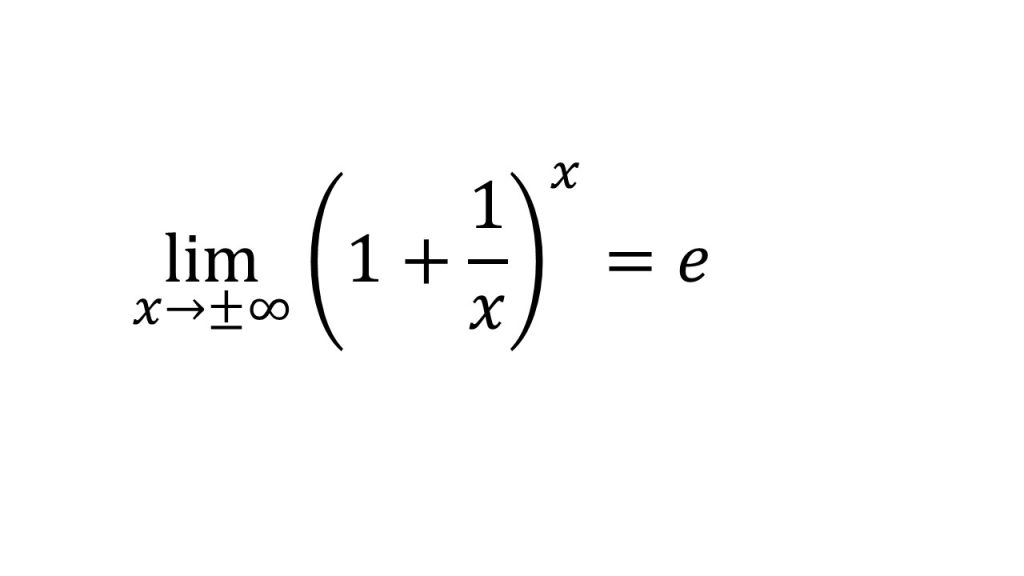

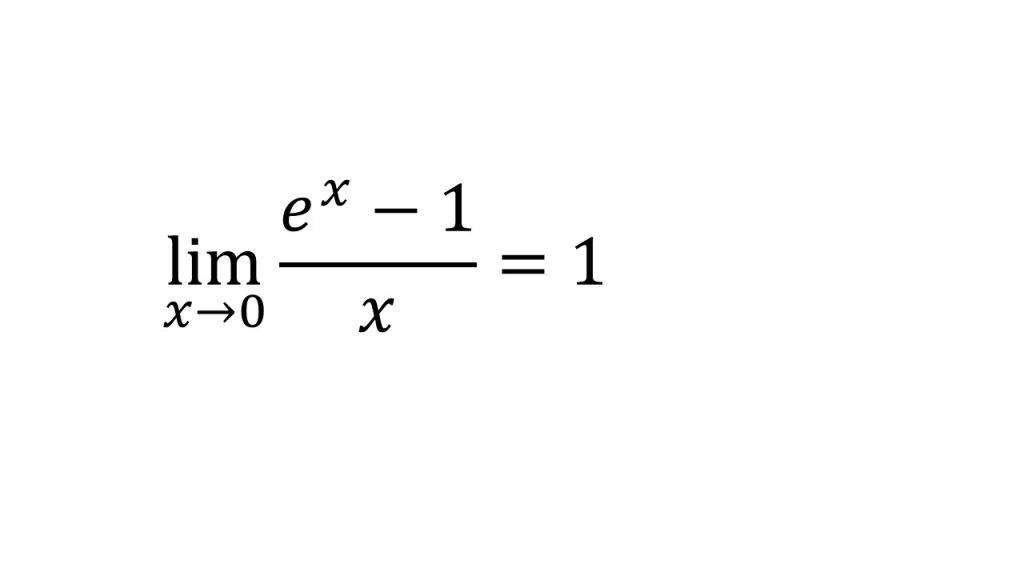
⑤関数の連続性


⑥中間値の定理

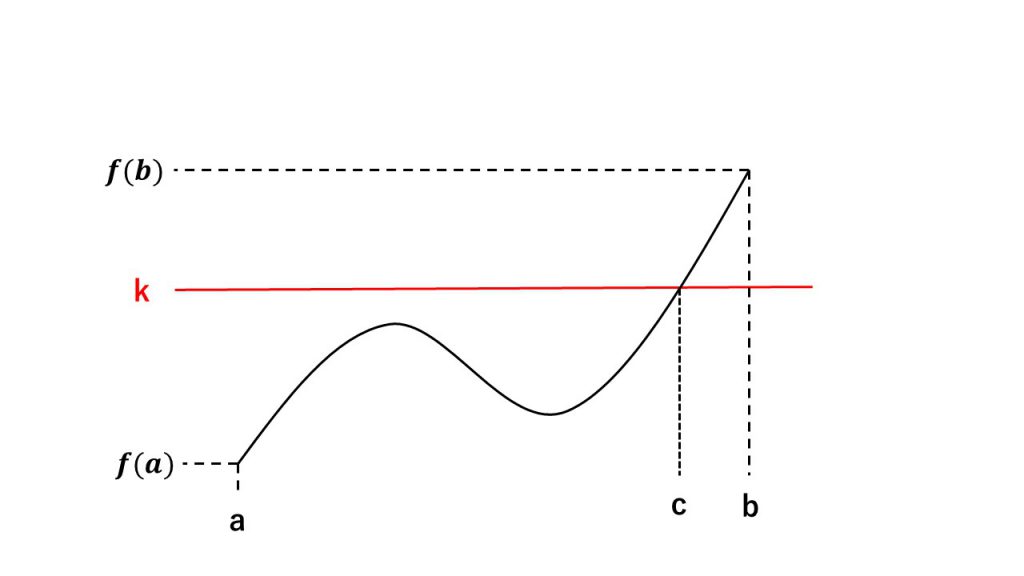
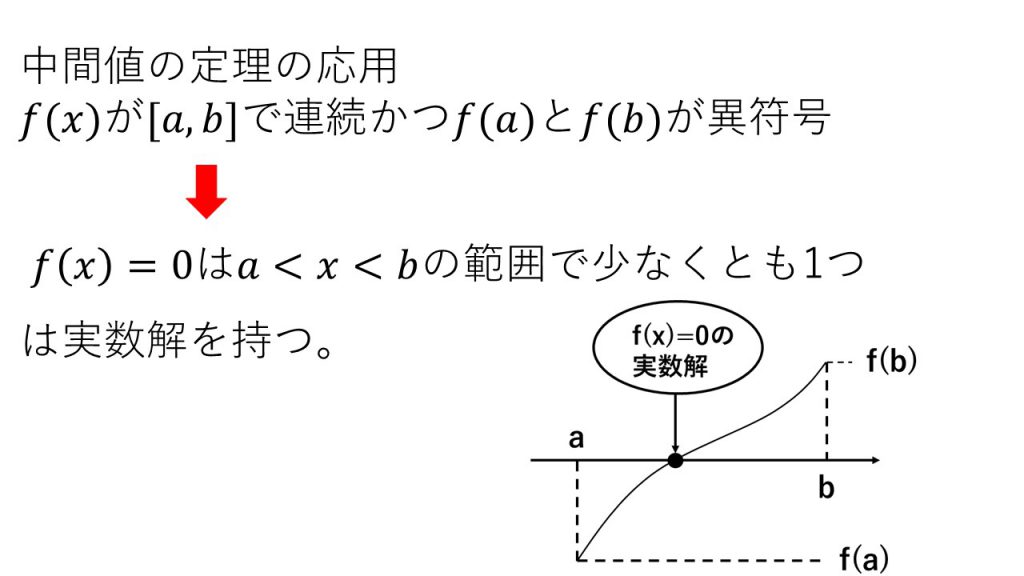
(5)微分法の計算公式
①xαの微分
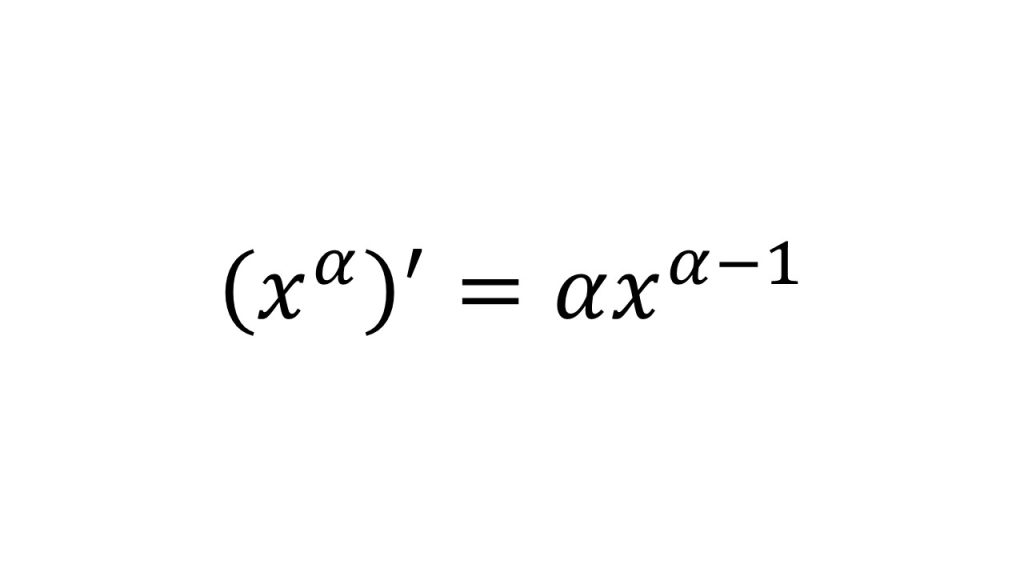
※αは実数で成り立つ(負の数でも、分数でも、無理数でも成り立つ)。
②積の微分
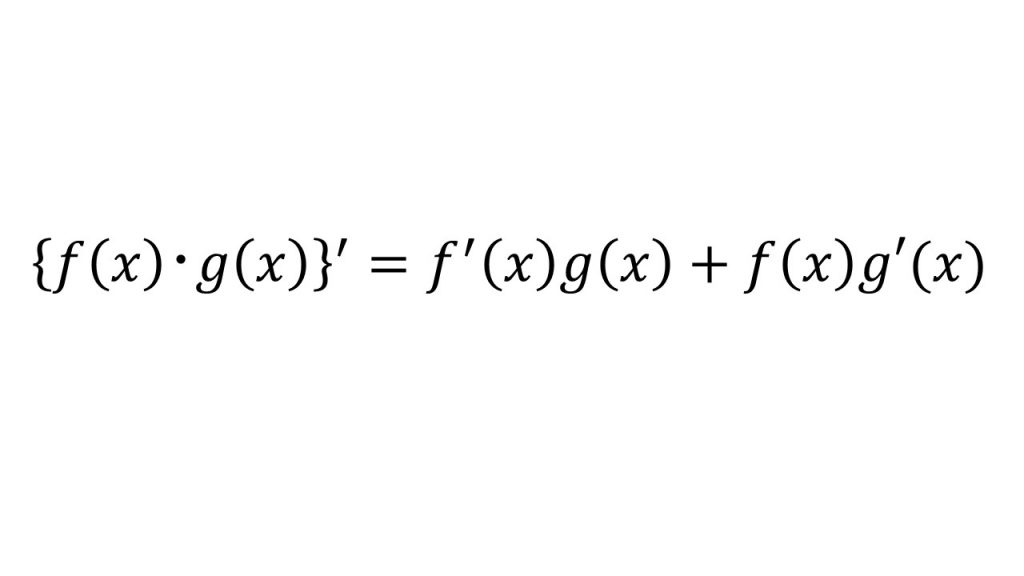
③商の微分
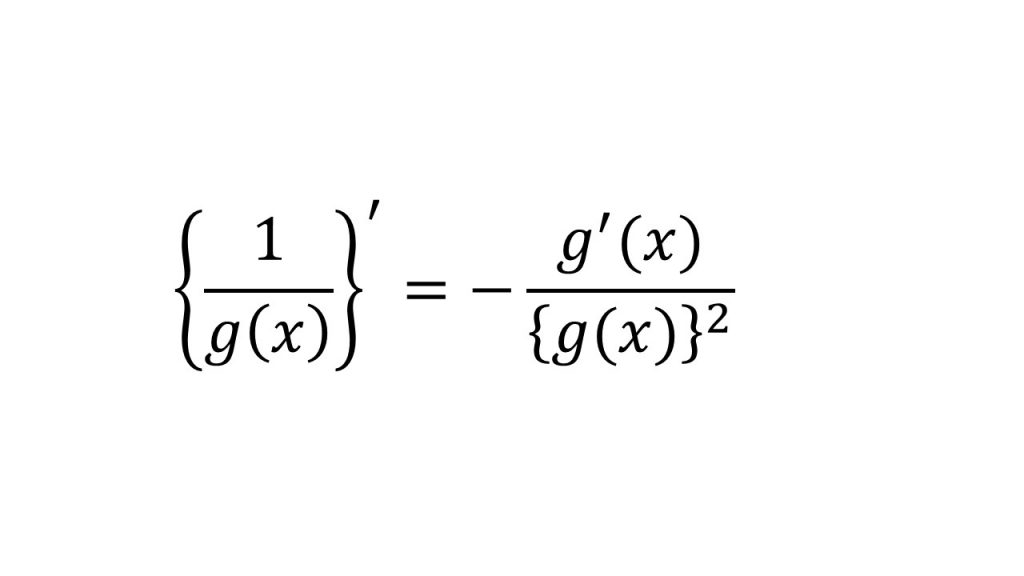
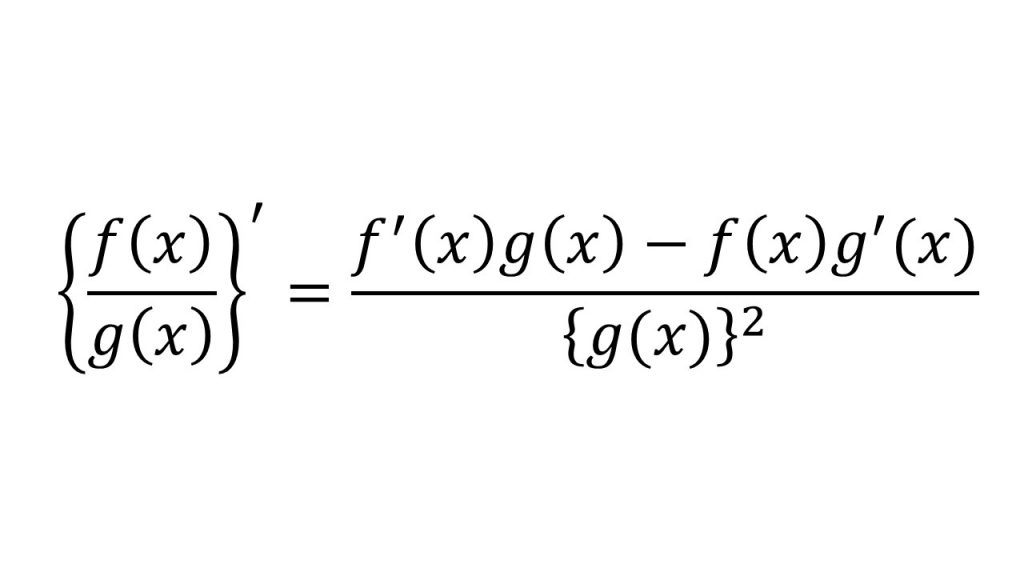
④三角関数の微分
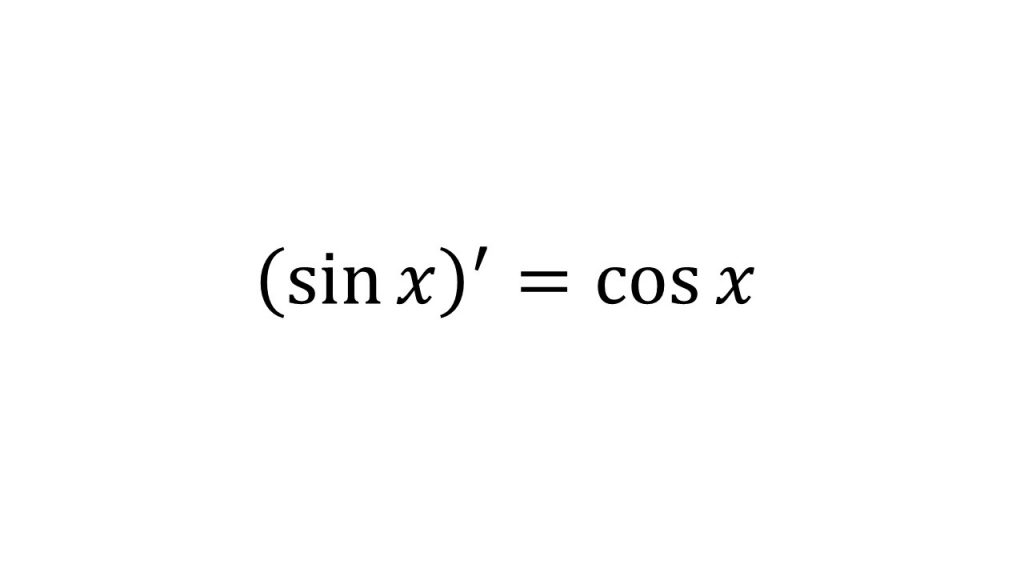
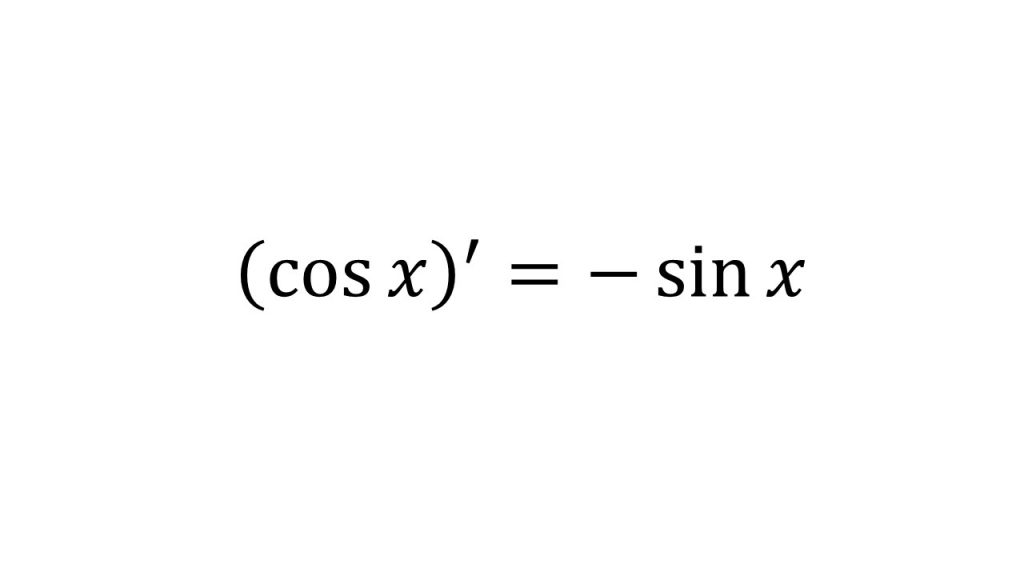
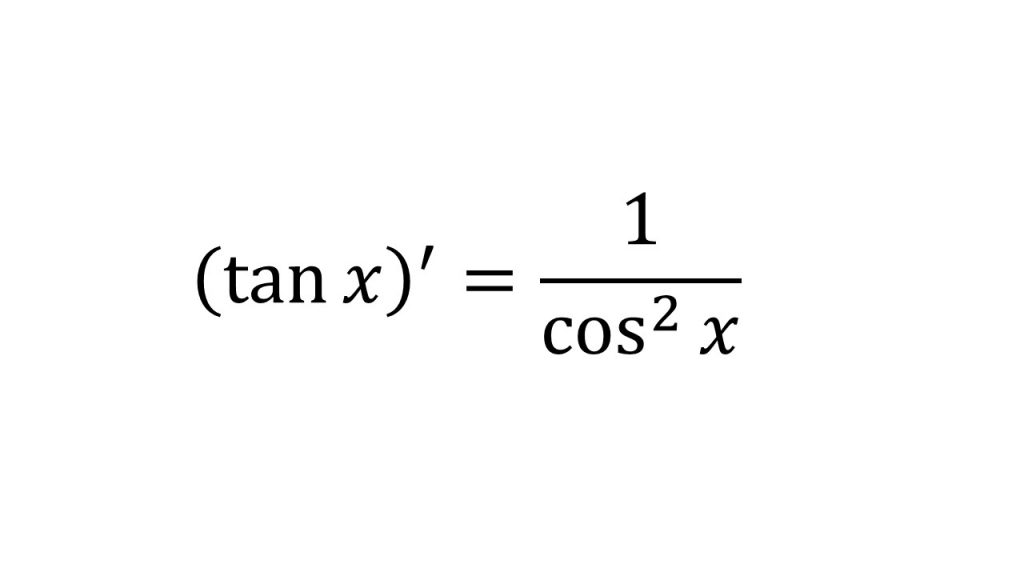
⑤指数関数の微分
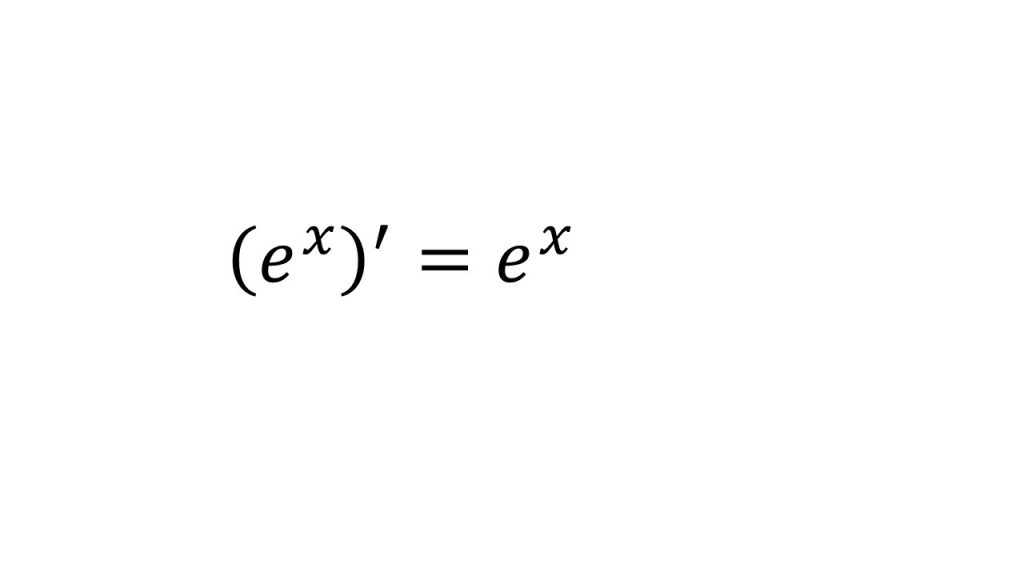
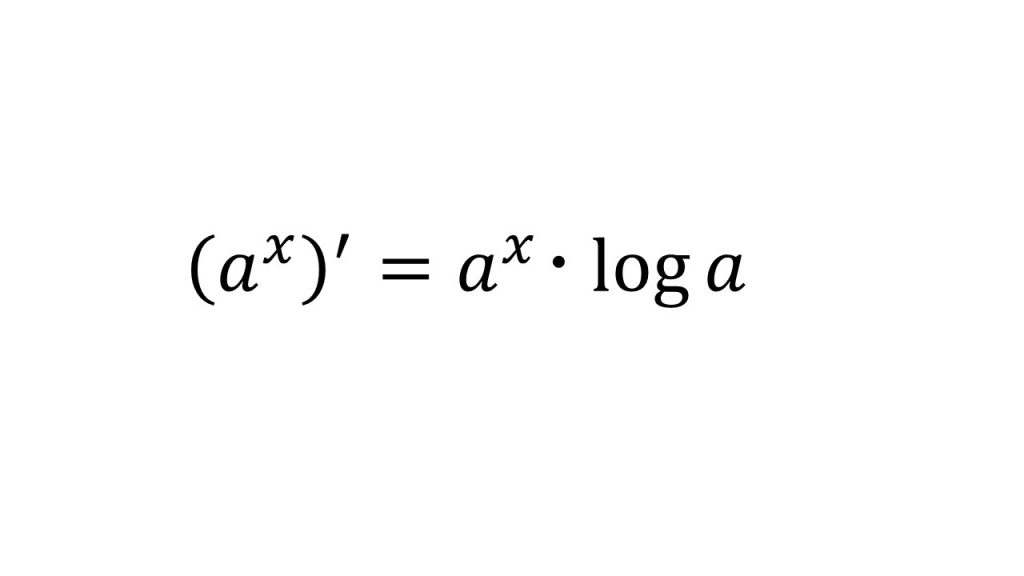
⑥対数関数の微分

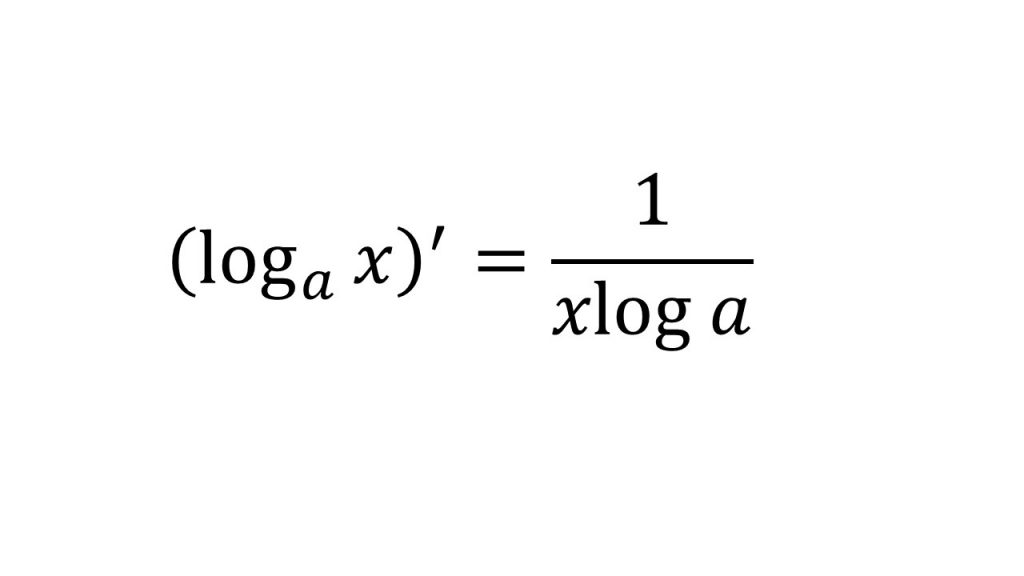
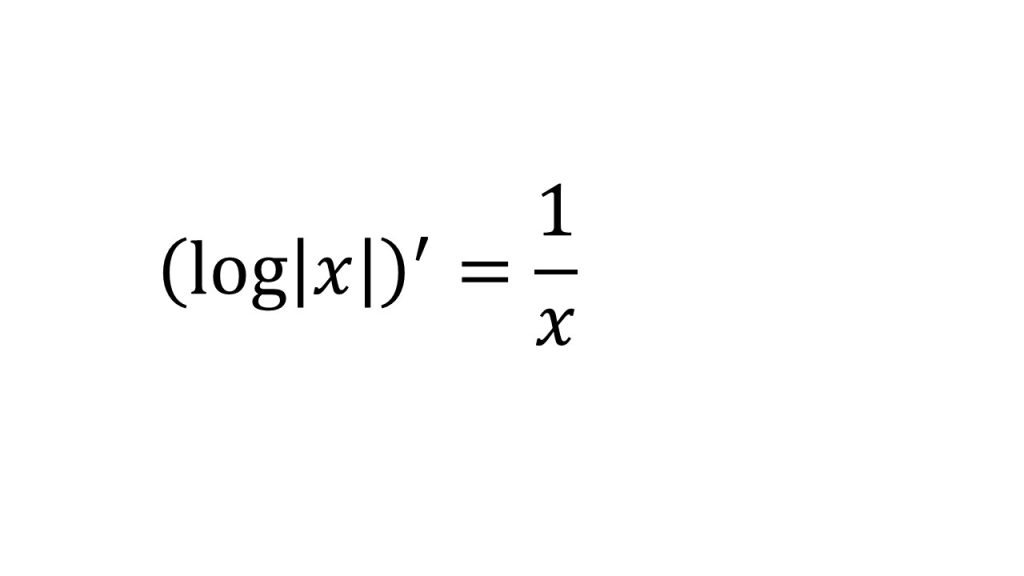
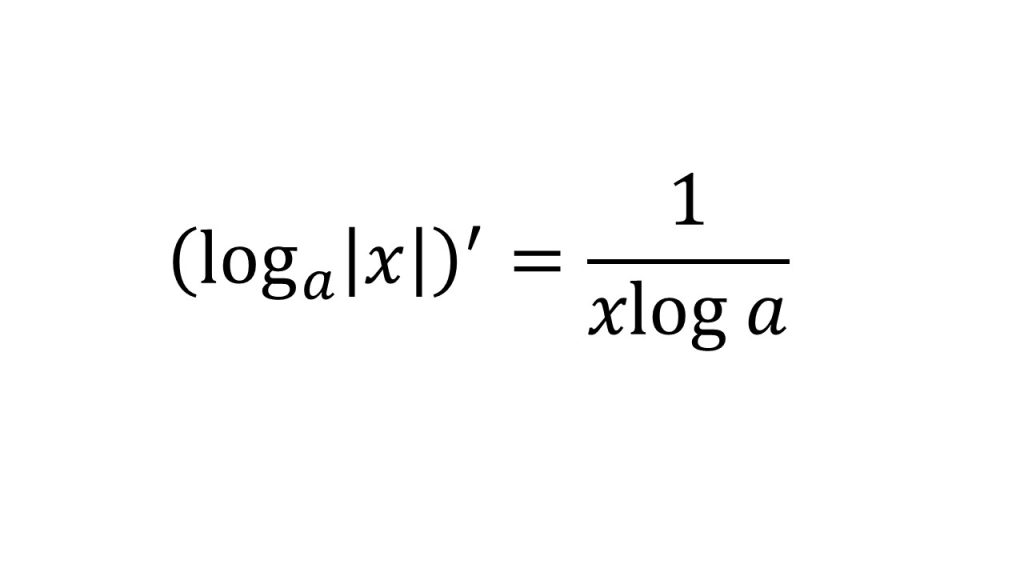
⑦合成関数の微分

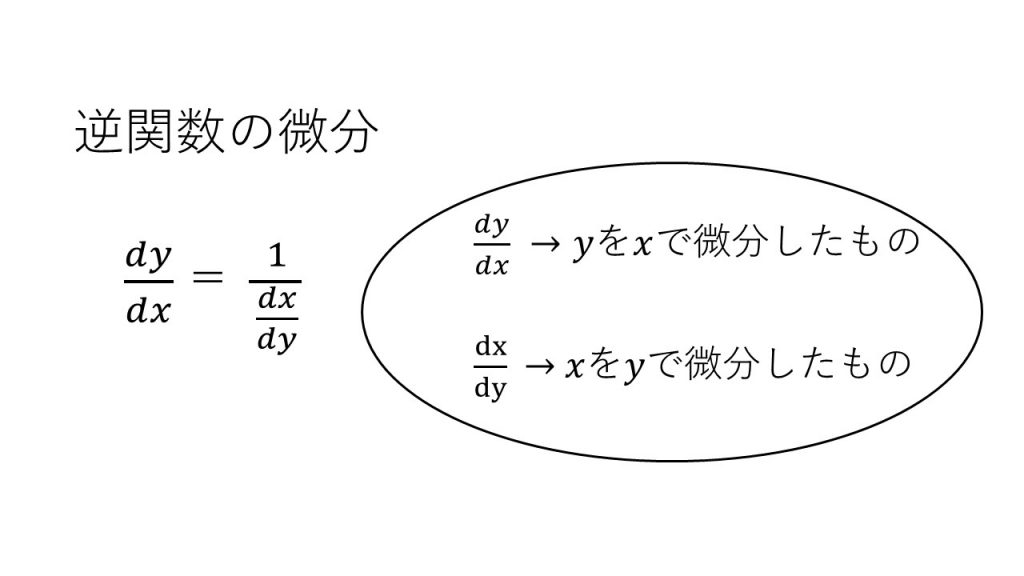
⑧逆関数の微分

⑨対数微分法
【手順】
- 両辺が正であることを確認する。正であることを確認できない場合は、両辺に絶対値をつける。(対数の真数は正でないといけないので)
- 両辺の自然対数をとる。
- 両辺をxで微分する。(logy)’=y’/yであることに注意(合成関数の微分)。
- 両辺にyをかけて、y’=の形にする。yに元の式を代入するのを忘れないように!
【使いどころ】
- 累乗の積や商で表された関数の微分
- (xの式)xの式のように指数で困ったとき
※対数にすることで、積が和に、商は差に、p乗はp倍にすることができることを利用する。対数の公式についてはこちら→対数公式
(6)微分法の応用
①接線の方程式

②法線の方程式

※法線とは……点Pにおける法線とは、点Pを通り、Pにおける接線と垂直に交わる直線のこと
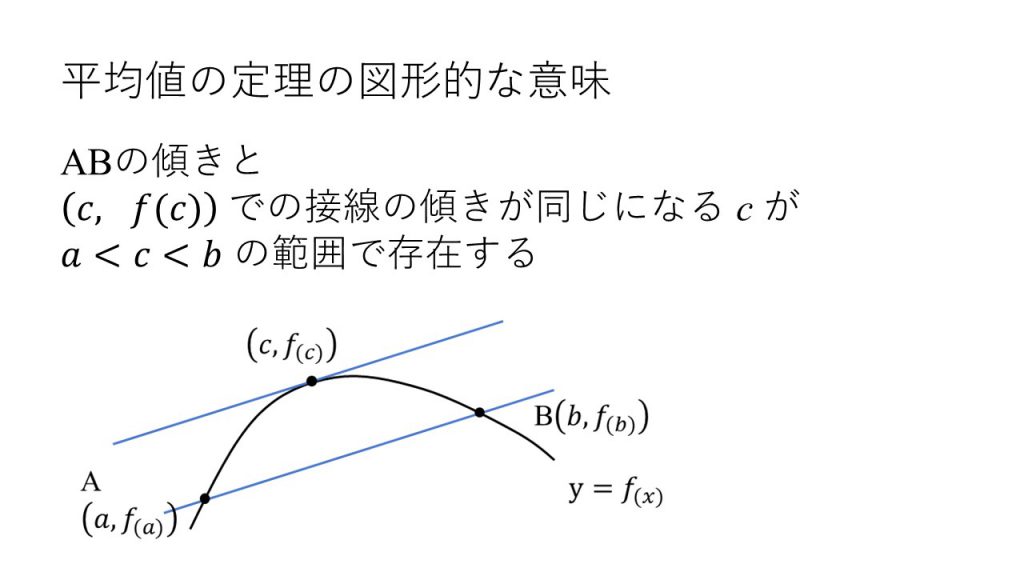
③平均値の定理

④関数の増減

⑤関数の凹凸

⑥関数の極大値と極小値

⑦媒介変数で表された関数の微分

⑧漸近線
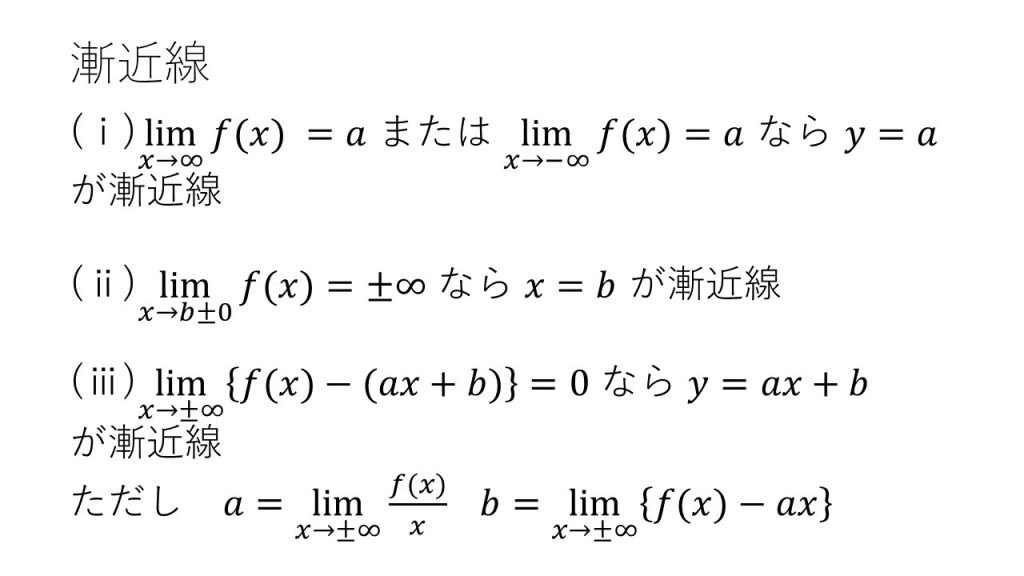
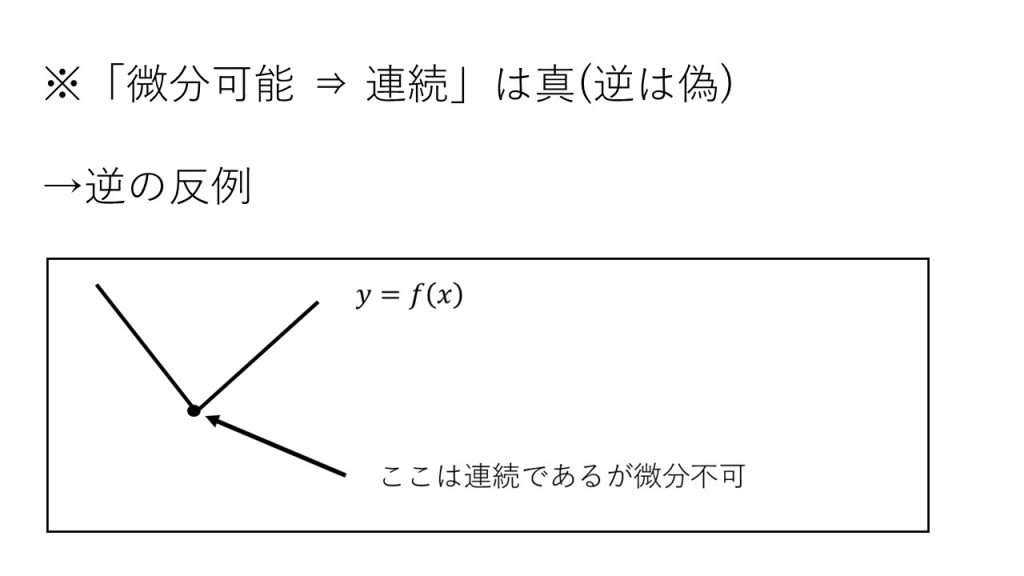
⑨微分可能性

(7)積分公式
①整式の不定積分
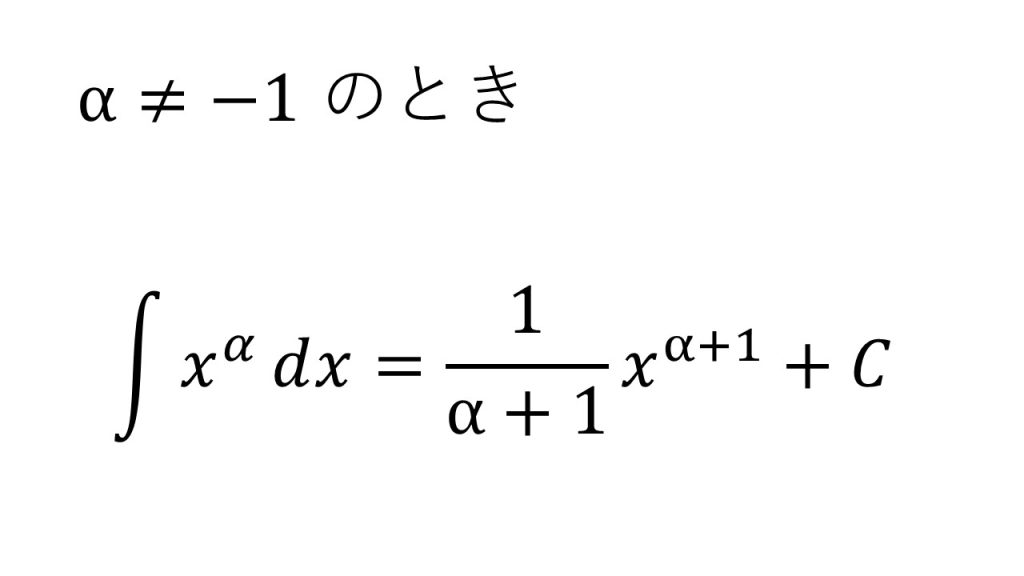
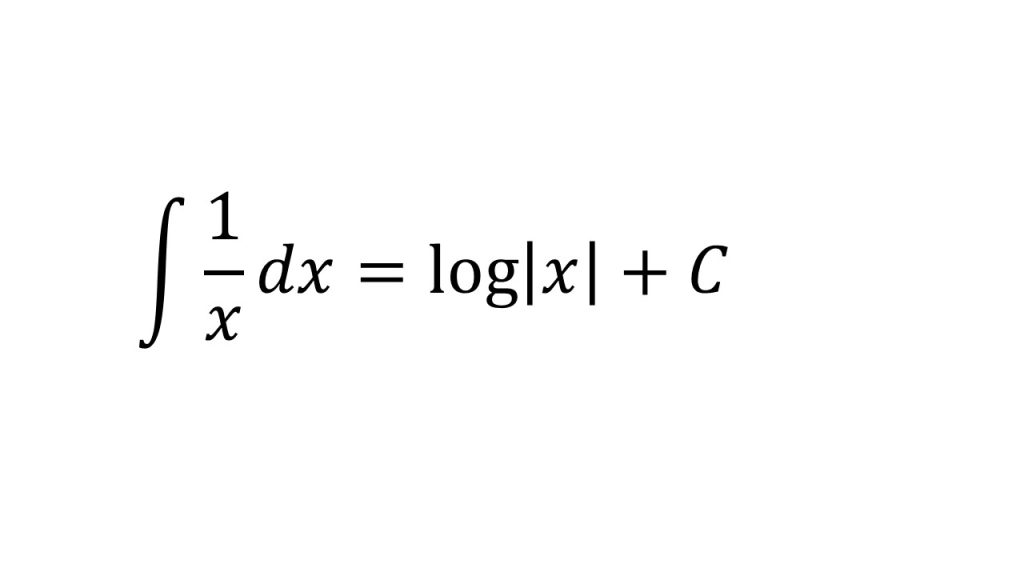
②三角関数の不定積分
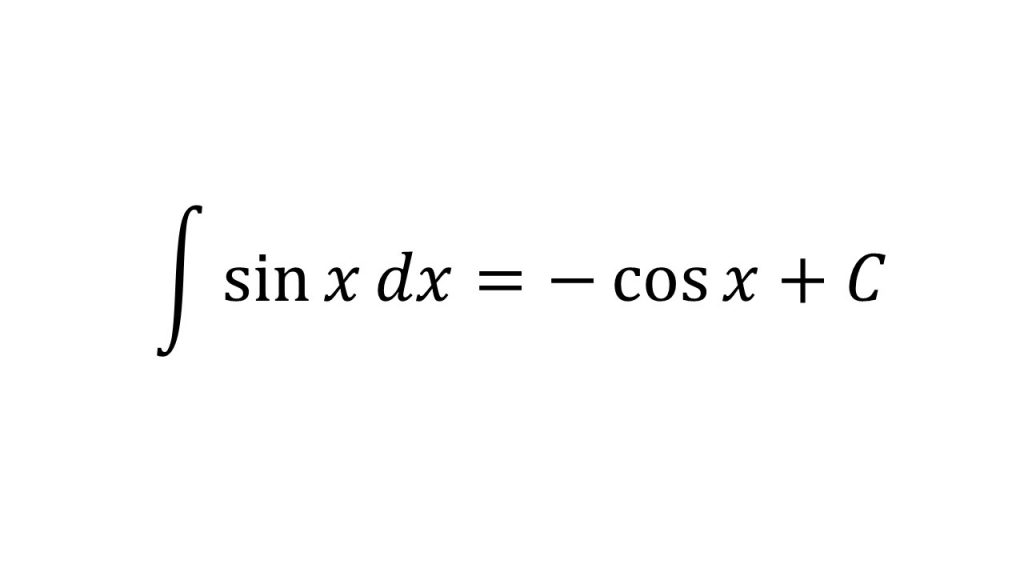
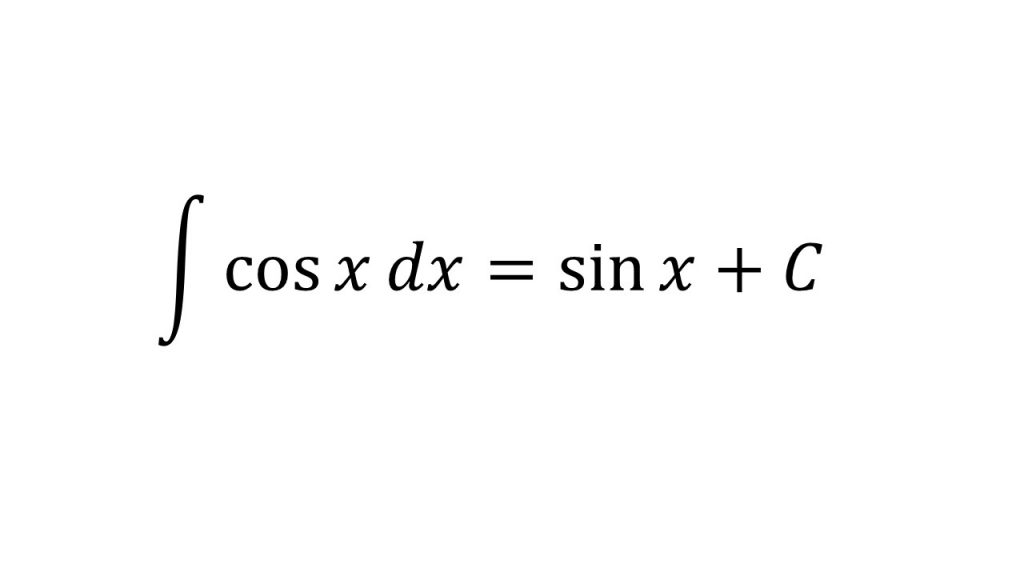
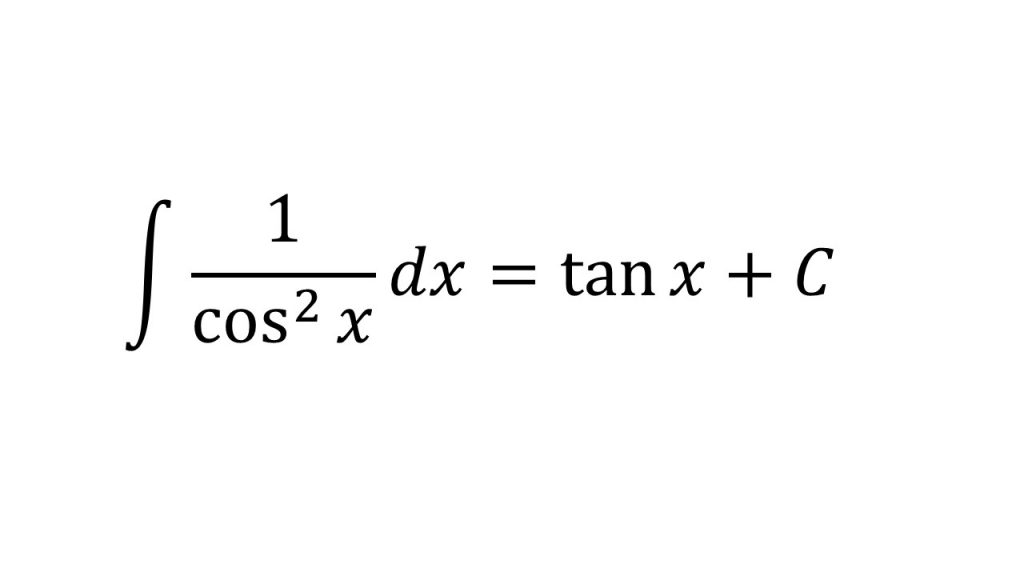
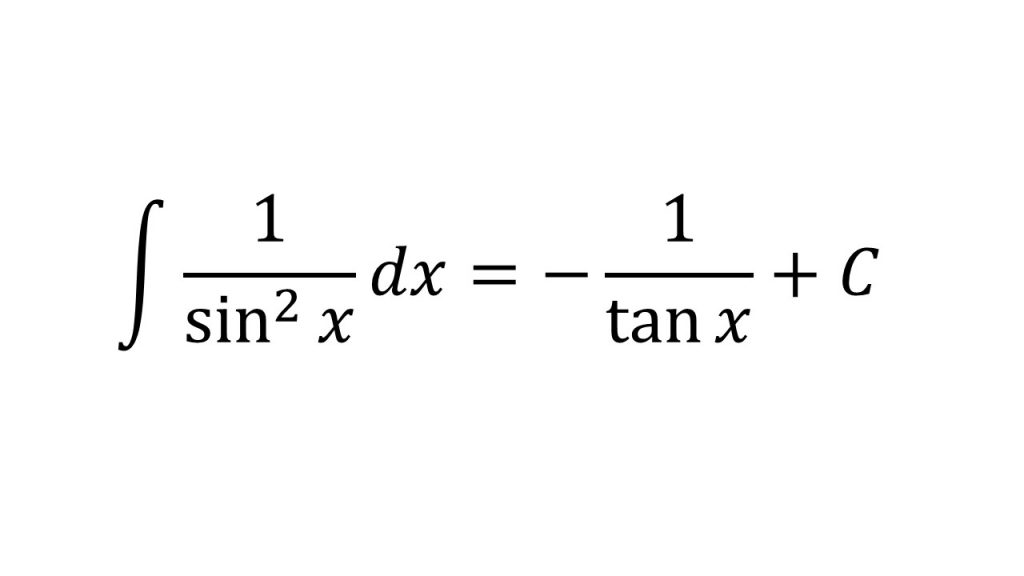
③指数関数の不定積分
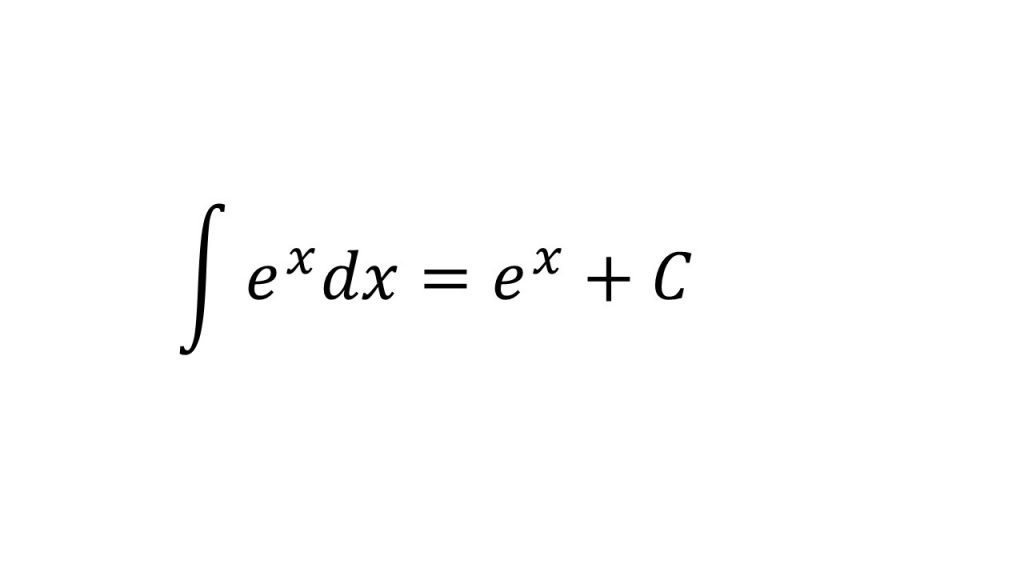
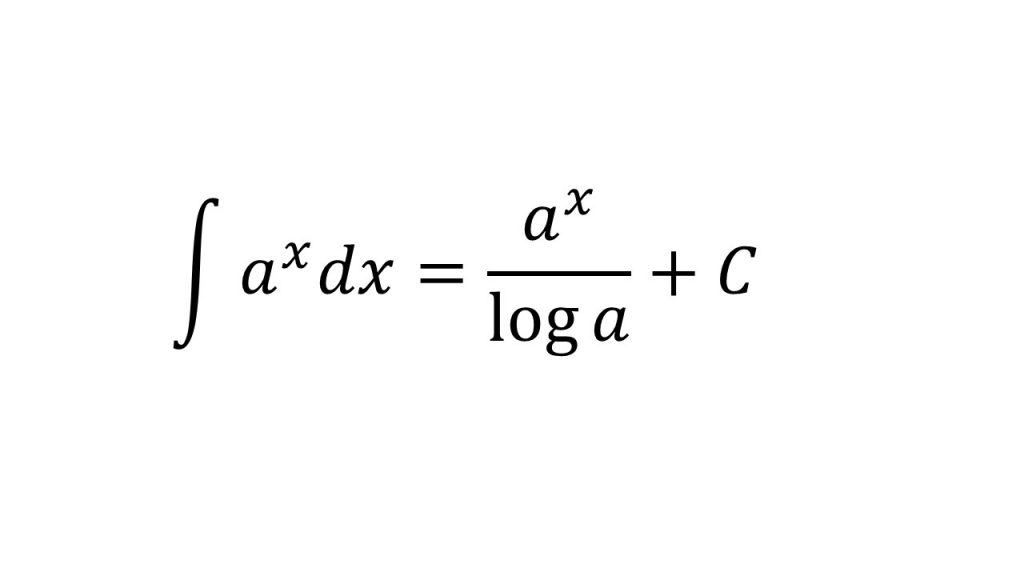
④置換積分法
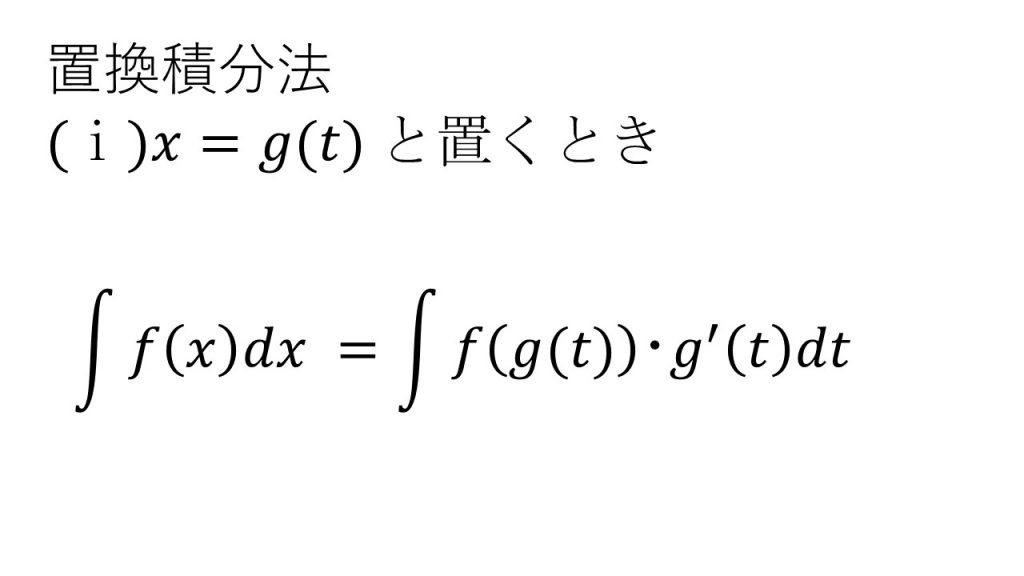
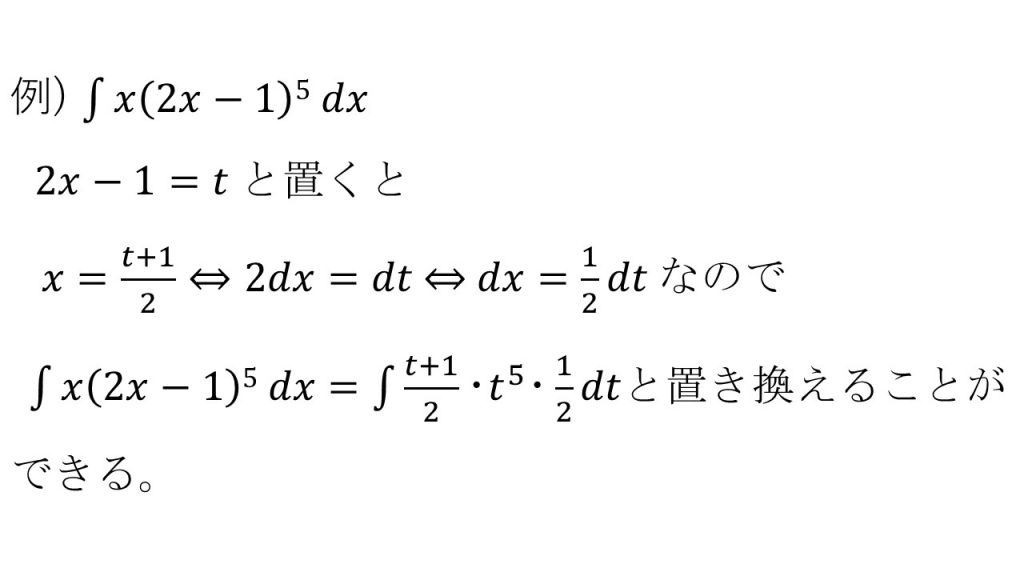
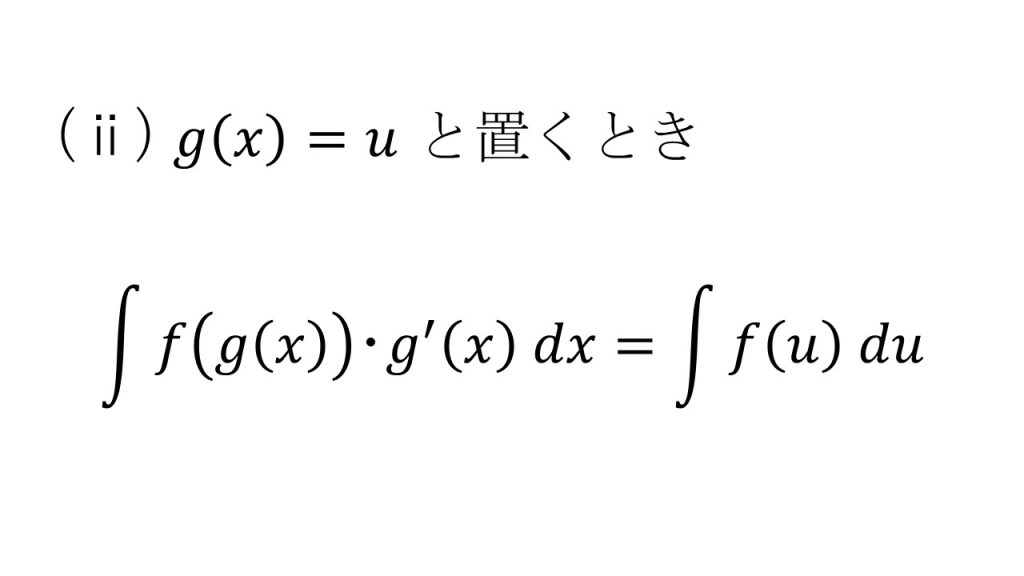

⑤特殊な置換を使って求める不定積分
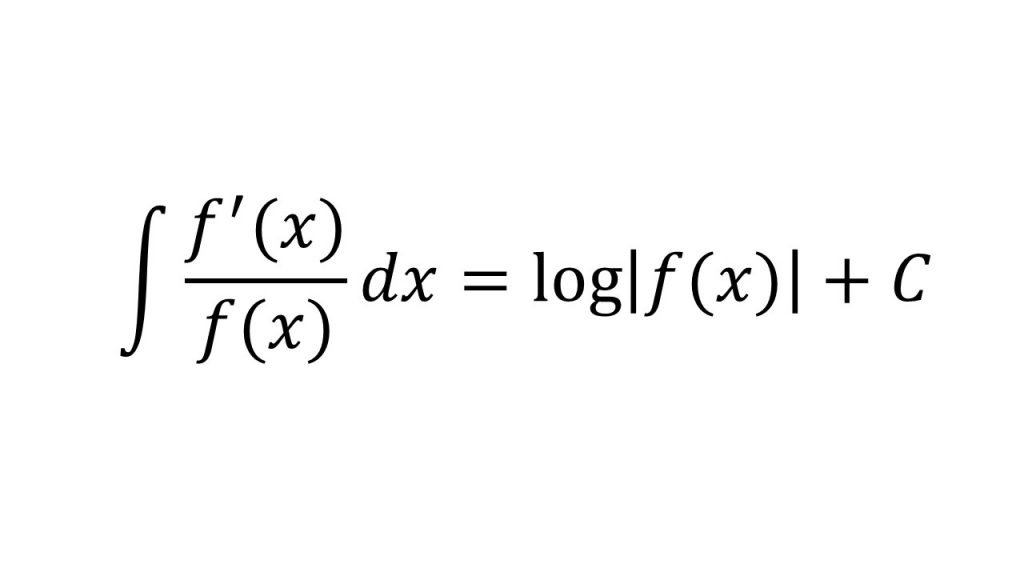
※公式として覚えてしまおう。
⑥部分積分法
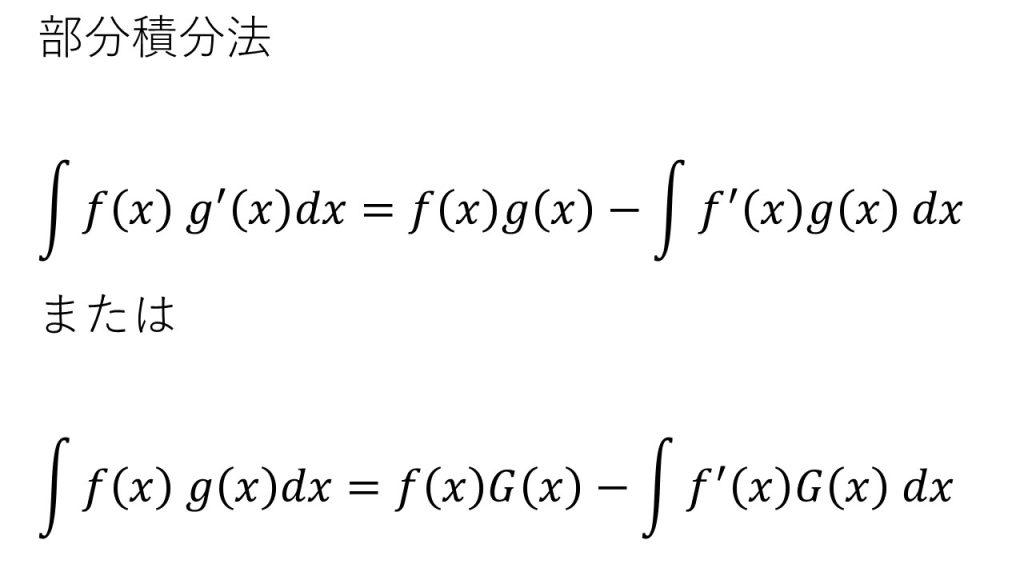
※積分する関数が異なる関数の積の形となっているときに用いることが多い。
※微分すると簡単になるものをf(x)、指数関数や三角関数など(微分してもあまり形が変わらないもの)をg(x)とするとやりやすくなることが多い。
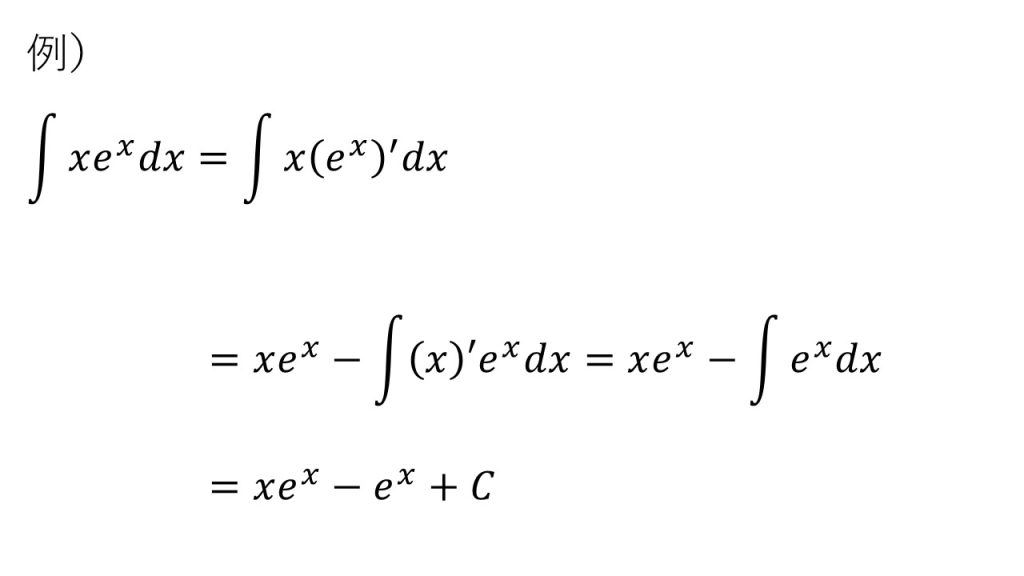
⑦三角関数で変形が必要な積分

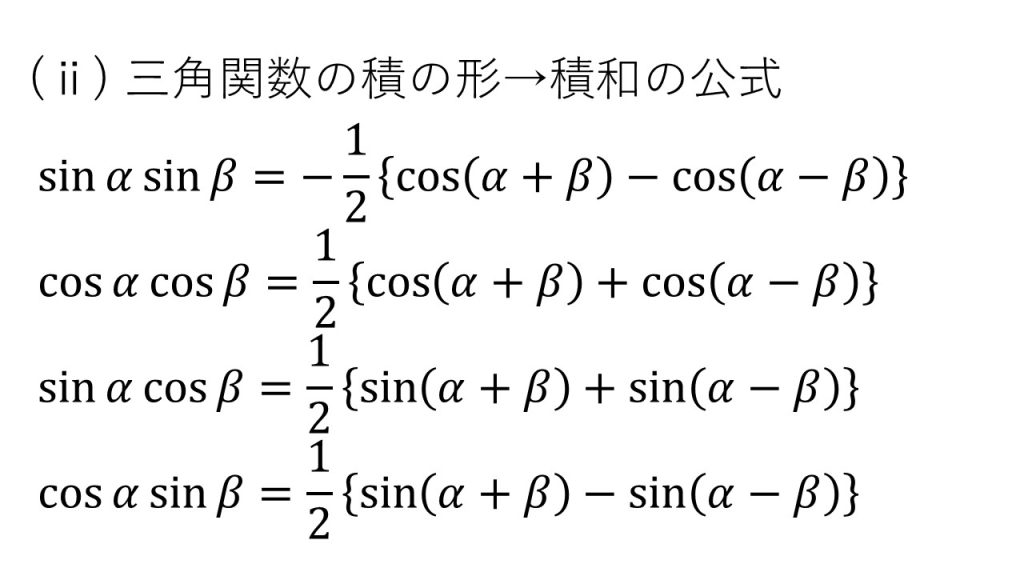
⑧特殊な置換積分(定積分)

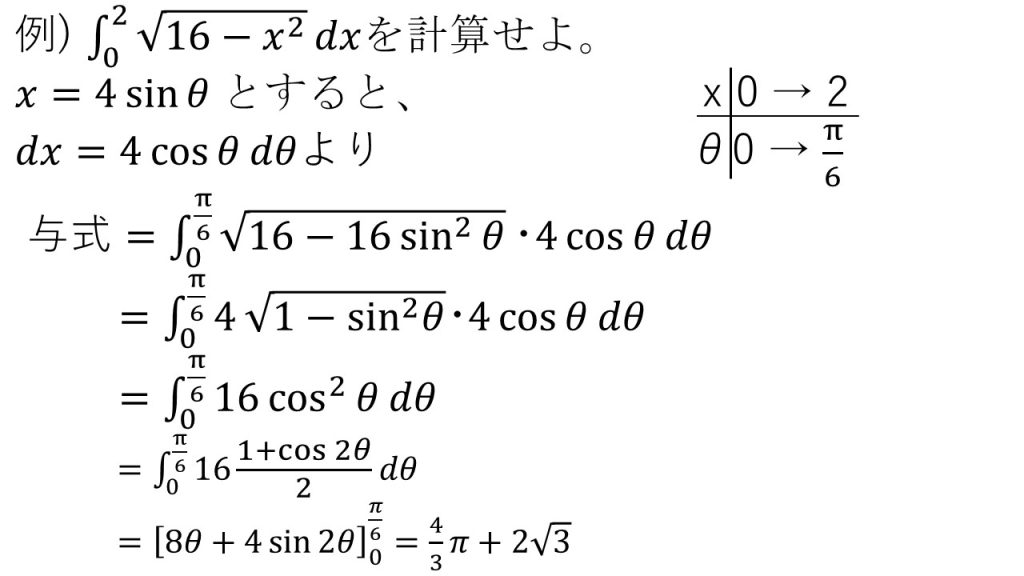

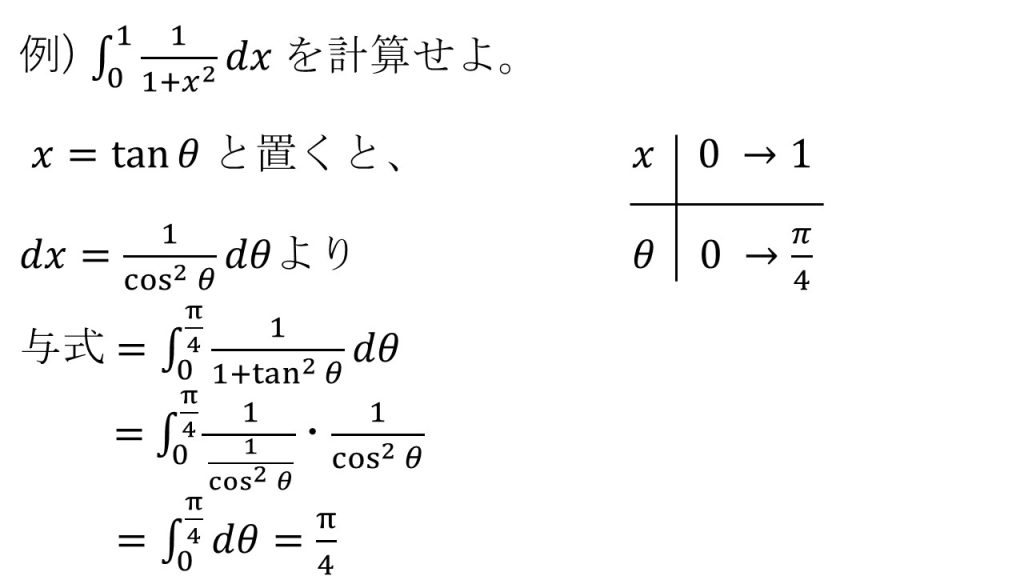
⑨偶関数の定積分
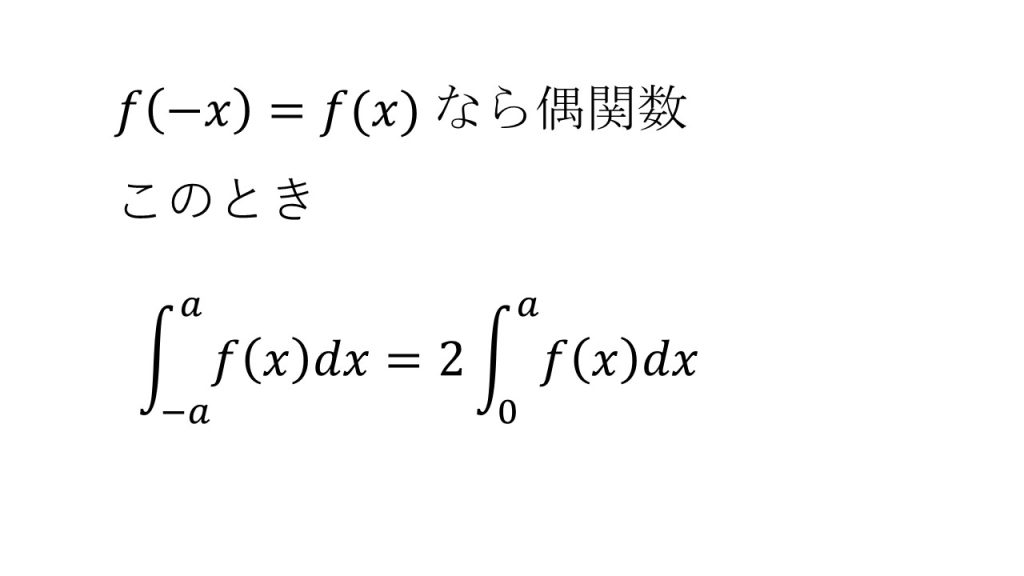
⑩奇関数の定積分

(8)積分法の応用
①区分求積法
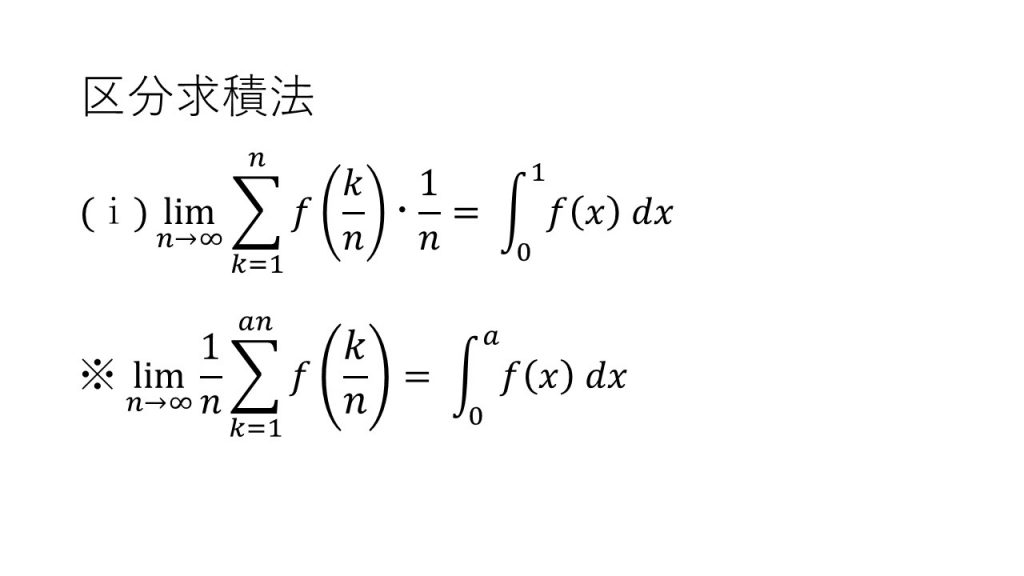
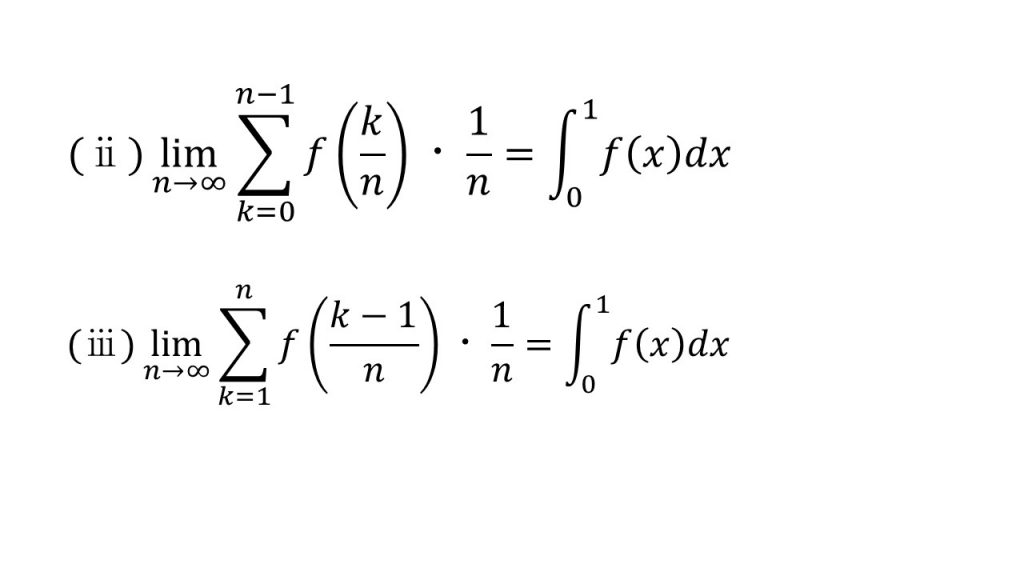
②定積分で表された関数の微分
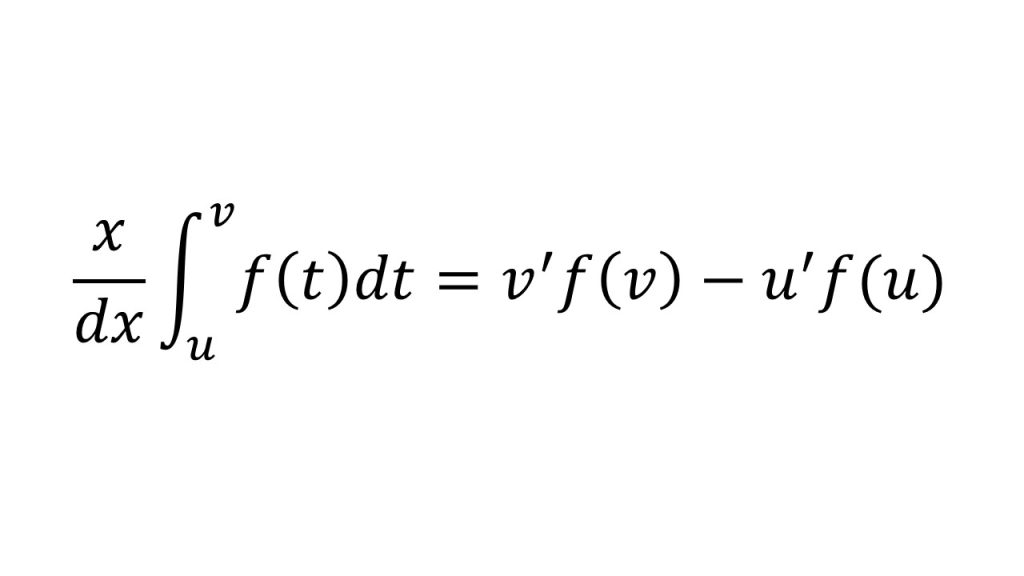
③体積

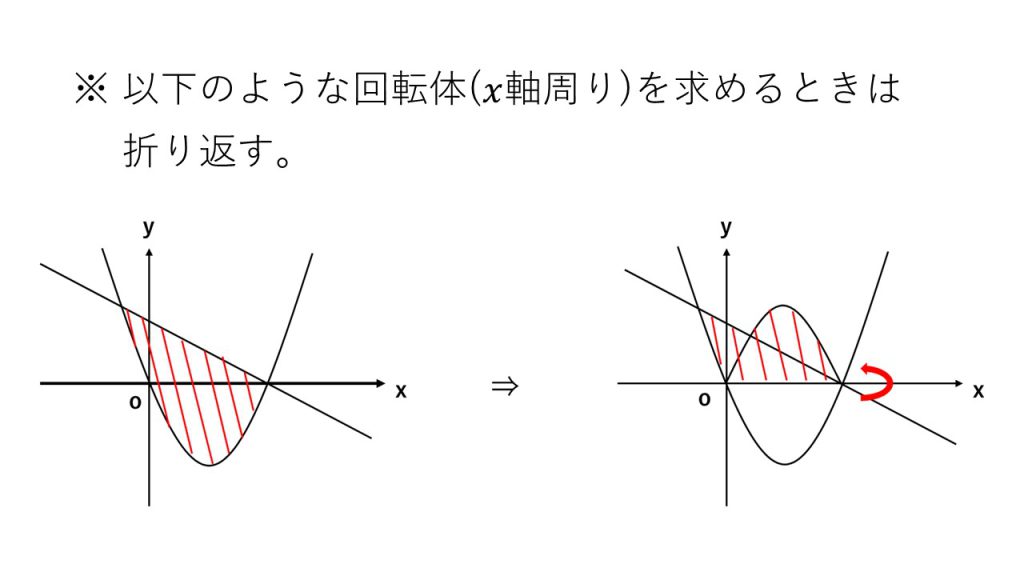
④回転体の体積
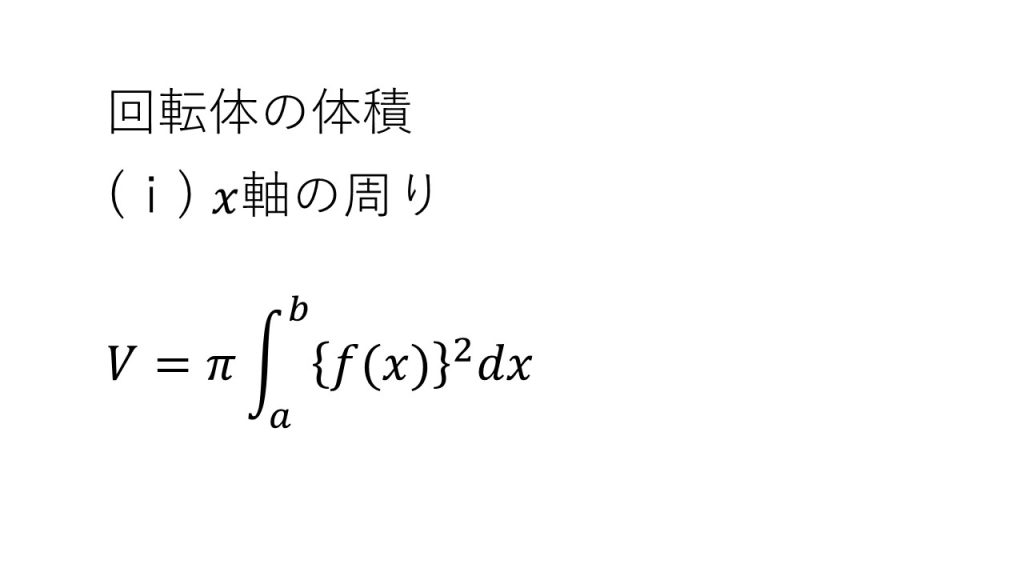
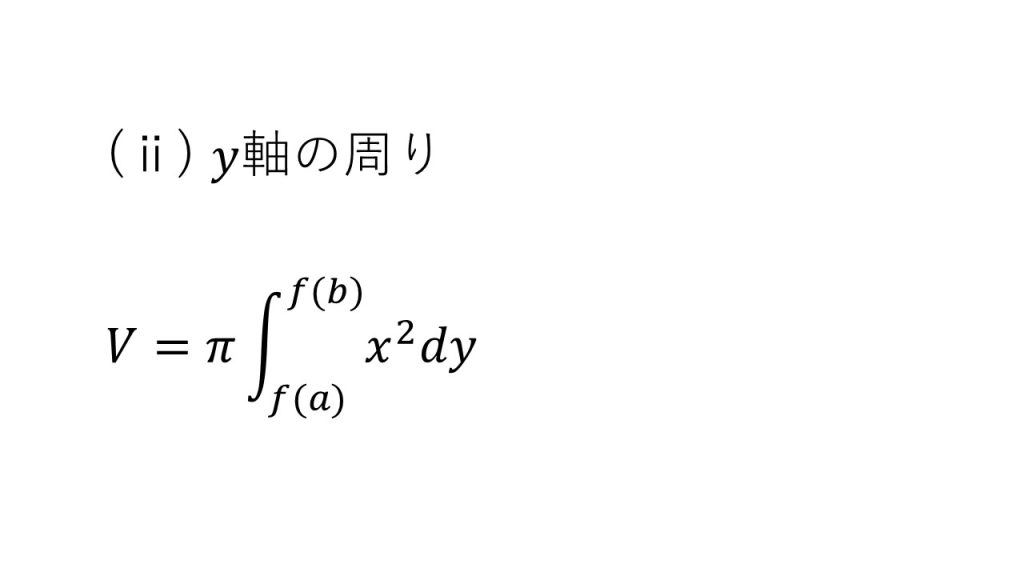

⑤道のり

