(1)例題

(2)例題の答案

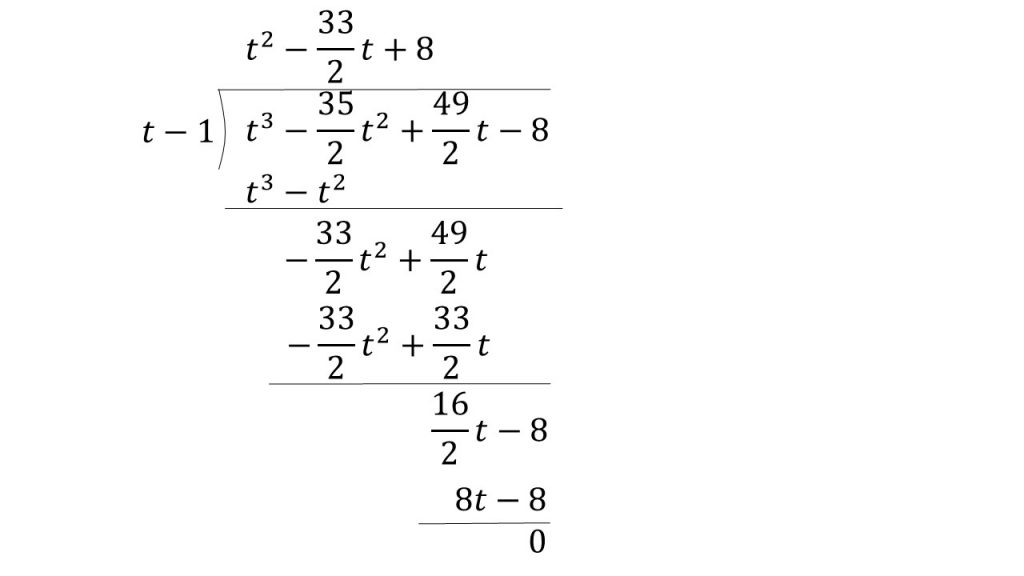
(3)解法のポイント
3次方程式にも解と係数の関係はあります。
ax³+bx²+cx+d=0の解をα、β、γとすると、
α+β+γ=-b/a、αβ+βγ₊γα=c/a、αβγ=-d/a
となります。
ただし、これは覚える必要はなく、
ax³+bx²+cx+d=a(x-α)(x-β)(x-γ)
となり、右辺を展開して整理すれば、
ax³+bx²+cx+d=ax³-(α+β+γ)x²+(αβ+βγ₊γα)x-αβγ
となるので、ここから解と係数の関係を導くことができます。
同様にすれば、何次式の解と係数の関係でも導くことができます。
(4)必要な知識
①解と係数の関係

②因数定理
→1次式x-aが整式P(x)の因数である⇔P(a)=0

(5)理解すべきこと
解と係数の関係の証明ができるようになりましょう→解と係数の関係の証明(三次方程式の解と係数の関係も解説しています)
☆動画はこちら↓
