(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
内分または外分の形にムリヤリ変形する
ベクトルの問題で点がどの位置にあるかを問われたら、やるべきことはベクトルの式を内分または外分の形に無理やりするということです。
この式変形をすることで点がどの位置にあるかを知ることができます。
例題①:平面内の点の位置の問題
実際にやってみましょう。

この点Pはどの位置にあるかを求めてみましょう。
まずはこの式を内分または外分の形にします。内分または外分の形とは以下のような形のことです。
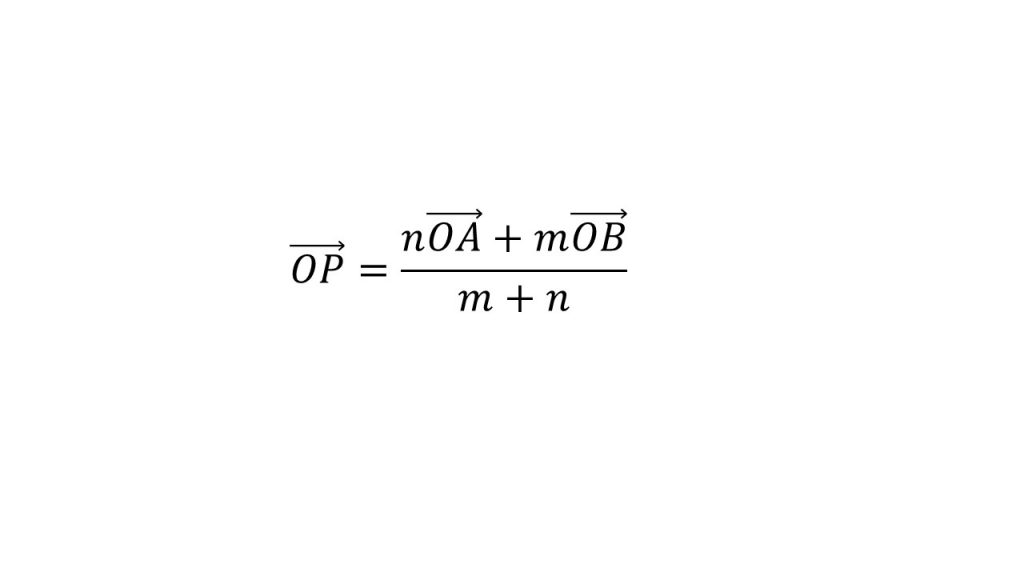
ポイントはOAとOBの係数の和が分母にくるということです。
この形をつくるために、まずOAとOBの係数の分子に注目します。今回は6と3なので6+3=9がOAとOBの係数の分母にくるようにします。そしてイコールが成り立つように9/13をかけて、つじつまを合わせます。そして約分してまとめると以下のようになり、
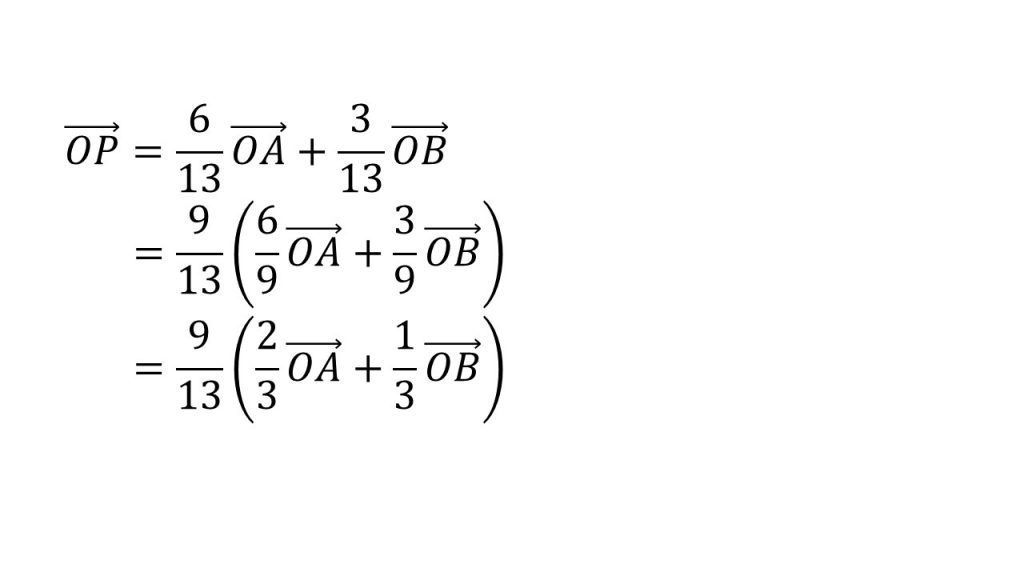
これで内分の公式の形になったので点Pの位置が分かります。すなわち
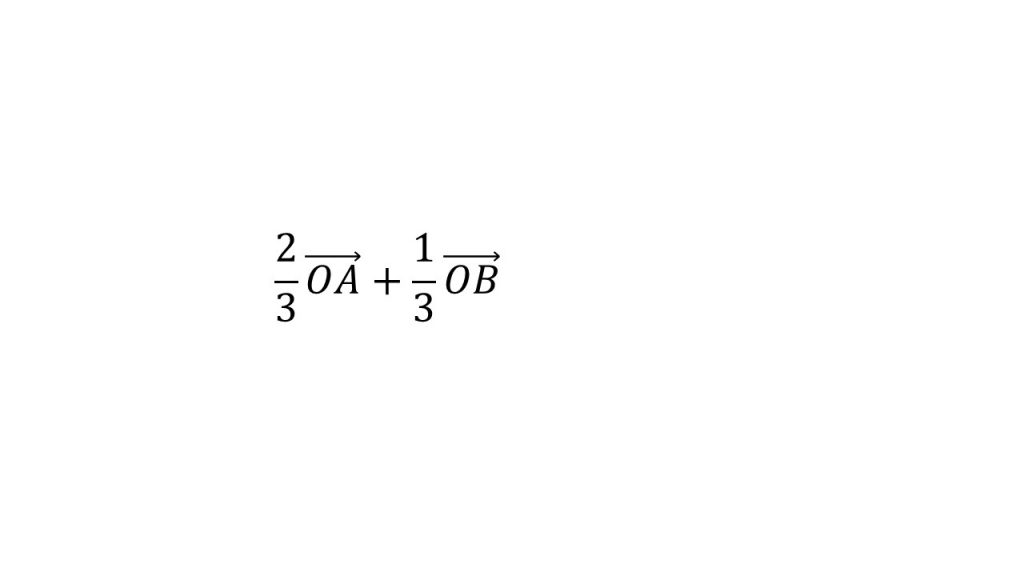
この部分が意味することは線分ABを1:2に内分する点ということを意味しています。2:1ではなく1:2であることに注意してください。
そしてさらに、この部分を9/13倍しているので、
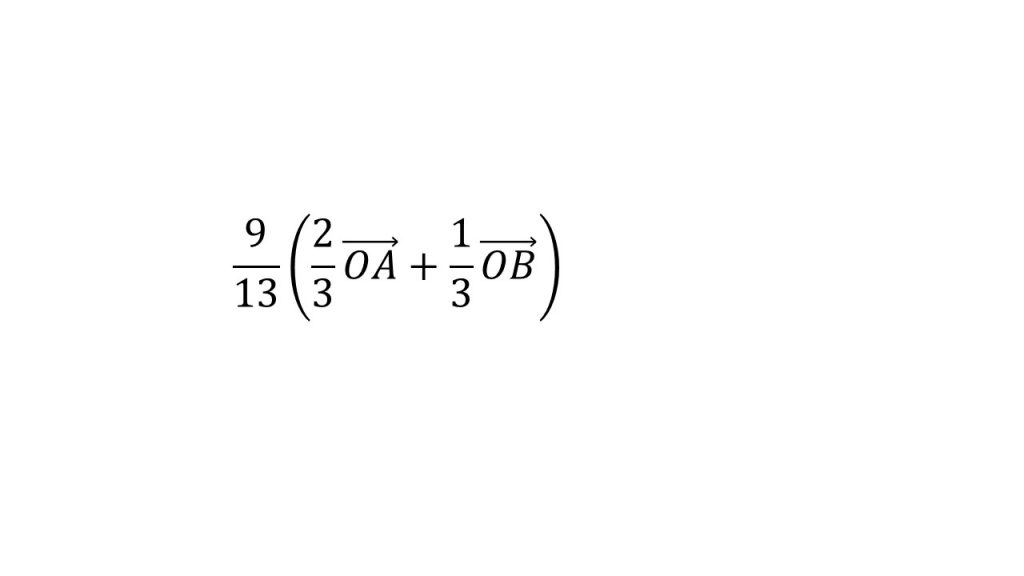
9:4に内分しているということを意味しています。
ゆえに、この式から、点Pの位置は線分ABを1:2に内分する点をQとすると、点PはOQを9:4に内分する点となります。図にすると下図のようになります。
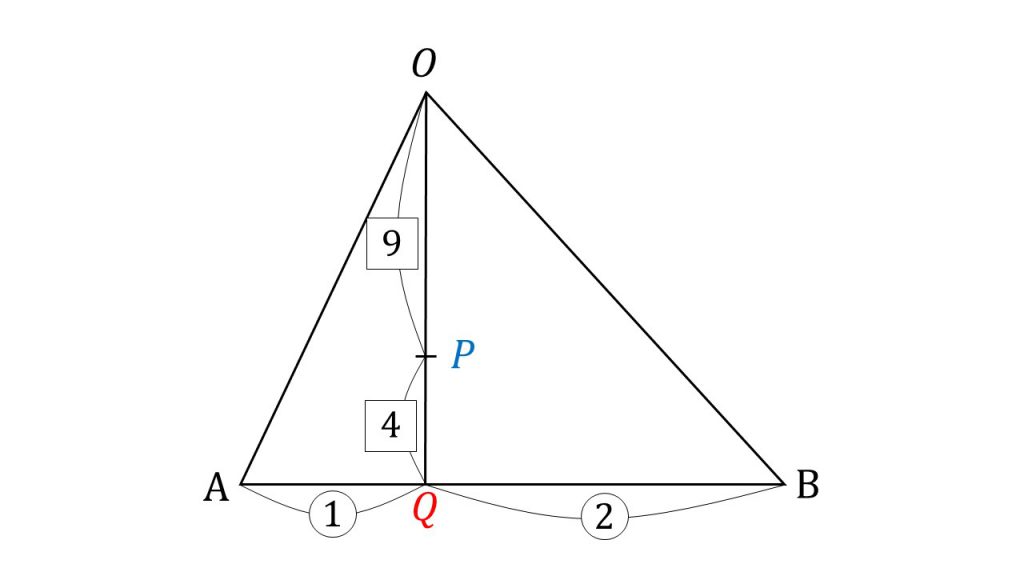
このように、内分または外分の形を作り、その係数を読み取ることで点の位置が分かります。
例題②:空間内の点の位置の問題
それでは空間でも同様の手順で点Pの位置を求めてみましょう。

このような式から点Pの位置を求めるタイプの問題も多いので、今回は、そのタイプの問題でも解いてみます。
始点をそろえる
まず、このように始点がそろっていないベクトルの式を見たらやるべきことは、始点をそろえることです。今回は始点をAにそろえてみましょう。
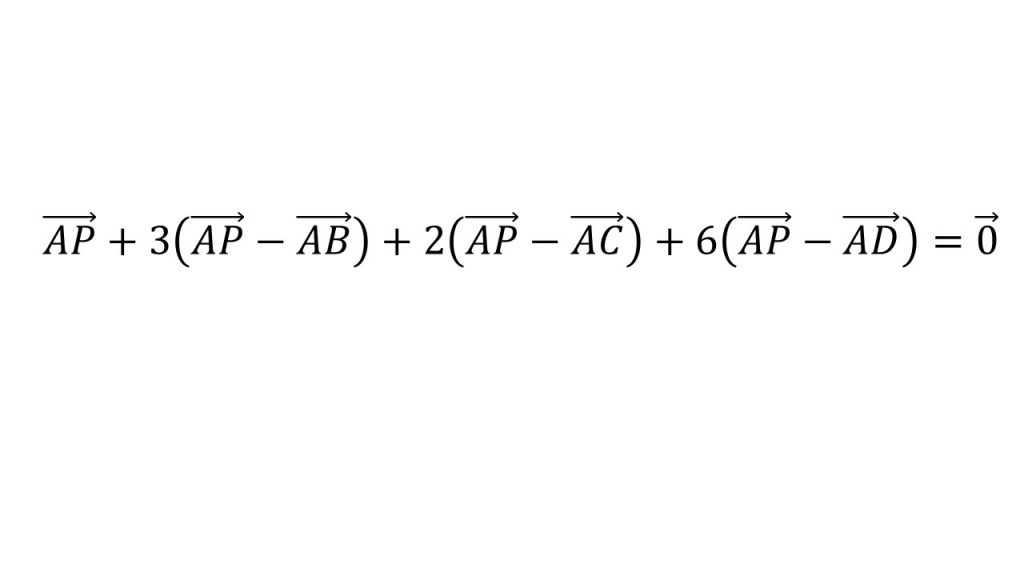
APはそのままで、BPはAP-ABとします。始点のそろえ方は「後ろ引く前」で覚えましょう。同様にCPはAP-AC、DPはAP-ADとなります。このように、始点をそろえるという操作はベクトルの問題を解く上で非常に重要なので、必ずできるようにしておいてください。
それでは始点をそろえ終わったら、今回は点Pの位置を知りたいので、左辺をAPだけの形にします。

内分または外分の形にムリヤリ変形する(2回)
そしてここから先ほどと同様に、内分または外分の形に無理やり変形して行きます。
しかし空間なのでベクトルが3つ出てきます。こういった場合はまず2つを内分または外分の形にします。
ABの係数とACの係数を見て、今回は3と2なので、3+2=5が分母にくるようにします。そして、つじつまを合わせるために5をかけます。
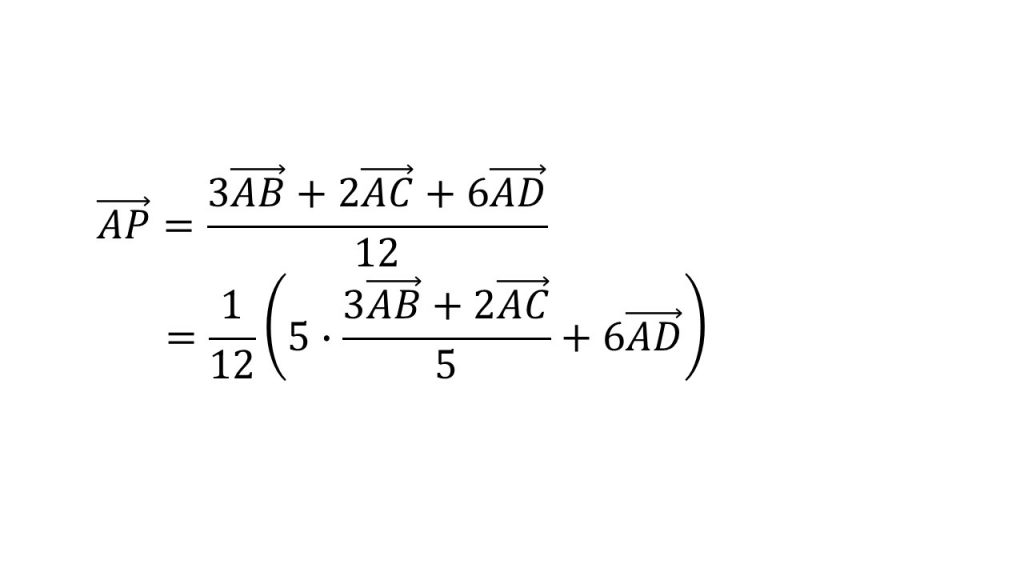
次に、変形した部分をAEなどでおきます。すると以下のようになります。
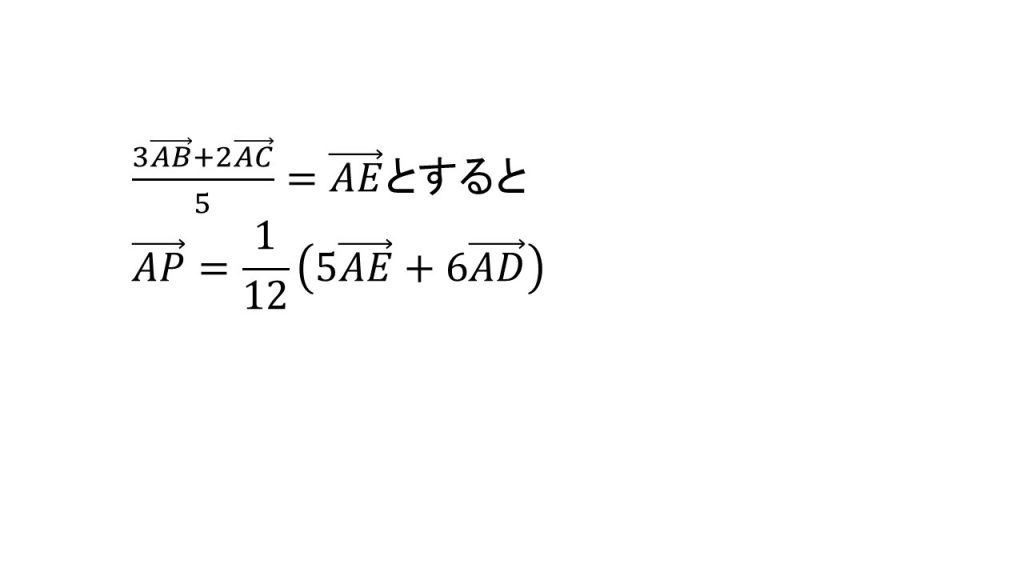
これで2つのベクトルとなったので、また同様に、AEとADの係数を見て5+6=11が分母に来るように式変形をします。イコールが成り立つように11でかけるのを忘れないようにしましょう。
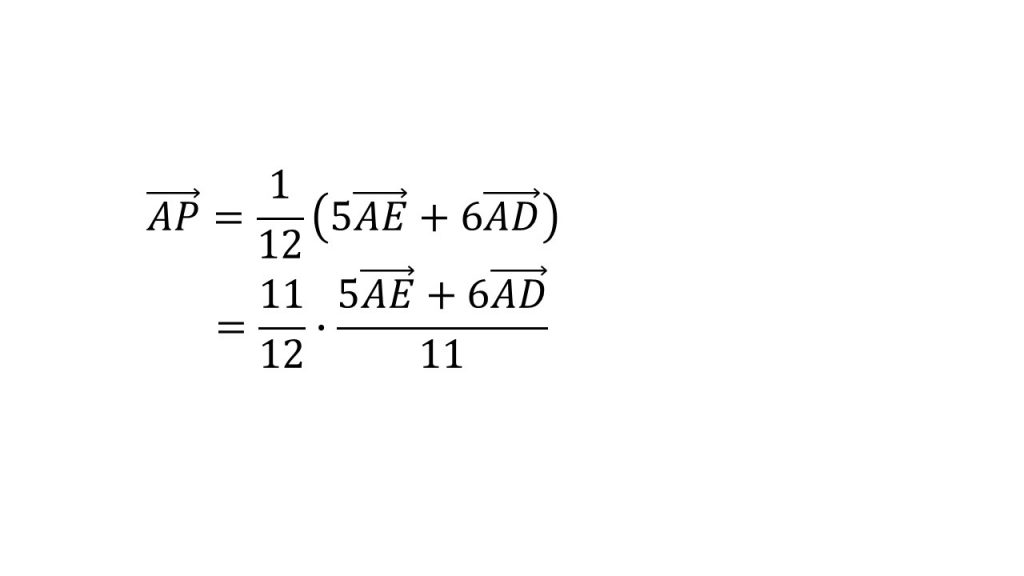
このような形になればもう点Pの位置は分かります。点Pの位置は、線分BCを2:3に内分する点をEとしたとき、線分EDを6:5に内分する点をFとすると、点Pは線分AFを11:1に内分する位置にあるということがわかります。
図でかいてみると下図のようになります。

このように空間でも内分または外分の形に変形することで、点の位置を知ることができます。
(3)解説授業の内容を復習しよう
(4)ベクトル(数学B)の解説一覧
④ベクトルにおける点の位置の問題の解法(内分または外分の公式の形にする、平面ベクトルと空間ベクトルの両方で解説しています)
