(1)例題
「(45°の内角は一つもない)ならば(三つの内角がすべて異なる、または、直角三角形ではない)」という命題の逆と裏と対偶を答え、対偶の真偽を考えた上で、元の命題の真偽を答えよ。
(2013年センター試験本試数学ⅠA第1問〔2〕より)
(2)例題の答案
逆:「(三つの内角がすべて異なる、または、直角三角形ではない)ならば(45°の内角は一つもない)」
裏:「(45°の内角が少なくとも一つはある)ならば(三つの内角のうち等しいものがある、かつ、直角三角形である)」
対偶:「(三つの内角のうち等しいものがある、かつ、直角三角形である)ならば(45°の内角が少なくとも一つはある)」
三つの内角のうち等しいものがある、かつ、直角三角形である三角形は、直角二等辺三角形のことである。よって、対偶は真。
したがって、元の命題は真となる。
(3)解法のポイント
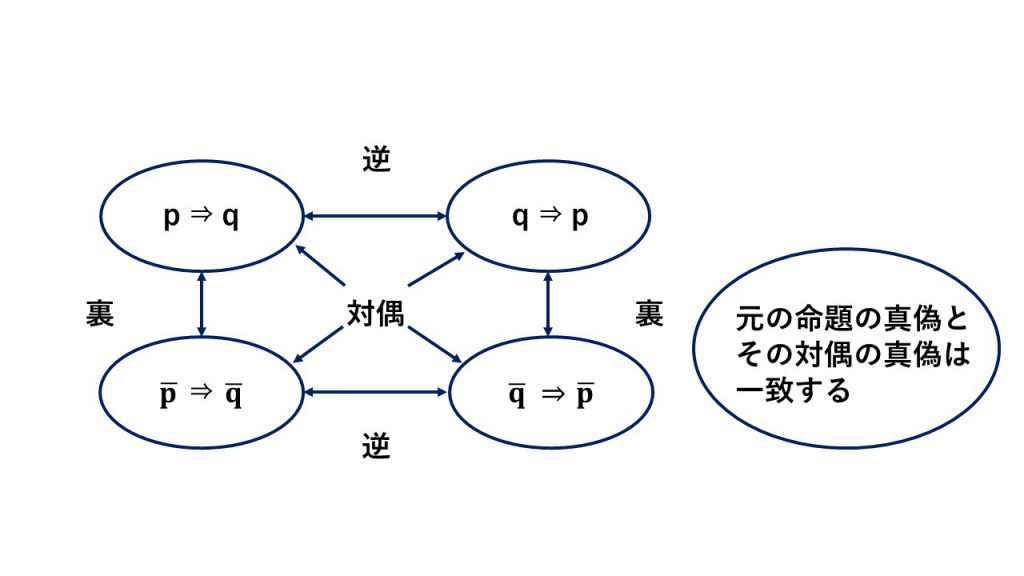
対偶の真偽は、元の命題の真偽は一致することに注意しましょう。ただし、逆と裏の真偽は一致することもしないこともあります。
(4)必要な知識
①対偶