(1)解説授業動画
☆YouTubeチャンネルの登録をよろしくお願いします→大学受験の王道チャンネル
(2)解説授業の原稿
今回は浸透圧について解説します。
浸透圧とは何か
まずはそもそも浸透とは何かについて確認します。
浸透とは半透膜を通って溶媒が溶液に侵入する現象のことです。半透膜とは溶媒は通すけど溶質は通さない膜のことです。
なぜこのような現象が起きるのかというと、溶液には濃度を均一にしようとする性質があるため、このような現象が起きるのです。
例えば、以下のように濃度の違う水溶液を半透膜で隔てると何が起きるのでしょうか。
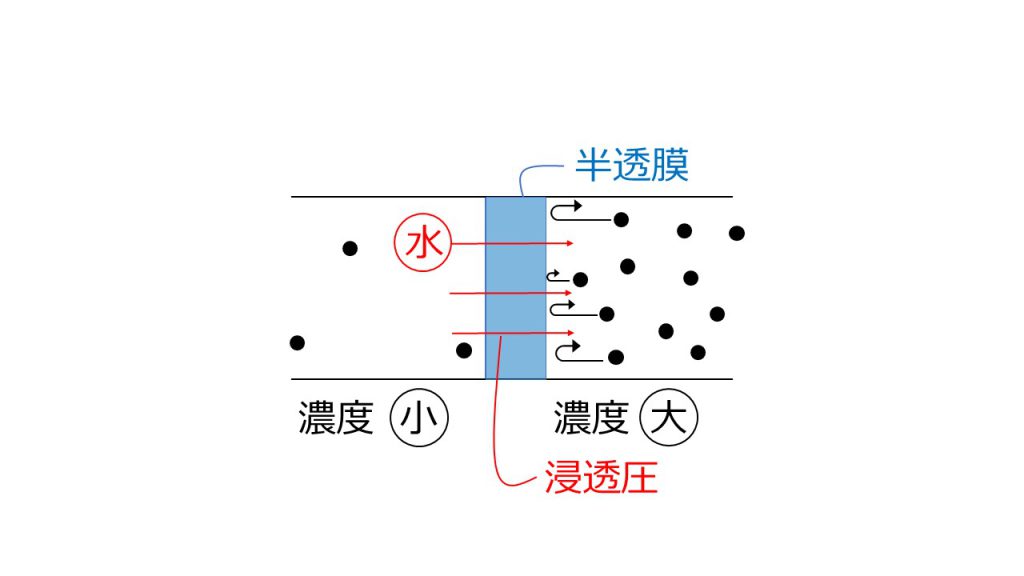
この2つの溶液の濃度を均一にするためには、溶質が左側に移動するか、溶媒が右側に移動するかのどちらかです。
半透膜は溶質を通さないので、濃度が大きい方から濃度が小さい方へ、溶質が移動することができません。しかし半透膜は溶媒を通すので、水などの溶媒は濃度が小さい方から濃度の大きい方へ移動することができます。
これが浸透という現象です。
こうすることによって、左側は溶媒の量が減っていき、濃度が大きくなります。それに対して右側は溶媒の量が増えていくので、濃度は小さくなります。
そしてこのとき半透膜にかかっている圧力のことを、浸透圧というのです。
浸透圧の計算公式
それでは次に計算公式を確認します。浸透圧の計算公式として、教科書などにまず書いてあるのは、
π=cRT
πは浸透圧で単位はPaです。cは溶液のモル濃度で単位はmol/Lです。そしてRは気体定数で、Tは絶対温度で単位はKです。
ただ実際の計算問題を解くときは、こちらの式よりも以下の式のほうが使いやすいと思います。
πV=nRT
Vは溶液の体積で単位はL、nは溶質の物質量で単位はmolとなります。
こちらの式は、π=cRTのcをn/Vとして両辺をV倍したものになっています。cはモル濃度なのでmol/L、つまり溶質の物質量/溶液の体積なので、c=n/Vが成り立ちます。
浸透圧の計算の問題で、モル濃度が直接与えられていることは少なく、基本的に自分で溶質の物質量を求めないといけないので、計算問題を解くときはπV=nRTの公式を使うようにしましょう。
浸透圧の計算で用いる物質量の注意点
また、この公式のnについて注意しないといけないことがあります。
nは溶質の物質量ですが、このときの溶質は分子やイオンなど粒子であればなんでもよい、ということに注意しましょう。
特に電解質を溶かして溶液としたときの、電離した後のイオンを計算に入れるのを忘れないようにしましょう。
この点については凝固点降下や沸点上昇のときと同じです。希薄溶液を考えるときは、溶質に注意する、ということは常に意識するようにしましょう。
なぜ浸透圧の式は理想気体の状態方程式と同じ式になるのか
浸透圧の計算公式が確認できたわけですが、この式を見たときにおそらく多くの人が、ある疑問を抱いたと思います。それは、
「なぜ理想気体の状態方程式と同じ式になるのか」
という疑問が浮かんできたと思います。この疑問に対する答えを一言でいうと、
「希薄溶液だから」
となります。ではなぜ希薄溶液だと理想気体の状態方程式と浸透圧の式が、同じになるのでしょうか。
希薄溶液とは何か
そもそも希薄溶液とは、薄い溶液つまり濃度が小さい溶液のことです。
例えば下図のように多量の溶媒の中に、少量の溶質がポツリポツリとある状態が希薄溶液です。
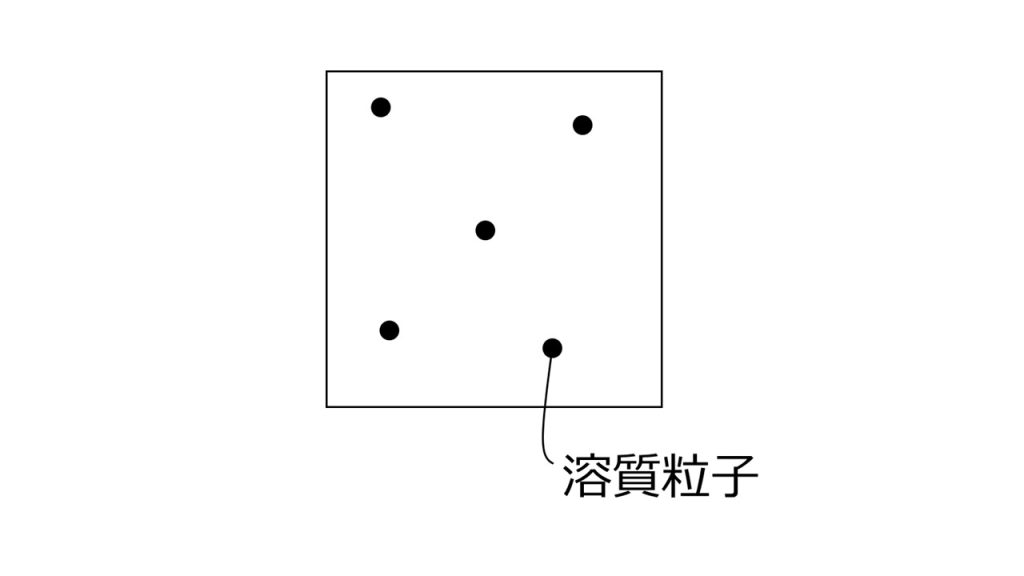
そしてこのような希薄溶液であれば、分子間力など溶質どうしの相互作用はないものとして考えることができ、また溶媒の量に対して溶質の量がとても少ないので、溶質自体の大きさや体積を無視することができます。
こういった条件のもとであれば、πV=nRTの浸透圧の式は、かなり正確に成り立ちます。逆にこういった条件を満たさないのであれば、この関係が厳密には成り立たなくなってしまいます。
希薄溶液と理想気体は同じ状況である
そして、この条件は理想気体の条件と同じである、ということに気づいたでしょうか。
下図のように、理想気体も広い空間の中に気体分子がポツリポツリと存在する気体で、気体分子どうしの分子間力や相互作用を無視し、気体分子自体の大きさや体積を無視した気体のことです。
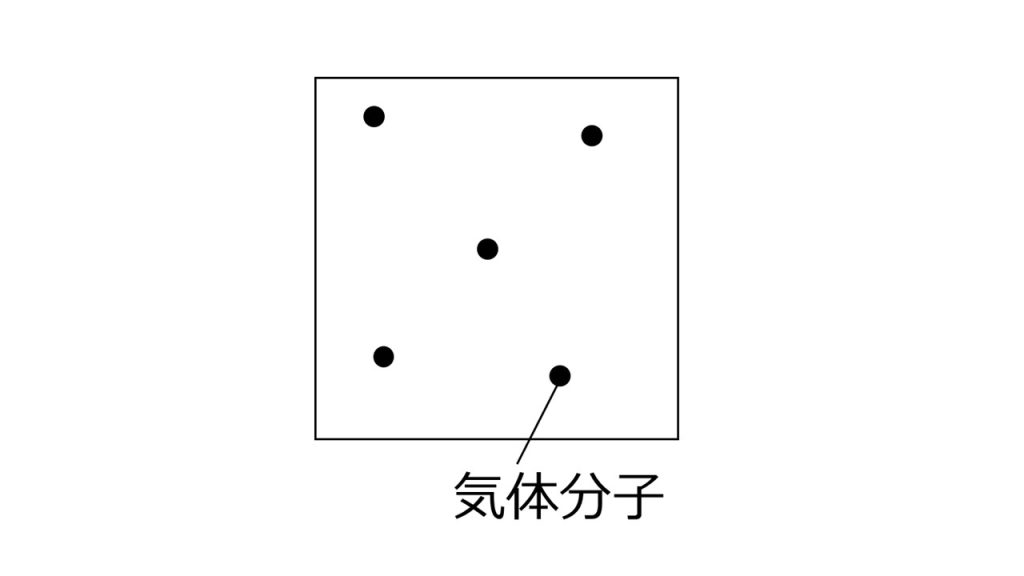
このような条件をみたした理想気体は、pV=nRTの状態方程式が正確に成り立ちます。
このように希薄溶液と理想気体は同じ状況をつくっています。
希薄溶液の浸透圧と理想気体の圧力は同じモデルで考えられる
そして、気体の圧力とは気体分子が壁にぶつかっていく力のことでした。
それと同様に希薄溶液の浸透圧は、溶質粒子が半透膜にぶつかってきているとイメージすることができます。
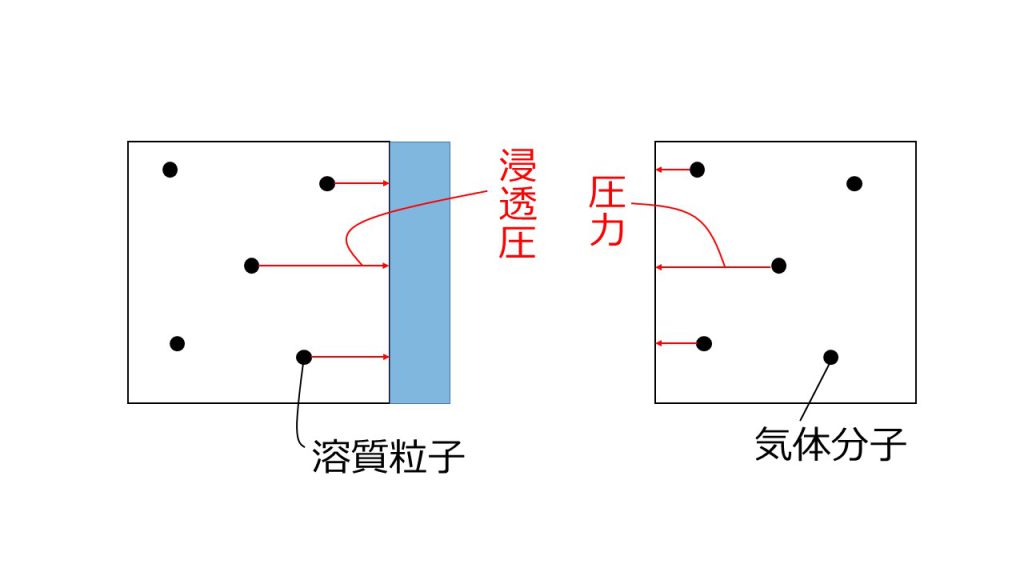
このように理想気体の圧力と希薄溶液の浸透圧は、同じモデルで考えることができるので、浸透圧の式と理想気体の状態方程式は同じ式で表すことができるのです。
希薄溶液と理想気体は同じ状況をつくっており、同じモデルで考えることができるということを知っておくと、希薄溶液をより深く理解することができます。
浸透圧を扱った例題
それでは浸透圧をつかった問題を解いてみます。
ショ糖2.00gを水に溶かして、500㎤とした溶液の浸透圧を下図のような装置を使って調べた。
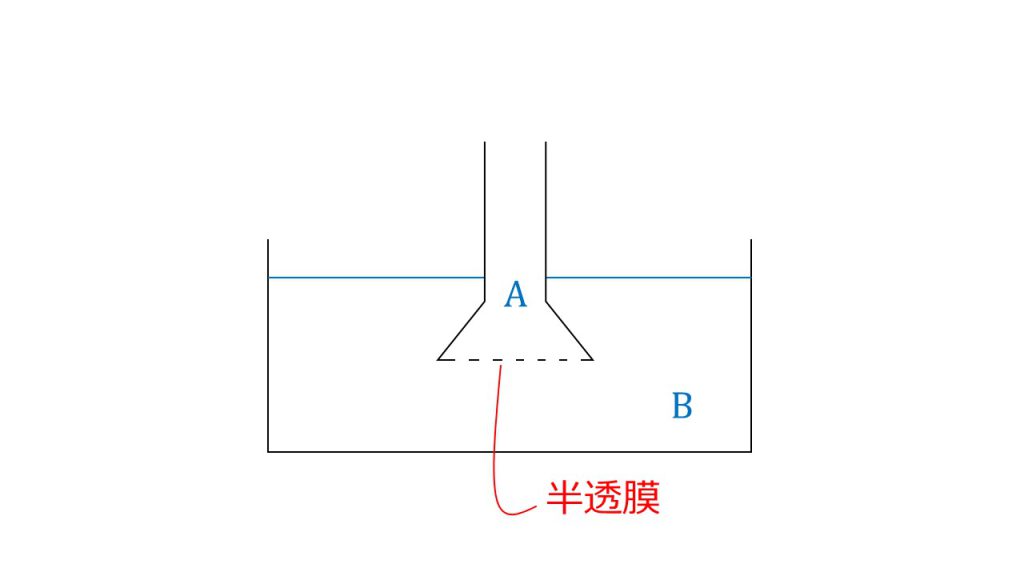
このような問題設定に対して2つの小問があります。
- ショ糖の水溶液はa, bのどちらでしょうか。ただし、他方は純水であるとします。
- 25℃における浸透圧が285hPaのとき、ショ糖の分子量を求めてみましょう。
これらの問題を解いていきます。
小問①:溶液はどちらか
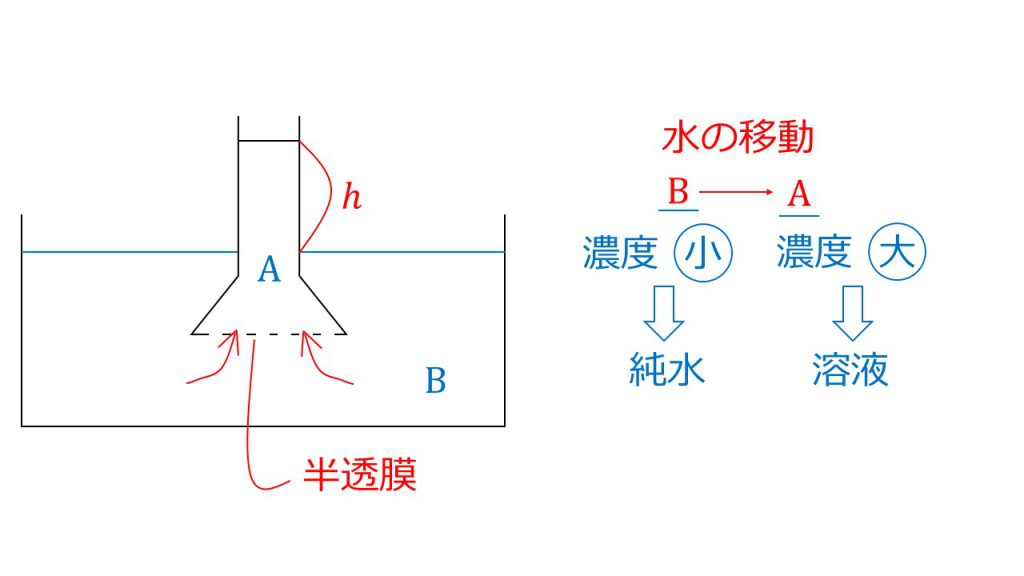
まずは1問目です。先に答えを言うと、答えはaです。
ではなぜaの溶液にしてbを純水とするのでしょうか。
この装置において浸透圧を測るときは、aのガラス管の液面がどれぐらい高くなったかを測定して浸透圧を測ります。
そのため、bからaに溶媒である水が移動しないといけません。浸透は濃度が小さい方から濃度の大きい方に起こるので、aを純水、bをショ糖の溶液とします。
小問②:浸透圧を使って分子量を求める
それでは計算問題を解いてみます。
もう一度問題を確認すると、25℃における浸透圧が285hPaのときショ糖の分子量を求めてみます。ただし答えは整数で答えます。また気体定数の値は8.3×103とします。
方程式を立てる
まずは求めるショ糖の分子量をMとして、この浸透圧の式をつかって方程式を立てていきます。
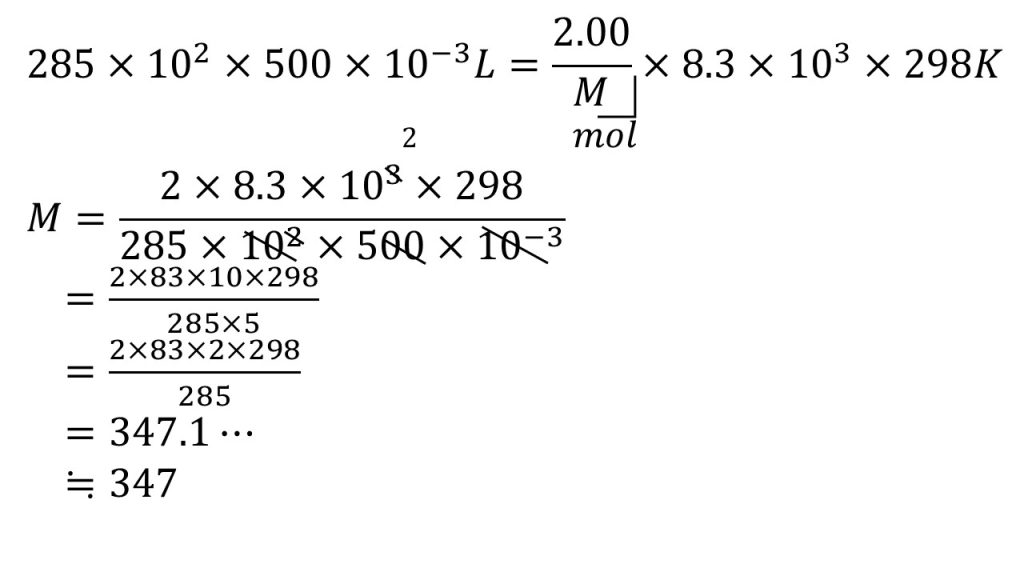
1hPaは100Paのことなので、h(ヘクト)とは102のことです。よって285hPaは285×102Paで、500㎤は500mLのことなので、Lにするために10-3をかけます。
そして、ショ糖の質量をショ糖のモル質量で割ることでショ糖のモルとなり、ショ糖は非電解質(電離しない)なので、これがそのまま溶質のモルとなります。
そして気体定数を代入し、25℃は273を足して398Kとします。
工夫しながら方程式を解く
これで方程式ができたのであとは計算していきます。
方程式を計算するときはまず、求めたい文字だけを左辺にし、残りを右辺に集めます。
そして約分できるだけ約分していきます。まずは分母の10-3を使って、100倍と10を1つ消します。そして10で約分して、これ以上約分できそうにないので、分母と分子をそれぞれ掛け算して、最後に割り算をして、整数になるように四捨五入をして、答えは347となります。
分子量や原子量を答えるときは、単位を書かないように注意しましょう。
いかがだったでしょうか。浸透圧の計算自体は公式を使えばいいので、そこまで難しくはありません。ただ、気体定数が式に入ってくる場合は、計算がややこしくなりやすいので、なるべく工夫して少し楽になるように計算しましょう。
(3)解説授業の内容を復習しよう
(4)希薄溶液(凝固点降下、沸点上昇、浸透圧)の解説一覧
①凝固点降下・沸点上昇(なぜ質量モル濃度の分母が溶媒なのか、計算における注意点についても解説しています)
④浸透圧の解説(なぜ浸透圧の式と理想気体の状態方程式が同じ式になるのかについても解説しています)
☆おまけ:希薄溶液と気体の類似性(ファント・ホッフ「第1回ノーベル化学賞受賞記念講演」より抜粋)
(5)参考
☆化学の解説動画・授業動画一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学知識テスト一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の解説・授業・知識・演習問題一覧(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
☆化学の語呂合わせ(化学基礎・理論化学・無機化学・有機化学・高分子化合物)
「化学計算の王道」シリーズは『思考訓練の場としての体系化学』(GHS予備校)を参考にしています。
GHS予備校についてはこちら→https://ghs-yobikou.co.jp/
思考訓練シリーズの購入はこちら→https://ghs-yobikou.shop/
