(1)例題
ばね定数kの軽いばねの一端に質量mの小物体を取り付け、あらい水平面上に置き、ばねの他端を壁に取り付けた。図のようにx軸をとり、ばねが自然の長さのときの小物体の位置を原点Oとする。ただし、重力加速度の大きさをg、小物体と水平面の間の静止摩擦係数をμ、動摩擦係数をμ’とする。また、小物体はx軸方向にのみ運動するものとする。
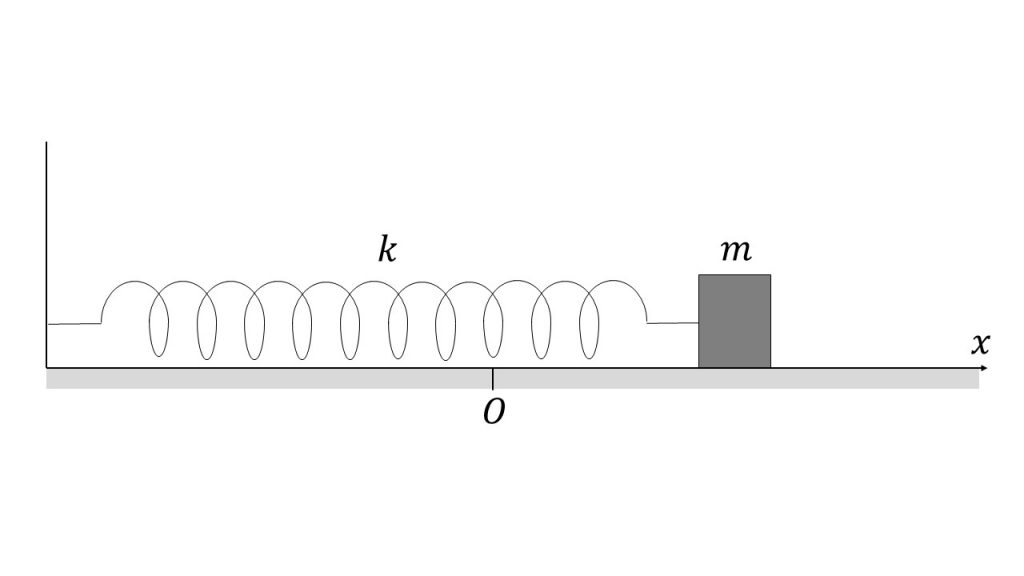
①小物体を位置xで静かに放したとき、小物体が静止したままであるような位置xの最大値xMを表せ。
②xMより右側で小物体を静かに放すと、小物体は動き始め、次に速度が0となったのは時間t1が経過したときであった。この間に、小物体にはたらく力の水平成分Fを、小物体の位置をxとして表せ。またt1を求めよ。
(2018年センター試験本試物理第4問Aより)
(2)例題の答案
①
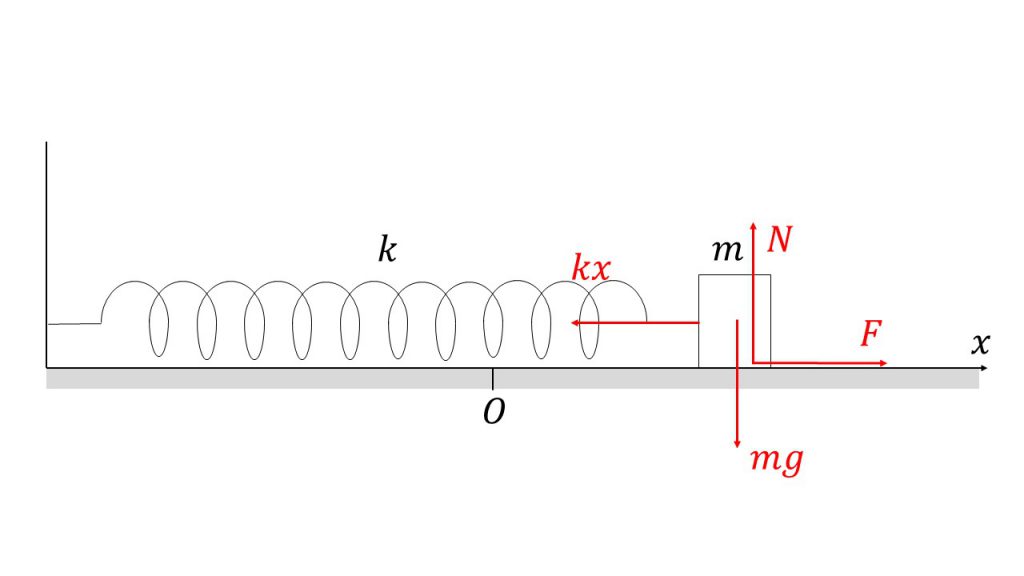

②
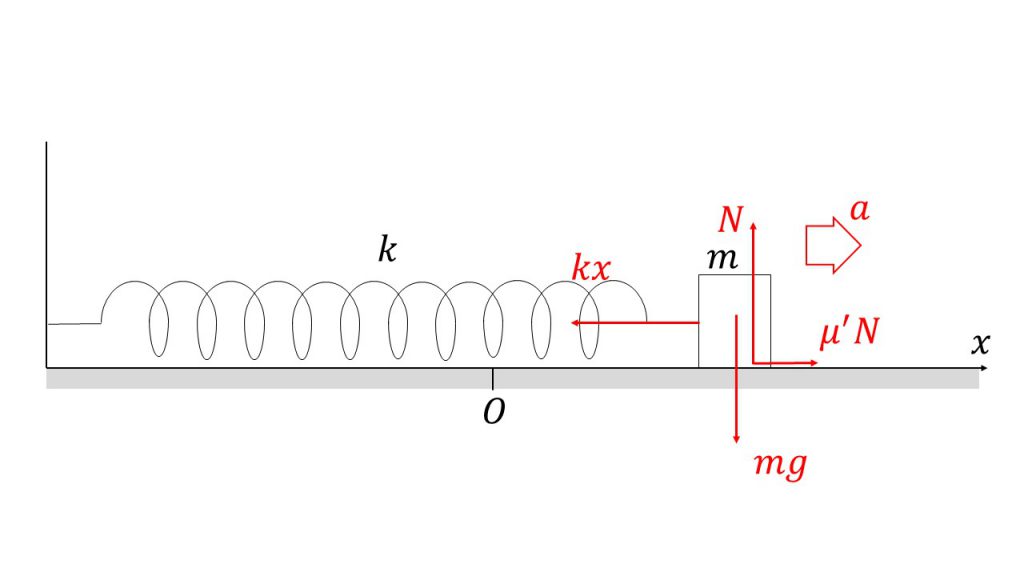


(3)解法のポイント
①静止摩擦力は垂直抗力に比例しませんが、最大摩擦力は垂直抗力に比例します。まずは、このことを理解してください(静止摩擦力が垂直抗力に比例すると勘違いしている人が多いです)
②単振動の問題はとにかく、a=-ω2(x-x0)の形を作りましょう。そうすれば周期が分かります。
あとは、単振動のどの位置で速度が0か、あるいは最大かといった基本知識をおさえておきましょう。
(4)必要な知識
①最大(静止)摩擦力

②動摩擦力

③単振動の角振動数

④単振動の加速度

⑤単振動を考えるときのポイント
ⅰ)振動の中心では速さが最大、加速度の大きさは0
※振動の中心は力のつり合いの位置
ⅱ)振動の両端では速さは0、加速度の大きさは最大
※手を離した位置が振動の端となる。
(5)理解すべきこと
単振動の速度と加速度を微分を使って導く方法の解説→単振動の速度と加速度を微分で導く(合成関数の微分を使っています)
☆動画はこちら↓
(6)参考
☆単振動の勉強法はこちら→単振動
☆力学の勉強法はこちら→力学の勉強法
