(1)例題

(2)例題の答案
①基本

②x²の係数が分数の場合

③x²の係数が負の数の場合
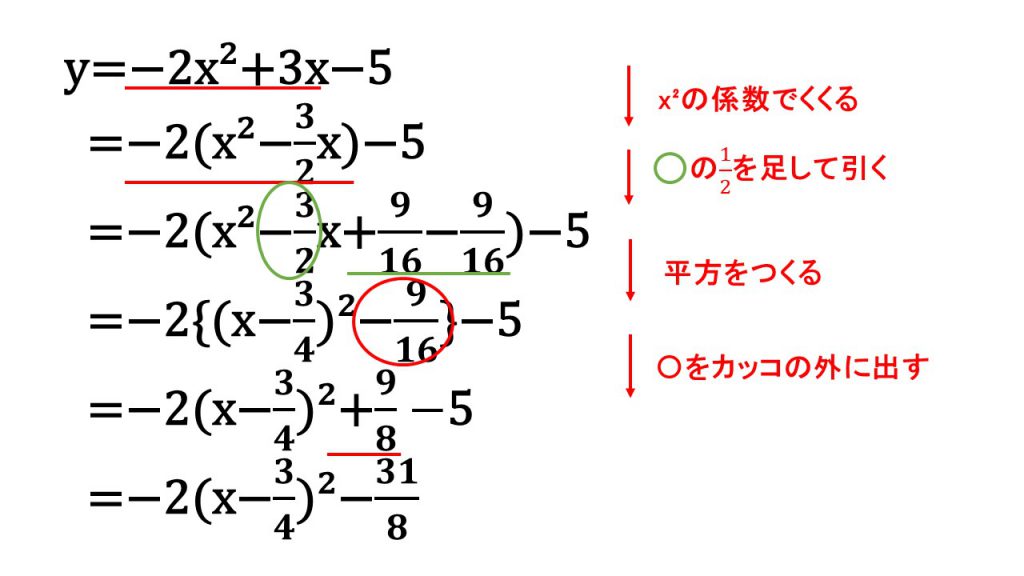
(3)解法のポイント
二次関数のグラフの頂点の座標や軸を求めるためには、平方完成をします。
平方完成は、ミスをしないように検算しながら進めるとよいでしょう。
例えば、

このように展開して元に戻るか確認しながら、進めるとミスなく平方完成ができます。
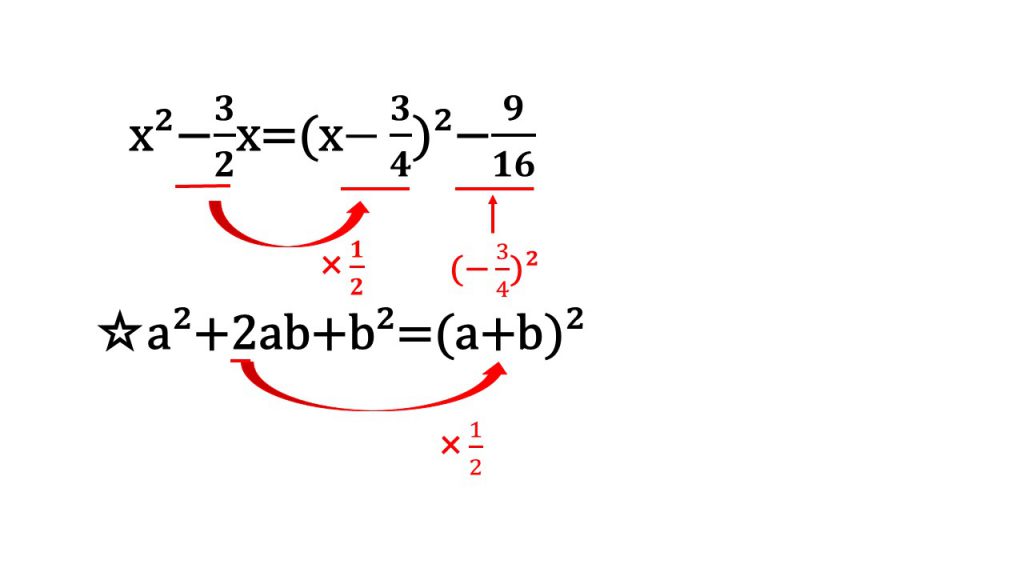
また、平方を作るときは、xの係数の½の2乗を引かないといけないのですが、その理由は、以下の通りです。
(1)例題

(2)例題の答案
①基本

②x²の係数が分数の場合

③x²の係数が負の数の場合

(3)解法のポイント
二次関数のグラフの頂点の座標や軸を求めるためには、平方完成をします。
平方完成は、ミスをしないように検算しながら進めるとよいでしょう。
例えば、

このように展開して元に戻るか確認しながら、進めるとミスなく平方完成ができます。
また、平方を作るときは、xの係数の½の2乗を引かないといけないのですが、その理由は、以下の通りです。
