(1)例題
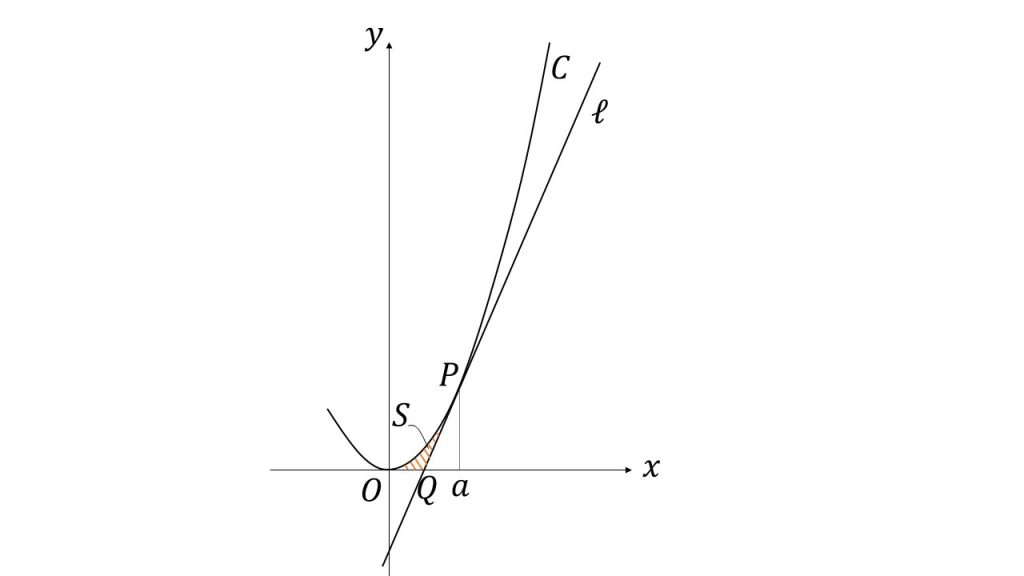
座標平面上で、放物線y=x2をCとする。また、曲線C上の点P(a, a2)における接線ℓの方程式はy=2ax−a2である。ただし、0<a<2であるとする。
①曲線Cと直線ℓおよびx軸で囲まれた図形の面積Sを求めよ。
②曲線Cと直線ℓおよび直線x=2で囲まれた図形の面積Tを求めよ。
(2011年センター試験本試数学ⅡB第2問より)
(2)例題の答案
①

※①積分だけで解く場合

②


※②積分だけで解く場合

(3)解法のポイント
面積を求める場合、必ずしも積分だけで求める必要はありません。
三角形の面積であれば、底辺×高さ÷2
台形の面積であれば、(上底+下底)×高さ÷2
をすればよいのです。
また、三角形や台形を含む図形の面積を求めて、そこから引くという計算をすることで簡単になることがあります。
三角形や台形を見つけたら積極的に工夫して面積を求めましょう。
